Раскрытие скобок

Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.

Чтобы раскрывать скобки, нужно выучить наизусть всего два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и те правила, которые требовалось заучивать наизусть, можно благополучно забыть.

Первое правило раскрытия скобок

Рассмотрим следующее выражение:

Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть, после избавления от скобок значение выражения 8+(−9+3) по прежнему должно быть равно двум.

Первое правило раскрытия скобок выглядит следующим образом:

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Итак, мы видим что в выражении 8+(−9+3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Мы получили выражение без скобок 8−9+3 . Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.

Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

8 + (−9 + 3) = 8 − 9 + 3

Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)

3 + (−1 − 4) = 3 − 1 − 4

Пример 3. Раскрыть скобки в выражении 2 + (−1)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?

В выражении 2−1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2+(−1) . Но если в выражении 2+(−1) раскрыть скобки, то получится изначальное 2−1 .

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть, избавить его от скобок и сделать проще.

Например, упростим выражение 2a+a−5b+b .

Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

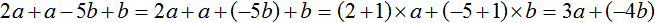
Получили выражение 3a+(−4b) . В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:

Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b .

Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:

Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)

В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:

Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.

На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3. Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4) , нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)

Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:

−5 + (2 − 3) = −5 + 2 − 3

Пример 5. Раскрыть скобки в выражении (−5)

Перед скобки стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)

Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

2a + (−6a + b) = 2a −6a + b

Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)

В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

5a + (−7b + 6c) + 3a + (−2d) = 5a −7b + 6c + 3a − 2d

Второе правило раскрытия скобок

Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

Например, раскроем скобки в следующем выражении

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Мы получили выражение без скобок 5+2+3 . Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.

Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 − (−2 − 3) = 5 + 2 + 3

Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:

6 − (−2 − 5) = 6 + 2 + 5

Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)

Пример 4. Раскрыть скобки в выражении −(−3 + 4)

Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9−2) нужно применить первое правило:

−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2

Пример 6. Раскрыть скобки в выражении −(−a − 1)

Пример 7. Раскрыть скобки в выражении −(4a + 3)

Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:

2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5

Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)

Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:

−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15

Механизм раскрытия скобок

Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:

На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)

3 × (4 + 5) = 3 × 4 + 3 × 5

Поэтому если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.

Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?

Дело в том, что перед любыми скобками стоит общий множитель. В примере 3×(4+5) общий множитель это 3 . А в примере a(b+c) общий множитель это переменная a .

Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1 , в зависимости от того какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1 . Если перед скобками стоит минус, значит общим множителем является −1 .

К примеру, раскроем скобки в выражении −(3b−1) . Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:

Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:

Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.

Для удобства заменим разность, находящуюся в скобках на сумму:

Далее умножаем общий множитель −1 на каждое слагаемое в скобках:

−1 (3b −1) = −1 (3b + (−1)) = −1 × 3b + (−1) × (−1) = −3b + 1

Как и в прошлый раз мы получили выражение −3b+1 . Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:

Но не мешает знать, как эти правила работают.

В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:

Раскрыть скобки и привести подобные слагаемые в следующем выражении:

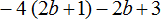
Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:

1) Раскрываем скобки:

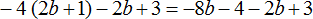
2) Приводим подобные слагаемые:

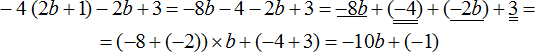
В получившемся выражении −10b+(−1) можно раскрыть скобки:

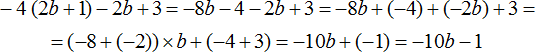
Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:

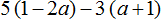
1) Раскроем скобки:

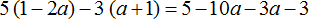
2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть

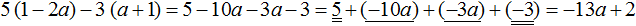
Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4

1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m , можно вынести в нём общий множитель m за скобки:

2) Находим значение выражения m(8+3) при m=−4 . Для этого в выражение m(8+3) вместо переменной m подставляем число −4

m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44

spacemath.xyz

Как раскрывать скобки

Рассмотрим три правила раскрытия скобок: как раскрывать скобки, если перед скобками стоит знак плюс, как раскрывать скобки, когда перед скобками стоит знак минус, и как раскрывать скобки, перед которыми стоит множитель.

1. Если перед скобками стоит знак «+», то знаки в скобках не меняются.

2. Если перед скобками стоит знак «-«, знаки в скобках меняются на противоположные.

3. Если перед скобками стоит множитель, надо этот множитель умножить на каждое слагаемое, стоящее в скобках.

159 Comments

Вашему сайту цены нет, особенно для таких как я. Мы живем в Великобритании, и здесь дети дома свободны от домашних работ в возрасте до 11 лет, я стараюсь выцепить любую информацию в интернете по математике и заниматься с сыном по российской программе. Потому что так как они здесь учатся — это смех один! так вот, сейчас просмотрела Ваш сайт вдоль и поперек и подумала, а можно Вас попросить немножечко прихватить из программы 3-4 класса? А то это для нас еще сложновато))) мы будем заходить и учиться как нормальные дети! Спасибо!!Материал изложен просто прекрасно!

Да,согласен со всеми очень классный сайт.Сейчас щёлкаю математику как семечки:)

Спасибо, Эмиль!
Желаю Вам поддерживать высокий уровень в освоении математики!

ужастный сайт ничего не понятно

Значит, Вам следует поискать более понятное объяснение в другом месте.

Сайт норм. Всё понятно.

Здраствуйте я все понял но есть вопрос 2(x-5)=9 как раскрыть зарание спасибо

2x-10=9. Дальше решаем обычное уравнение.

Ирина, спасибо за теплый отзыв! Первоначально на сайте планировала только материал по 6 классу изложить, потом в качестве повторения добавился 5-й. С младшими школьниками я не работала, поэтому, к сожалению, не смогу Вам помочь в программе 3 класса. Что до 4 класса — в прошлом году занималась с 4-классником, так у них программа во многом совпадает с 5 классом. Постараюсь детализировать повторение 5 класса. Для общего развития ребенка посмотрите здесь: http://www.uznateshe.ru/topics/iq-trening/

Спасибо, хоть вспомнил)

Здравствуйте! Вчера прошли по математике раскрытие скобок, ничего не поняла. В учебнике всё как-то запутанно, да и учитель для меня не понятно объяснил. Забила в поиске «раскрытие скобок». Нашла этот сайт, почитала и всё поняла. Ещё раз,большое спасибо!

Айрис, я рада, что у меня получилось помочь Вам разобраться в этой теме.

Не подскажите,как раскрывать скобки в скобках?Точно так же?

Да, применяем эти же правила.

И мне понравилось, очень доступно. Спасибо)

спасибо, но вы не сказали что нужно сделать если перед скобкой стоит знак .

Антон, не поняла, Вы имеете в виду вопросительный знак? Если так, тогда скобки уже раскрыты, и надо подумать, какое из трех правил раскрытия скобок было применено.

помогите мне пожалуйста раскрыть скобки три примера:
1) (3a-2b+4c)*(-2a)=?
2) 20a-(a-3)+(3a+10)=?
3) 4*(a-2b)-1.5*(4a+5b)=?

1) (3a-2b+4c)*(-2a)=
=3a*(-2a)-2b*(-2a)+4c*(-2a)=
=-6a²+4ab-8ac;
Здесь множитель -2а стоит не перед скобками, а после них, но от перестановки мест множителей произведение не меняется, используем обычное правило раскрытия скобок, перед которыми стоит множитель.
2)20a-(a-3)+(3a+10)=
Перед первыми скобками стоит «-«, поэтому знаки в скобках меняем на противоположные, перед вторыми скобками стоит «+», поэтому знаки в скобках не изменяем:
20a-(a-3)+(3a+10)=
=20a-a+3+3a+10=
=22a+13;
Множители перед скобками умножаем на каждое слагаемое, стоящее в скобках:
3)4*(a-2b)-1.5*(4a+5b)=
=4a-8b-6a-7,5b=
=-2a-15,5b.

Скажите пожалуйста как раскрыть скобки если перед ними нет ничего

Если перед скобками ничего не написано, то по умолчанию, перед ними стоит знак плюс. Соответственно, надо раскрыть скобки, не меняя знаки слагаемых, стоящих в скобках.
Например, (7a-5b+3)-(4a+2b-1)=
Перед первыми скобками стоит знак «+» (хотя он не написан!), знаки в скобках не меняем. Перед вторыми скобками стоит знак «-«, знаки в скобках меняем на противоположные:
=7a-5b+3-4a-2b+1=3a-7b+4.

А если знак [:] как раскрить скобки

Если перед скобками стоит знак «:», а в скобках — сумма или разность, то пример выполняем по действиям. Сначала — действия в скобках, затем — деление.

здравствуйте,ходила на занятия,вроде и поняла, но больше склоняюсь к нет.
так вот если вначале перед скобокой стоит-
то ничего не меняется??
пример; -(a-b+c)
P.s сайт очень помог, большое спасибо)

Извините, отвечаю всем с опозданием.
Если перед скобками стоит знак «минус», все знаки в скобках нужно изменить на противоположные:
-(a-b+c)=-a+b-c. Знаки не меняются, если перед скобками стоит знак «плюс»: +(a-b+c)=a-b+c.

А мне надо раскрыть скобки в примерах:
1) 2*(x-3)
2) (5+a)*4
3) (8-y)*6
4) 3*(12-b)

Если перед скобками стоит множитель, надо умножить этом множитель на каждое слагаемое, стоящее в скобках. От перестановки мест множителей произведение не меняется, поэтому множитель, стоящий после скобок, также умножаем на каждое слагаемое в скобках:
1) 2*(x-3)=2*x-2*3=2x-6;
2) (5+a)*4=5*4+a*4=20+4a;
3) (8-y)*6=8*6-y*6=48-6y;
4) 3*(12-b)=3*12-3*b=36-3b.

А что если и в скобках и во множителе стоит х

Если и в скобках, и в множителе перед скобками стоит х, то действуем по правилу, то есть множитель, стоящий перед скобками, умножаем на каждое слагаемое в скобках. Если число взять множителем два раза, то получим квадрат этого числа: х∙х=х².
Например, 2х∙(5х+3)=2х∙5х+2х∙3=10х²+6х.

у меня перед скобкой стоит минус, а внутри скобки-делениe. деление тоже меняется или нет!?

Если речь идет о выражении вида
a-(b:c-m:n)=a-b:c+m:n,
то здесь каждое из частных b:c и m:n мы рассматриваем как одно слагаемое.

Подскажите пожалуйста, как решить?
Мне надо перемножить скобки, делаю все по правилам, однако ответ не сходится…
(X-25) x (5X-X^2) — (3X+5) x (5X-25)

(x-25) ∙ (5x-x^2) — (3x+5) ∙ (5x-25)=
=x∙(5x-x^2)-25∙(5x-x^2)-3x(5x-25)-5(5x-25)=
=5x^2-x^3-125x+25x^2-15x^2+75x-25x+125=
=-x^3+15x^2-75x+125. Но это уже алгебра ?

спасибо большое!
Да, хотя это и алгебра, а без 6 класса там не обойтись… : )
заваливаешься на таких, вроде бы мелочах, как раскрытие скобок и смена знаков

Светлана, а можно еще вопрос из алгебры, он не по теме, просто я не могу найти в дробях
могу ли я сократить дробь, если в числителе и знаменателе стоит сумма или разность подобных многочленов?

например : 2х-1 / 4х -1

могу я упростить? если нет то что можно сделать?

Нет, сокращать можно только множители.

Извините пожалуйста,не могли бы помочь мне…Как раскрыть скобки,вот в таких примерах:
1.(х-у)+(у-3b)
2.-(а-b)+(-x+a)-(b-x)
3.-(x-9)+(a-5)
4.(a-7)-(5+a)-(9-a)
Заранее спасибо!:)

1.(х-у)+(у-3b)=х-у+у-3b=x-3b;
2.-(а-b)+(-x+a)-(b-x)=-a+b-x+a-b+x=0;
3.-(x-9)+(a-5)=-x+9+a-5=-x+a+4;
4.(a-7)-(5+a)-(9-a)=a-7-5-a=-12.
Полина, здесь правил всего два: если перед скобками «+», знаки в скобках при раскрытии не меняем, если «-» — меняем на противоположные. После чего — приведение подобных слагаемых.

Вы просто молодец, что так трудитесь! От всего честного народа Вам большое-большое спасибо!

Только вот непонятно, куда в первом примере испарился y? х-у+у-3b=x-3b

Спасибо! -у и у — противоположные числа, поэтому их сумма равна нулю: -у+у=0.

Здравствуйте ! Спасибо большое ! Я наконец-то поняла ! Учила правлила , читала , спрашивала у взрослых — никто не мог нормально объяснить ((
Большое спасибо вам

Мария, я рада, что Вы поняли эту тему. В математике очень важно вовремя усвоить каждый новый раздел, ничего не оставляя «на потом». Желаю Вам дальнейших успехов!

Просто прекрасно. Спасибо что вы есть))).

Уважаемая Муза! Ваш эмоциональный отзыв вдохновляет меня на подвиг))

Здравствуйте! Извините пожалуйста,не могли бы Вы мне помочь…Как правильно раскрыть скобки в таких примерах:
(0.15^2 p^2+2*1.17*0.15p+1)(0.5p+1)(1.2p+1)+0.28

Формул здесь нет. Я бы сначала перемножила вторую и третью скобки, а затем первую с тем, что получится.

Если перед двумя скобками стоит знак?
Например 5(x+1)(x-1).

Аналогично. Если перед скобками «+», знаки в скобках не меняются, если «-» — изменяются на противоположные. Во втором случае лучше сначала перемножить выражения в скобках, а уже потом изменить знаки. Например,

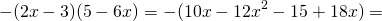
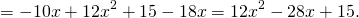
Если перед произведением двух выражений в скобках стоит третий множитель, также удобно сначала перемножить скобки, а затем этот множитель умножить на каждое слагаемое в скобках. Например,

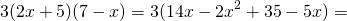
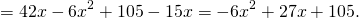
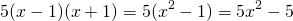
(выражение в скобках равно разности квадратов. Но это уже алгебра)).

Здравствуйте,меня зовут Иосиф у меня по итоговой по математике поставили 2,но дали шанс тому кто 2 получил завтра утром прийти в школу в кабинет математики и переписать контрольную.Так вот я не знал как раскрывать скобки,но когда забил в поисковике «как раскрывать скобки в уравнениях 6 класс» и вот результаты,я зашел на этот сайт и нашел здесь как раскрывать скобки.Спасибо что обьяснили думаю что завтра контрольную напишу на 4.

Иосиф, я желаю Вам написать контрольную завтра на хорошую оценку, а также пересмотреть свое отношение к учебе и стать успешным учеником!

Спасибо,а можете сказать как находить средние и крайние члены пропорции?

Спасибо,пригодится на контрольной.

Помогите,пожалуйста,срочно надо!Сегодня задали очень много дз по матиматике,помогите решить один номер
1)-2(a-2b+1)
2)(2a-3b-4)*3
3)-(5x-2y-10)

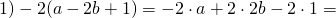
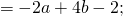
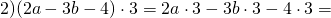
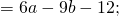
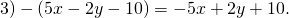
как делить такие скобки?

(4х4-8х2+2)/(х-2)
(числа после «х» это степень, не помню как ставить степень)

Уважаемый студент! Ваш пример — на сокращение алгебраической дроби. Чтобы сократить дробь, надо числитель разложить на множители: сначала вынести общий множитель за скобки, затем выражение в скобках свернуть по формуле квадрата разности. Только Вы что-то с коэффициентами напутали.

А что делать если в скобке выражение и вся скобка находится в отрицательной степени?

Это уже алгебра, степень с отрицательным показателем. Все выражение в скобках уйдёт в знаменатель дроби.

Первым действием выполняется действие в скобках: 9+3=12. Дальше — в порядке очерёдности: 48:2=24; 24∙12=288.

Светлана. А если перед скобкой стоит — без числа что делать? Например: …… -(3+5)+8

Если перед скобками стоит знак «-«, все знаки в скобках нужно изменить на противоположные:-(3+5)+8=-3-5+8 (это как иллюстрация. В данном примере сначала лучше бы сложить 3 и 5).

Помогите :
2,5(3x-2y+4a)
0,12(2a-6b-0,2c)

Если перед скобками стоит множитель, надо умножить этот множитель на каждое слагаемое, стоящее в скобках:
2,5∙(3x-2y+4a)=2,5∙3x-2,5∙2y+2,5∙4a=7,5x-5y+10a;
0,12∙(2a-6b-0,2c)=0,12∙2a-0,12∙6b-0,12∙0,2c=0,24a-0,72b-0,024c.

Помогите решить (х-5)(х+1)=0

Надежда, это уравнение вида «произведение равно нулю«. Посмотрите по ссылке, попробуйте разобраться самостоятельно. Если не получится, спросите еще.

Извините, я не поняла как раскрыть скобки здесь:
(а+1)(а+2).
Объясните пожалуйста.

Это уже алгебра, умножение многочленов:(а+1)(а+2)=a²+2a+a+2

а что делать, если перед скобками отрицательное число

Умножить это число на каждое слагаемое, стоящее в скобках. Так как число отрицательное, знаки слагаемых при этом изменятся на противоположные.

_как решить 33333=27 не повторяя значки

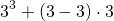
помогите решить уравнение
1,4(3-х)-0,9(х+2)=47

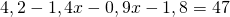
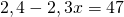
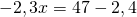
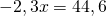
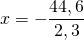
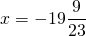
помогите решить уравнение x+(x/1.2)=12.32

Можно обе части уравнения умножить на 1,2, чтобы избавиться от знаменателя:

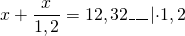
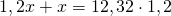
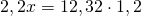
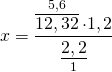
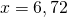
Пожалуйста, помогите разобраться с двойными скобками, а то совсем
запутался. Заранее , спасибо.

3а — ( а — (а — (а — 2b))
4 b + (b — ( a + 3 b))

Здесь возможны варианты. Можно последовательно раскрывать внутренние скобки, можно — внешние. В первом случае получаем:
3а — ( а — (а — (а — 2b)))=3а — ( а — (а — а +2b))=3а — ( а — (2b))=3а — ( а — 2b)=3а — а + 2b=2a+2b.
Во втором случае 3а — ( а — (а — (а — 2b)))=3а — а + (а — (а — 2b))=2a+ (а — (а — 2b))=2a+ а — (а — 2b)=3a-(а — 2b)=
=3a-(а — 2b)=3a-a+2b=2a+2b.
Аналогично: 4 b + (b — ( a + 3 b))=4 b + (b — a — 3 b)=4 b + ( — a — 2 b)=4 b — a + 2 b=6b-a.

Светлана Ивановна, спасибо большое!

Светлана Ивановна, стал решать эти примеры сам и не могу понять , почему во втором примере 4 b + (-a — 2b) при раскрытие скобок получается 4 b — a +2 b, ведь когда плюс перед скобкой, то знаки не меняются или я опять запутался( для меня очень сложна эта тема, все время путаюсь), объясните, пожалуйста

Даниэль, так как в примере 4 b + (-a — 2b) перед скобками стоит знак «+», то при раскрытии скобок каждое слагаемое остаётся с тем же знаком, с которым оно было в скобках, то есть 4 b + (-a — 2b)=4b-a-2b=2b-a.

Помогите пожалуйста решить уравнение с двойными скобками, а то мы никак сами не можем 125-((y-1)+49)=23

Настя, с комментариях уже был пример с двойными скобками. Такие примеры можно решать двумя способами: сначала раскрыть внутренние скобки, затем — внешние, либо наоборот. Но если раскрытие скобок еще не проходили, тогда возможен еще один вариант решения. Чтобы найти неизвестное вычитаемое ((y-1)+49), надо из уменьшаемого вычесть разность:
(y-1)+49=125-23
(y-1)+49=102. Чтобы найти неизвестное слагаемое (y-1), надо из суммы вычесть известное слагаемое:
y-1=102-49
y-1=53. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:
y=53+1
y=54.

как это раскрыть 1/3*(2x+2)

Умножить множитель на каждое слагаемое, стоящее в скобках:
1/3∙(2x+2)=1/3∙2x+1/3∙2=2x/3+2/3.

Не могу понять как автор раскрыл скобки
(r+1)[r(2r+1)+6(r+1)]
Что у него получилось
(r+1)(2r^2+7r+6)

Как придти к этому?

Я тот шаг понял, помогите пожалуйста разобраться с этим, от сюда
(r+1)(2r^2+7r+6)
сюда
(r+1)(r+2)(2r+3)

Светлана Иванова, спасибо большое!

По какой формуле разобраться с этим уравнением?
(7m²-20mn-10m):10m

Илья, уравнения здесь нет. Каждое слагаемое, стоящее в скобках, делим на 10m (но это уже алгебра):
(7m²-20mn-10m):10m=0,7m-2n-1.

Здравствуйте! Помогите пожалуйста решить примеры:
4(3+x); (5x-15)•7; 13•(4+4x-y). Заранее спасибо.

Если перед скобками стоит множитель, надо каждое слагаемое, стоящее в скобках, умножить на этот множитель. Если множитель после скобок — аналогично (от перемены мест множителей произведение не меняется).
4(3+x)=12+4x; (5x-15)•7=35x-105; 13•(4+4x-y)=52+52x-13y.

Помогите пожалуйста раскрыть скобки и упростить выражения, и объясните пожалуйста подробнее
-45-3(9-y)
-6(8-b)+50
-35-5(х+8)
2(3-а)-16
заранее большое спасибо.

Если перед скобками стоит множитель, надо каждое число, стоящее в скобках, умножить на этот множитель. При этом, если множитель со знаком «+», знаки слагаемых в скобках не изменяем. Если же множитель перед скобками со знаком «=», знак каждого слагаемого изменяем на противоположный. Затем приводим подобные слагаемые.
-45-3(9-y)=-45-27+3y=3y-72;
-6(8-b)+50=-48+6b+50=6b+2;
-35-5(х+8)=-35-5x-40=-5x-75;
2(3-а)-16=6-2a-16=-2a-10.

Спасибо огромное!Поняла все,хотя в алгебре ни в зуб ногой)))Спасибо за чудесный сайт.

Екатерина, на самом деле разобраться в алгебре не так уж и сложно. Успехов Вам!

a+(-3b)+(-c)+d
(-6x)+(-7y)+z
(-m)+(-4n)+(-3p)
(-0,6a)+(-b)+c+(-3d)
(-x)+6y+(-5z)
m+(-3n)+8p
Здравствуйте можете мне помочь?слегка затрудняюсь)я в 1-2 четверти пропустил эту тему о болезни и теперь не могу догнать а из за того что я неумею раскрывать скобки а не смогу делать другие темы)) пожалуйста помогите слегка

Если перед скобками стоит знак «+», при раскрытии скобок знаки слагаемых в скобках оставляем без изменений:
a+(-3b)+(-c)+d=a-3b-c+d
(-6x)+(-7y)+z=-6x-7y+z
(-m)+(-4n)+(-3p)=-m-4n-3p
(-0,6a)+(-b)+c+(-3d)=-0,6a-b+c-3d
(-x)+6y+(-5z)=-x+6y-5z
m+(-3n)+8p=m-3n+8p

Помогите еще раз)тут просто раскрыть скобки и привести подобные слагаемые:)
4(7-5х)-(12-20x)
2(3x-y)-(5x-2y)
6(x+2y)-3(2x+y)
5(4x+y)-2(x-y)
Спасибо заранее) ?

Алишер, если перед скобками стоит множитель, надо этот множитель умножить на каждое слагаемое, стоящее в скобках. При этом, если перед скобками стоит знак «+», знаки в скобках не изменяем. Если перед скобками стоит знак «-«, знак каждого слагаемого в скобках изменяем на противоположный. Затем приводим подобные слагаемые. Тема очень важная, постарайтесь разобраться с ней вовремя.
4(7-5х)-(12-20x)=28-20x-12+20x=16;
2(3x-y)-(5x-2y)=6x-2y-5x+2y=x;
6(x+2y)-3(2x+y)=6x+12y-6x-3y=9y;
5(4x+y)-2(x-y)=20x+5y-2x+2y=18x+7y.

Наверху приведены три основные правила расскрытия скобок: а) в случае, когда перед скобками стоит +; b) в случае, когда перед скобками стоит -; c) в случае, когда перед скобками стоит множитель

А каково правило, когда перед скобками стоит делитель?

Например:
270:(115-х) = 3
270:3=115-х
90=115-х
х=115-90
х=25
Вопрос: 115-х в скобках имеет знак плюс. Почему тогда при переносе в правую часть уравнения знак не меняется на противоположный?

Уважаемый Папа! Прекрасно помню, как писала Вам ответ, но обнаружила Ваш вопрос в списке ожидающих комментариев. Наверное, ответ не прошел (.
Если перед скобками стоит делитель, общего правила раскрытия скобок нет. Если требуется решить уравнение, как в данном случае, выражение в скобках рассматриваем как неизвестный делитель. Чтобы найти неизвестный делитель, делимое делим на частное. Знаки при этом не меняются. Знак меняется, если слагаемое переносим из одной части уравнения в другую.

Уважаемая Светлана Иванова! Просто удивляюсь Вашему терпению! Как Вы каждому отвечаете на однотипные комментарии!

На таких людях как Вы, самоотверженных и любящих свое дело, строится все доброе и светлое! Я вот студент, но давеча решил восстановить утерянную (никогда по сути не обретенную еще) школьную математику. Поэтому часто стал попадать на Ваш сайт по тем или иным запросам.

Искренно желаю Вам удачи в насаждении царицы наук в умы детей!

Помогите,
пожалуйста!
3(2y-1)+6(3y-4)=83+5(y-3)

Раскрываем скобки:6y-3+18y-24=83+5y-15. Упрощаем: 24y-27=5y+68. Переносим неизвестные — в одну строну, известные — в другую с противоположным знаком: 24y-5y=68+27, 19y=95. y=95:19, y=5.

А что, если стоит знак деления перед скобкой, а внутри скобки неврзможно выполнить действие? У нас вот такое уравнение: 38007:(4223-t)=9

В этом случае выражение в скобках рассматриваем как неизвестный делитель:4223-t=38007:9; 4223-t=4223. Теперь ищем неизвестное вычитаемое: t=4223-4223; t=0.

Здравствуйте подскажите как быть если + стоит после скобок вот такой пример
(2а— 56)2 + 10ab (2 в степени )

Если после скобок стоит «+», то он никак не влияет на действия в скобках.
(2a-5b)²+10ab=(2a)²-2∙2a∙5b+(5b)²+10ab=4a²-20ab+25b²+10ab=
=4a²-10ab+25b².

Сайт действительно не плохой, очень помогает, особенно после каникул, как известно после 3-х месяцев безделия, все забывается, а сейчас как раз то время, когда нужно вспомнить и даже что-то выучить. Молодцы ребята, стараются максимально, действительно не боюсь повториться, но сайт очень хороший, много полезного, спасибо, продолжайте в таком же духе.

Спасибо, Валерий! Успехов Вам в учёбе!

Добрый вечер. Объясните пожалуйста, как раскрыть скобки в примере 20(x-y)3= ?

Сергей, проще сначала перемножить числовые множители 20 и 3, а затем уже раскрывать скобки:20(x-y)3= 60(x-y)=60x-60y.

Здравствуйте,Светлана Иванова! Я чуть-чуть не поняла, как решать, если перед скобками стоит множитель . Выражение типа
−23⋅(−a−b+c). Как записать выражение без скобок? Спасибо.

Если перед скобками стоит множитель, этот множитель надо умножить на каждое слагаемое в скобках.
−23⋅(−a−b+c)=23a+23b+23c.

Если в скобках нет переменных т.е. вот так 2×(4+3), каков порядок действий?

Проще всего сначала выполнить действие в скобках, а результат умножить на множитель перед скобками: 2×(4+3)=2×7=14.

Здравствуйте, я не понял как решить такое уравнение 9(x+7)=-x

Уже разобрался,но как решить такое 7(х-1)=3х

Извините,все перечитал и разобрался,спасибо

Самые приятные комментарии — когда прочитали и разобрались самостоятельно. Ведь это не так уж и сложно, правда же?

Здравствуйте! А как разложить скобки в уравнении, если перед ними знак деления? 2/(m+1)=3m

Сергей, раскрывать скобки здесь не нужно. Здесь 2 — делимое, m+1 — делитель, 3m — частное. Отсюда 3m(m+1)=2.

Помогите, как раскрыть 9(t-1)(t+2)

9(t-1)(t+2)=9(t²+2t-t-2)=9t²+18t-9t-18=9t²+9t-18. Но это уже алгебра, а не математика 6 класса.

Сайт просто лучший! Все доходчиво и понятно! Авторам большое спасибо

А что если перед скобками делитель?

Вы имеете в виду знак деления? В общем случае правила нет. Записываем частное в виде дроби и пытаемся эту дробь сократить.

Пример 6:2(1+2). Как объяснить человеку, который пишет в ответе 9, что сначала надо раскрыть скобки? Есть правило? Такое, чтобы «дошло». Как я понимаю, ответ =1. Заранее благодарю!

Татьяна, существуют правила, определяющие порядок действий. Первым выполняются действия в скобках, затем — умножение и деление, затем — сложение и вычитание. В данном примере:

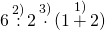
(знак умножения перед скобками обычно не пишут).
1)1+2=3;
2)6:2=3;
3)3∙3=9.
Ответ 1 получился бы в таком случае:
6:(2∙(1+2)).

Спасибо! Значит я была не права!

6:2(1+2) Попалось интересное суждение на эту тему. «Если считать, что знак умножения допустимо опускать в любом случае, то выражение очевидно преобразуется в 6/2*(2+1)=9.

Однако, так считают не все. Достаточно интуитивным является, что знак умножения допустимо опускать не во всех случаях, а только непосредственно между двумя сомножителями. Соответственно, ориентируясь на то, что знак умножения по факту опущен, считаем произведение 2(1+2) неразрывным и равным 6 и уже на него делим 6/6=1.

В качестве примера, где скрытое умножение обладает повышенным приоритетом по отношению к обычным умножению и делению можно считать «Курс теоретической физики» Ландау-Лифшица и другую физическую литературу. «»»» Ну там дальше есть формула, которую нет возможности здесь воспроизвести. В результате чего я подумала, что способ решения не один))). Но так как нам не задано в условии ничего, то решать надо просто, как вы и сказали. Что касается меня, то есть, как нас учили, то выражение 2(1+2) я вижу именно неразрывным.

помогите пожалуйста.Мне надо разложить на множители многочлен:
4с²-6х²с²+8с
заранее спасибо

Настя, это же не 6 класс. Вынесите общий множитель 2c за скобки. Получится 4с²-6х²с²+8с=2с(2с-3х²с+4).

Извините, добрый день.
Подскажите есть вот такой пример
(х-3)(х-4)(х-5)=(х-2)(х-4)(х-5)
и его решение
(х-3)(х-4)(х-5)-(х-2)(х-4)(х-5)=0
(x-4)(x-5)*(x-3-x+2)=0
-1(x-4)(x-5)=0
(x-4)(x-5)=0
x=4
x=5
Почему -1 умножили на (х-4) и всё равно осталось (х-4) ? куда делся минус ?

-1 не умножали на скобки. Обе части уравнения разделили на -1.

Здравствуйте! А если перед скобками вообще равно? Например х-2=(30-х)+2:2?

Энн, перед скобками стоит знак «+» (просто мы его не пишем). Соответственно, при раскрытии скобок знаки чисел, стоящих в скобках, оставляем без изменений.

Добрый день. Помогите, пожалуйста, решить уравнение 4,8:0,4=12:(0,4+3х)

Сначала можно упростить левую часть. 4,8:0,4=48:4=12.
12=12:(0,4+3х). Здесь 0,4+3х — делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное:0,4+3х=12:12.
0,4+3х=1. 3x — неизвестное слагаемое. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое: 3x = 1-0,4
3x = 0,6. Наконец, чтобы найти неизвестный множитель x, произведение делим на известный множитель:x = 0,6:3; x = 0,2.

Подскажите пожалуйста,как решить это уравнение-((x : 2 − 3) : 2 − 1) : 2 − 4 = 3

-((x : 2 − 3) : 2 − 1) : 2 = 3+4
-((x : 2 − 3) : 2 − 1) : 2 = 7
-((x : 2 − 3) : 2 − 1) = 7∙2
-((x : 2 − 3) : 2 − 1) = 14
(x : 2 − 3) : 2 − 1 = -14
(x : 2 − 3) : 2 = -14+1
(x : 2 − 3) : 2 = -13
x : 2 − 3 = -13∙2
x : 2 − 3 = -26
x : 2 = -26+3
x : 2 = -23
х= -23∙2
х= -46.

Здравствуйте Светлана! Зашел на Ваш сайт вспомнить раскрытие скобок,и вспомнил школьные годы. Как здорово, желаю Вам счастья и дооолгих лет жизни.

Спасибо Вам, Канатбай, на добром слове! И Вам тоже счастья и здоровья!

www.for6cl.uznateshe.ru