Закон распределения дискретной случайной величины. Примеры решения задач

Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные.

Дискретной случайной величиной называется случайная величина, принимающая лишь конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями.

Законом распределения дискретной случайной величины называется функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть задан одним из следующих способов.

1. Закон распределения может быть задан таблицей:

События X = x_i (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице: р₁+р₂+р₃+…+р_n = ∑p_i =1

2. Закон распределения может быть задан аналитически (формулой) P(X = x_i) = ϕ(x_i). Например:

а) с помощью биномиального распределения: P_n(X=k) = С_n k p k q n-k , 0 0, k = 0, 1, 2, … .

в) с помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X 2 или D(X) = M(X 2 )−[M(X)] 2 . Разность X–M(X) называют отклонением случайной величины от ее математического ожидания.
Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λ

• Среднее квадратическое отклонение (стандартное отклонение) σ(X)=√D(X).

Примеры решения задач по теме «Закон распределения дискретной случайной величины»

Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.

Решение. По условию задачи возможны следующие значения случайной величины X: 0, 10, 50, 100 и 500.

Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.

Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:

Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.

Решение. Случайная величина X числа очков принимает значения 1, 2, 3, 4, 5, 6. Вероятность того, что выпадет одно из данных значений равна 1/6. Закон распределения представим в виде таблицы:

Найдем математическое ожидание величины Х: М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5

Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины.

Решение. 1. Дискретная случайная величина X= имеет следующие возможные значения: х₁=0 (ни один из элементов устройства не отказал), х₂=1 (отказал один элемент), х₃=2 (отказало два элемента) и х₄=3 (отказали три элемента).

Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим вероятности значений:
P₃(0) = С₃ 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P₃(1) = С₃ 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P₃(2) = С₃ 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P₃(3) = С₃ 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p_i = 0,729+0,243+0,027+0,001=1.

Таким образом, искомый биномиальный закон распределения Х имеет вид:

www.ekonomika-st.ru

Случайные величины. Дискретная случайная величина.
Математическое ожидание

Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

Случайные величины, как правило, обозначают через 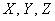*, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

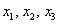* Иногда используют 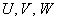, а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

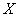– количество очков, которое выпадет после броска игрального кубика.

В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 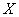может принять одно из следующий значений:

.

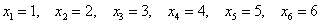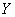– количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

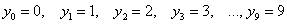, либо 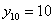мальчиков – один и только один из перечисленных вариантов.

И, дабы соблюсти форму, немного физкультуры:

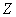– дальность прыжка в длину (в некоторых единицах).

Её не в состоянии предугадать даже мастер спорта 🙂

Тем не менее, ваши гипотезы?

Коль скоро, множество действительных чисел бесконечно, то случайная величина 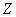может принять бесконечно много значений из некоторого промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

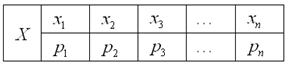
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

А теперь очень важный момент: поскольку случайная величина 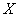обязательно примет одно из значений 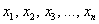, то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

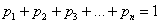
или, если записать свёрнуто:

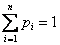
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

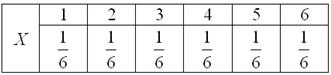
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

Некоторая игра имеет следующий закон распределения выигрыша:

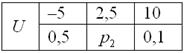
Найти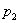

…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина 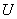может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

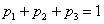
Разоблачаем «партизана»:

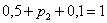
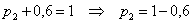– таким образом, вероятность выигрыша 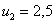условных единиц составляет 0,4.

Контроль: 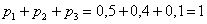, в чём и требовалось убедиться.

Ответ: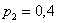

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 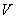– размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 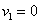рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
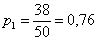– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

С остальными случаями всё просто. Вероятность выигрыша 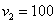рублей составляет:

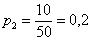
И для :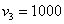

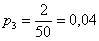
Проверка: 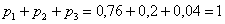– и это особенно приятный момент таких заданий!

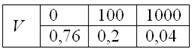
Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

Вероятность того, что стрелок поразит мишень, равна 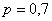. Составить закон распределения случайной величины 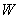– количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 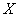принимает значения 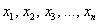с вероятностями 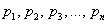соответственно. Тогда математическое ожидание 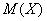данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

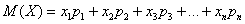
или в свёрнутом виде:

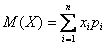
Вычислим, например, математическое ожидание случайной величины 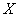– количества выпавших на игральном кубике очков:

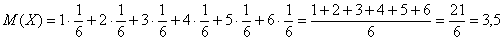очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

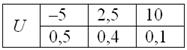
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

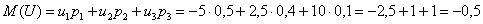, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 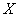– его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

Случайная величина 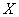задана своим законом распределения вероятностей:

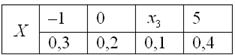
Найти 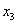, если известно, что 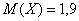. Выполнить проверку.

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

Решения и ответы:

Пример 3. Решение: по условию 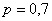– вероятность попадания в мишень. Тогда:
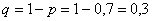– вероятность промаха.

Составим 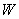– закон распределения попаданий при двух выстрелах:

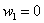– ни одного попадания. По теореме умножения вероятностей независимых событий:

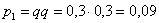
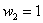– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

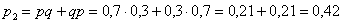
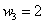– два попадания. По теореме умножения вероятностей независимых событий:

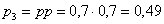
Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ: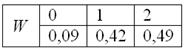

Примечание: можно было использовать обозначения 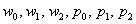– это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид:

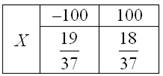
Вычислим математическое ожидание:

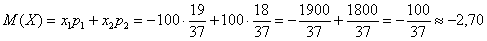
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания:

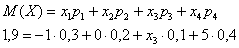
поменяем части местами и проведём упрощения:

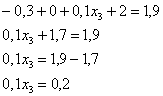
таким образом:

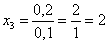
Выполним проверку:

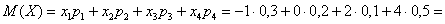
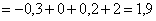, что и требовалось проверить.

Ответ: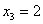

Автор: Емелин Александр

(Переход на главную страницу)

Качественные работы без плагиата – Zaochnik.com

mathprofi.ru

Основные законы распределения

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика.

Стоимость: 2000 руб / 90 мин.

Репетитор: Крюков Илья Хассанович

Предметы: математика, экономика, бухгалтерский учет.

Стоимость: 1600 руб / 60 мин.

Репетитор: Скрипаленко Михаил Михайлович

Предметы: математика (ЕГЭ), английский язык (GMAT, GRE (general), GRE subject test in maths, IELTS, TOEFL, BEC).

Стоимость: 1200 руб / 60 мин.

Репетитор: Матвеева Милада Андреевна

Предметы: русский язык, литература (ЕГЭ, ГИА).

Репетитор: Тверской Василий Борисович

Предметы: математика, физика.

Стоимость: 3500 руб / 90 мин.

Репетитор: Поздняков Андрей Александрович

Предметы: английский язык, (ЕГЭ). Подготовка к TOEFL и IELTS.

Стоимость: 2000 руб / 60 мин.

Репетитор: Ершикова Марина Львовна

Предметы: бухгалтерский учет (кроме банковского), налогообложение, аудит.

Стоимость: 1500 руб / 60 мин.

1.Биномиальный закон распределения.

Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.

Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.

В таблице m — число заказов, полученных компанией на покупку телевизора. С_n m — число сочетаний m телевизоров по n, p — вероятность наступления события А, т.е. заказа телевизора, q — вероятность не наступления события А, т.е. не заказа телевизора, P m,n — вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей.

2.Геометрическое распределение.

Геометрическое распределение случайной величины имеет следующий вид:

P m — вероятность наступления события А в испытание под номером m.
р — вероятность наступления события А в одном испытании.
q = 1 — p

Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.

Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 — что десятый блок оказался неисправным — 0,038742049 , 2 — что все проверяемые блоки оказались исправными — 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события P m (10 проверенных блоков) относительно высокая. Рис.2.

3.Гипергеометрическое распределение.

Гипергеометрическое распределение случайной величины имеет следующий вид:

Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M — всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m — число правильно угаданных чисел среди изъятых.

Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.

4.Закон распределения Пуассона.

Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:

λ = np = const
n — число испытаний, стремящиеся к бесконечности
p — вероятность наступления события, стремящаяся к нулю
m — число появлений события А

Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B — 0,06 и C — 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.

Из условия имеем: m=100, λ 1 =8, λ 2 =6, λ 3 =4 ( ≤10 )

(таблица дана не полностью)

Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)

Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.

5.Равномерный закон распределения.

Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.

6.Нормальный закон распределения (закон Гаусса).

Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:

где
а — математическое ожидание случайной величины
σ — среднее квадратическое отклонение

График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:

При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.

Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:

Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть — от а до х. (Рис.7)

www.mathtask.ru