Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!

Физика — рефераты, конспекты, шпаргалки, лекции, семинары

Закон изменения импульса. Закон сохранения импульса

В производную dP/dt войдут слагаемые midvi /dt. По закону Ньютона каждое такое слагаемое можно приравнять результирующей внешней силе Fi и результирующей внутренней силе fi со стороны остальных частиц.

При суммировании Fi и fi сумма всех внутренних сил будет равна нулю, так как, например, для силы f12 согласно третьему закону Ньютона найдётся равная по модулю и противоположная сила f21. Импульс системы можно представить как произведение общей массы m системы на некоторую скорость VC, которую называют скоростью центра масс системы. Формулировка закона изменения импульса в терминах центра масс От закона изменения импульса легко перейти к закону сохранения импульса:
Fi = 0, F = 0, P = const.

Механическая система, на которую не действуют никакие внешние силы, называется замкнутой системой.
В замкнутой механической системе импульс есть величина постоянная.
В терминах центра масс этот закон формулируется так:
Fi = 0, F = 0, VC = const;

Центр масс замкнутой механической системы покоится или движется равномерно и прямолинейно.

Закон сохранения и изменения энергии.

Рассмотрим сначала простейшую систему, состоящую из одного точечного тела.
Далее уравнение скалярно помножим на перемещение dl = vdt. В результате слева будет величина m(v) = d(0,5v2) = dEk, Величина Ek = 0,5mv2 была названа кинетической энергией. Справа появится величина
(F) = Fldl = ?A. Эту величину называют элементарной работой силы на отрезке пути dl.
На каком-либо участке траектории работа действующих на тело всех сил равна изменению кинетической энергии тела.

В случае силового поля внешних неподвижных тел работа по перемещению какого-либо пробного тела не зависит от формы пути, а зависит лишь от начального и конечного положений тела. Это позволяет ввести потенциальную энергию тела (наряду с кинетической). Представим себе, например, лёгкое заряженное тело имеет на бесконечном удалении от одноимённо заряженного внешнего массивного тела скорость v и начинает приближаться. По мере приближения пробное тело замедляется и в какой-то момент останавливается. Кинетическая энергия в этот момент равна нулю.

Но какой смысл говорить, что движение исчезло, если в следующие моменты тело вновь приобретёт скорость? Резонней говорить о переходе открытой (явной ) формы движения (кинетическая энергия) в некую скрытую форму. Какой же мерой обладает тело в точке остановки по сравнению с кинетической энергией на бесконечном удалении? Такой мерой является возможность совершения работы над телом при перемещении из данного положения в бесконечность (где тело уже не испытывает влияния силового центра).

Потенциальной энергией тела в силовом постоянном поле называют запас возможной работы при перемещении тела из данного положения в некоторое нулевое (стандартное) положение. Работу по перемещению тела из положения 1 в положение 2 можно выразить через изменение потенциальной энергии. Сила есть взятый со знаком «-» градиент потенциальной энергии.
Введение потенциальной энергии позволяет сформулировать закон сохранения энергии для материальной точки. В консервативных системах полная механическая энергия, равная сумме кинетической и потенциальной энергий, сохраняется.

Эта формулировка подходит и для системы из N материальных точек. В этом случае потенциальная энергия может быть подразделена на потенциальную энергию в поле внешних консервативных сил и потенциальную энергию взаимодействия частиц между собой. Аналогично, кинетическая энергия системы может быть представлена как сумма кинетической энергии движения системы как целого (половина произведения массы всей системы на квадрат скорости центра масс) и кинетической энергии движения частиц относительно центра масс. В случае, если внешнее силовое поле является однородным (как, например, поле силы тяжести), то потенциальную энергию можно записать как энергию тела с массой всей системы и с координатами центра масс.

Закон изменения механической энергии формулируется для случая, когда создающие силовое поле внешние тела движутся в выбранной системе отсчёта. Соответствующее этому силовое поле изменяется со временем. Силы называют сторонними, или неконсервативными. Изменение полной энергии равно работе сторонних (неконсервативных) сил. К сторонним силам можно отнести и диссипативные силы, действующие внутри системы.

worldofscience.ru

Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Закон изменения и закон сохранения импульса материальной точки

Закон сохранения импульса материальной точки. Этот закон следует из теоремы об изменении импульса и читается так если равнодействующая сил, приложенных к материальной точке, равна нулю, вектор импульса тела остается величиной постоянной во все время движения, т. е. [c.111]

Мы пришли к закону сохранения импульса системы импульс замкнутой системы материальных точек есть величина постоянная, или, другими словами, в отсутствие внешних сил сумма импульсов всех точек системы остается постоянной, какие бы изменения внутри системы ни происходили. Это значит, что в процессе взаимодействия частицы системы лишь обмениваются импульсами, оставляя полный импульс системы неизменным. [c.116]

Методическое замечание к понятию импульса. Закон сохранения импульса изолированной материальной точки и форма основного уравнения динамики (9.1) дают возможность логически просто и последовательно ввести понятие силы и второй закон Ньютона, Если импульс тела изучить до законов Ньютона, то закон инерции можно сформулировать как закон сохранения импульса изолированной материальной точки. Далее следует постулировать сохранение импульса в замкнутой системе материальных точек. Взаимодействие в такой системе будет заключаться в передаче импульса от одних точек к другим, а сила, действующая на материальную точку, будет некоторой функцией положения рассматриваемой точки относительно остальных, определяющей скорость передачи импульса рассматриваемой точки от других точек системы. Уравнение (9.1), т. е. второй закон Ньютона, запишется как следствие закона сохранения импульса системы точек импульс, полученный материальной точкой (в единицу времени), равен импульсу, переданному ей другими точками. Анализ процесса обмена импульсом между двумя точками немедленно приводит к следствию — третьему закону Ньютона. Важно, что трактовка силы н второго закона Ньютона в форме (9.1) без каких-либо изменений применима к действию на материальную точку физического поля. В этой трактовке сила есть скорость передачи импульса точке полем, определяющаяся параметрами поля и положением точки в нем. Это значит, что понятие силы находит обобщение за пределами чисто механической концепции взаимодействия (см. 5). Также объясняется ограниченность применения третьего закона Ньютона при наличии полей обмен импульсами может происходить между телом и полем, между телами через поле, но не непосредственно между двумя телами. [c.112]

Теорема об изменении импульса системы. Закон сохранения импульса. Теоремы для системы материальных точек удобно получать, обобщая рассмотренные ранее соответствующие теоремы для одной материальной точки. Теорему об изменении импульса материальной точки в форме (9.1) напишем для каждой /-й точки системы, подразделяя силы на внутренние и внешние [c.135]

Прямая задача динамики для системы материальных точек сводится к решению системы ЗN дифференциальных уравнений, так как уравнение движения вида (11.1) для каждой из N точек системы дает в проекции на координатные оси три дифференциальных уравнения для координат точки хД/),>>Д ), ,(/). Строгое аналитическое решение удается найти лишь в исключительных случаях, поэтому обычно используют приближенные методы. Однако существует несколько строгих общих законов, которые хотя сами по себе и не позволяют в общем случае найти траектории отдельных точек системы, вместе с тем дают важную информацию о движении системы в целом. Это закон (или теорема) о движении центра масс и три закона изменения и сохранения импульса, момента импульса и механической энергии системы материальных точек. Их выводу и обсуждению посвящена настоящая глава. [c.38]

Как известно из классической механики, систему из N частиц в случае пренебрежения их пространственной структурой (т. е. когда частицы рассматриваются как материальные точки) можно описать при помощи ЗМ дифференциальных уравнений, которым соответствуют 6Л интегралов движения, т. е. величин, сохраняющихся при изменениях, происходящих в системе. Полное число интегралов движения, естественно, задается тем, что в каждый момент времени система определяется ЗМ координатами и ЗА импульсами частиц (см., например, [1]). Среди 6А интегралов движения ) не все играют одинаковую роль. Чтобы выяснить эту роль, рассмотрим изолированную систему, т. е. систему, которая не подвержена действию внешних сил ). Для такой системы имеется десять интегралов движения, которые соответствуют физическим величинам, всегда сохраняющимся при любом произвольном взаимодействии между частицами системы во время движения. Эти величины, по крайней мере, в принципе можно измерить на опыте в рамках классической механики. 10 интегралов движения можно представить, в соответствии с их физическим смыслом, следующим образом 10 = 4-1-3-2. Цифра 4 соответствует закону сохранения [c.9]

Теорема об изменении момента импульса системы. Закон сохранения момента импульса. Теорему об изменении момента импульса для одной материальной точки мы получили в 10 и кратко выразили уравнением (10.4). В правой части уравнения стоит сумма моментов сил, или момент равнодействующей силы, приложенной к материальной точке. [c.136]

Сформулируйте второй закон Ньютона для системы материальных точек напишите его в виде формулы. Поясните, почему в изменении импульса системы играют роль только внешние силы. Скажется ли на движении центра масс отсутствие в системе внутренних сил Запишите закои сохранения импульса в виде трех скалярных уравнений и сформулируйте следствия из них. Сформулируйте этот закон через ускорение центра масс. Может ли центр масс системы находиться в таком месте, где нет никакой материальной точки Можно ли сумму внешних сил, действующих на систему, называть равнодействующей [c.121]

В первой главе было показано, что задача о движении одной точки имеет обнхее решение для сравнительно широкого класса сил. Задача о движении двух точек также имеет общее решение в квадратурах при достаточно общих предположениях о силе взаимодействия между точками (см. 3.1). Однако отыскание общего решения задачи трех и более точек при достаточно общих предположениях о силах взаимодействия встречает непреодолимые трудности. В связи с этим общие теоремы, справедливые при любом числе материальных точек, приобретают громадное значение. Такими универсальными теоремами являются законы изменения и сохранения импульса, кинетического момента и энергии. Рассмотрим ЭТ1И законы для механических систем свободных точек (см. с. 26), или, кратко говоря, для свободных систем. [c.60]

Смотреть страницы где упоминается термин Закон изменения и закон сохранения импульса материальной точки : [c.86] [c.251] [c.71] Смотреть главы в:

mash-xxl.info

Закон изменения и сохранения полной механической энергии

11)Закон изменения и сохранения полной механической энергии

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

Какие причины могут изменить полную механическую энергию?

Рассмотрим систему тел, в которой действуют следующие силы:

Изменение кинетической энергии системы равно суммарной работе всех сил, действующих на тела этой системы (см. тему 3):

Изменение потенциальной энергии системы равно работе потенциальных сил с обратным знаком (см. тему 4):

Очевидно, что изменение полной механической энергии равно:

Из уравнений (1-3) получим, что изменение полной механической энергии равно суммарной работе всех внешних сил и внутренних непотенциальных сил.
DE_к = A_внеш.с.+ A_{непот.с.} (4)

Формула (4) представляет из себя закон изменения полной механической энергии системы тел.

Существует 2 причины изменения энергии системы:

Очевидно, что полная механическая энергия замкнутой системы, в которой действуют только потенциальные силы, не изменяется при любых перемещениях тел. Это утверждение называется законом сохранения механической энергии.

12) ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА

система отсчёта, в к-рой справедлив закон инерции: матер. точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения. Всякая система отсчёта, движущаяся по отношению к И. с. о. поступательно, равномерно и прямолинейно, есть также И. с. о. Следовательно, теоретически может существовать любое число равноправных И. с. о., обладающих тем важным св-вом, что во всех таких системах законы физики одинаковы (принцип относительности). В любой И. с. о. справедливы также второй закон Ньютона и законы сохранения кол-ва движения (импульса), момента кол-ва движения и движения центра инерции (центра масс) для замкнутых, не подверженных внеш. воздействиям систем. Система отсчёта, движущаяся по отношению к И. с. о. с ускорением, явл. неинерциальной, и ни закон инерции, ни др. названные законы в ней не выполняются.

Понятие «И. с. о.» явл. научной абстракцией. Реальная система отсчёта всегда связывается с к.-н. конкретным телом (Землёй, корпусом корабля или самолёта и т. п.), по отношению к к-рому и изучается движение тех или иных объектов. Поскольку в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звёздам), то любая реальная система отсчёта может рассматриваться как И. с. о. лишь с той или иной степенью приближении. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звёздную) систему с началом в центре масс Солн. системы и с осями, направленными на три звезды. Такая И. с. о. используется гл. обр. в задачах небесной механики и космонавтики. Для решения большинства технич. задач И. с. о. можно считать систему, жёстко связанную с Землёй, а в случаях, требующих большей точности (напр., в гироскопии),— с началом в центре Земли и осями, направленными на звёзды.

При переходе от одной И. с. о. к другой в классич. механике Ньютона для пространств. координат и времени справедливы преобразования Галилея (см. ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ), а в релятив. механике — Лоренца преобразования.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА

— система отсчёта, в к-рой справедлив закон инерции: материальная точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения. Всякая система отсчёта, движущаяся по отношению к И. с. о. поступательно, равномерно и прямолинейно, есть также И. с. о. Следовательно, теоретически может существовать любое число равноправных И. с. о., обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (принцип относительности). Система отсчёта, движущаяся по отношению к И. с. о. с ускорением, неинерциальна, и закон инерции в ней не выполняется. 2 . Опыт Майкельсона–Морли, неоднократно повторенный впоследствии со все более возрастающей точностью, дал отрицательный результат. Анализ результатов опыта Майкельсона–Морли и ряда других экспериментов позволил сделать вывод о том, что представления об эфире как среде, в которой распространяются световые волны, ошибочно. Следовательно, для света не существует избранной (абсолютной) системы отсчета. Движение Земли по орбите не влияет на оптические явления на Земле.

Исключительную роль в развитии представлений о пространстве и времени сыграла теория Максвелла. К началу XX века эта теория стала общепризнанной. Предсказанные теорией Максвелла электромагнитные волны, распространяющиеся с конечной скоростью, уже нашли практическое применение – в 1895 году А. С. Поповым было изобретено радио. Но из теории Максвелла следует, что скорость распространения электромагнитных волн в любой инерциальной системе отсчета имеет одно и то же значение, равное скорости света в вакууме. Это значит, что уравнения, описывающие распространение электромагнитных волн, не инвариантны относительно преобразований Галилея. Если электромагнитная волна (в частности, свет) распространяется в системе отсчета K’ (рис. 4.1.1) в положительном направлении оси x’, то в системе K свет должен, согласно галилеевской кинематике распространяться со скоростью c + υ, а не c.

Итак, на рубеже XIX и XX веков физика переживала глубокий кризис. Выход был найден Эйнштейном ценой отказа от классических представлений о пространстве и времени. Наиболее важным шагом на этом пути явился пересмотр используемого в классической физике понятия абсолютного времени. Классические представления, кажущиеся наглядными и очевидными, в действительности оказались несостоятельными. Многие понятия и величины, которые в нерелятивистской физике считались абсолютными, т. е. не зависящими от системы отсчета, в эйнштейновской теории относительности переведены в разряд относительных.

Так как все физические явления происходят в пространстве и во времени, новая концепция пространственно-временных закономерностей не могла не затронуть в итоге всю физику.

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

1. Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

2. Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Эти принципы следует рассматривать как обобщение всей совокупности опытных фактов. Следствия из теории, созданной на основе этих принципов, подтверждались бесконечными опытными проверками. СТО позволила разрешить все проблемы «доэйнштейновской» физики и объяснить «противоречивые» результаты известных к тому времени экспериментов в области электродинамики и оптики. В последующее время СТО была подкреплена экспериментальными данными, полученными при изучении движения быстрых частиц в ускорителях, атомных процессов, ядерных реакций и т. п.

Постулаты СТО находятся в явном противоречии с классическими представлениями. Рассмотрим такой мысленный эксперимент: в момент времени t = 0, когда координатные оси двух инерциальных систем K и K’ совпадают, в общем начале координат произошла кратковременная вспышка света. За время t системы сместятся относительно друг друга на расстояние υt, а сферический волновой фронт в каждой системе будет иметь радиус ct (рис. 4.1.3), так как системы равноправны и в каждой из них скорость света равна c.

С точки зрения наблюдателя в системе K центр сферы находится в точке O, а с точки зрения наблюдателя в системе K’ он будет находиться в точке O’. Следовательно, центр сферического фронта одновременно находится в двух разных точках!

Причина возникающего недоразумения лежит не в противоречии между двумя принципами СТО, а в допущении, что положение фронтов сферических волн для обеих систем относится к одному и тому же моменту времени. Это допущение заключено в формулах преобразования Галилея, согласно которым время в обеих системах течет одинаково:t = t’. Следовательно, постулаты Эйнштейна находятся в противоречии не друг с другом, а с формулами преобразования Галилея. Поэтому на смену галилеевых преобразований СТО предложила другие формулы преобразования при переходе из одной инерциальной системы в другую – так называемые преобразования Лоренца, которые при скоростях движения, близких к скорости света, позволяют объяснить все релятивисткие эффекты, а при малых скоростях (υ

studopedia.org — Студопедия.Орг — 2014-2018 год. (0.003 с) .

studopedia.org

Закон сохранения и изменения

Закон изменения момента импульса.

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей L_i , взятых относительно одной и той же точки выбранной системы отсчета.

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы .

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

.

Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.

В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.

Закон сохранения момента импульса.

Из закона изменения момента импульса, полученного нами для системы тел, вытекает закон сохранения момента импульса применительно к механике:

момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Еще раз подчеркнем, что при использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.

Закон сохранения момента импульса является фундаментальным законом природы и выполняется для любых, а не только механических систем.

Следствия из закон сохранения момента импульса :

· в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;

· если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;

· в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Примеры :
к первому следствию — при движении человека, находящегося на поверхности диска, по окружности с центром, совпадающим с центром масс диска, последний начинает

поворачиваться в сторону, противоположную движению человека относительно Земли;
ко второму следствию — ко второму следствию — студент, держащий в вытянутых расправленных руках гантели, сидит на скамье (скамье Жуковского), которая вращается вокруг вертикальной оси. В случае приближения гантелей к груди угловая скорость движения системы “ скамья-студент-гантели ” увеличивается.

к третьему следствию к третьему следствию — в начальный момент времени студент сидит на неподвижной скамье Жуковского и удерживает в руках раскрученное колесо. Пусть ось вращения колеса перпендикулярна оси вращения Z скамьи Жуковского, т. е. расположена в горизонтальной плоскости. При повороте колеса на 90 о в вертикальной плоскости проекция момента импульса системы “скамья-студент-колесо” на вертикальную ось L_z не изменится и останется равной нулю.

Следовательно, вектора угловых скоростей системы “студент-скамья” и колеса направлены в противоположные стороны.

Сохранение момента импульса и изотропность пространства.

Изотропность пространства обусловлена симметрией пространства к операции поворота . В случае поворота замкнутой системы на угол a относительно выбранной ИСО работу могут совершить только внутренние силы. При этом работа консервативных сил, зависящая исключительно от изменения взаимного расположения частей системы, равняется нулю. Неконсервативные силы ввиду отсутствия относительного движения частей системы работы не совершают. Следовательно, работа всех внутренних сил системы равняется нулю.

Из уравнения вытекает, что результирующий момент внутренних сил в замкнутой системе отсчета также равен нулю

В соответствии с законом динамики вращательного движения и уравнением момент импульса замкнутой системы при осуществлении операции ее поворота сохраняется.

Таким образом, соблюдение условия позволяет получить закон сохранения момента импульса замкнутой системы, используя для этого вместо третьего закона Ньютона одно из свойств симметрии пространства — его изотропность .

www.kvadromir.narod.ru

Закон изменения и сохранения момента импульса

ДИНАМИКА ТВЕРДОГО ТЕЛА

ЛЕКЦИЯ 5

Твердое тело можно рассматривать как систему материальных точек, жестко связанных друг с другом. Оказывается, что количество уравнений для описания отдельных видов движений можно значительно уменьшить, если ввести физические величины, которые относятся ко всему твердому телу.

Рассмотрим произвольную систему частиц (материальных точек), которая перемещается относительно некоторой неподвижной точки О (рис. 4.1). Для каждой точки данной системы запишем второй закон Ньютона

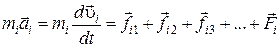, (5.1)

где 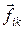(k = 1, 2, …, n) представляют собой внутренние силы взаимодействия всех элементов тела с выбранным элементом i, а – равнодействующая всех внешних сил, действующих на этот элемент, m_i – масса i-го элемента.

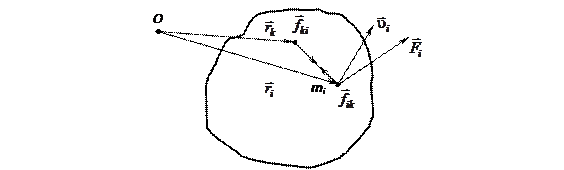
Умножим векторно слева уравнение (5.13) на радиус — вектор точки i-го элемента, :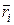

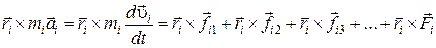. (5.2)

Преобразуем левую часть:

(5.3)

Величина 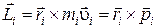в (5.3) называется моментом импульса материальной точки (векторное произведение радиус – вектора точки на ее импульс).

Величину, равную векторному произведению радиус-вектора точки на вектор силы, действующей на точку A, на­зывают моментом силы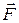относительно точки О(рис. 4.5). Таким образом, величина в правой части (5.15) есть момент внешней силы, действующей на точку i. Величина в уравнении (5.2), равная:

,

есть сумма моментов всех внутренних сил, действующих на точку i. С учетом введенных обозначений уравнение (5.2) примет вид:α

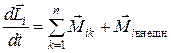. (5.4)

Просуммируем уравнения движения по всем n элементам системы:

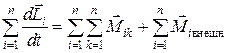. (5.5)

Левая часть (5.5) представляет собой момент импульса системы, который равен векторной сумме моментов составляющих систему точек:

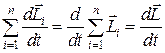. (5.6)

Первое слагаемое в (5.5) есть сумма моментов всех внутренних сил, действующих на систему. Можно показать, что эта сумма равна нулю. В самом деле, рассмотрим сумму моментов внутренних сил для двух точек, i и k (рис. 5.1). Учитывая, что по 3-му закону динамики 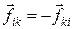, получим:

,

так как вектор, равный разности 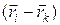, направлен вдоль сил 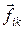и . Если попарно просуммировать моменты внутренних сил, то получим, что сумма моментов всех внутренних равна нулю.

Уравнение (5.5) для тела из 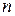материальных точек можно представить в виде:

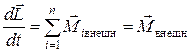. (5.7)

Таким образом, скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. Согласно урав­нению (5.7) момент импульса системы может изменять­ся под действием только суммарного момента всех внеш­них сил.

Если внешние силы отсутствуют, т.е. 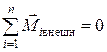, то система замкнута и из (4.7) следует закон сохранения момента им­пульса механической системы: момент импульса замкнутой системы частиц остается по­стоянным.

Моменты импульса отдельных частей или час­тиц замкнутой системы могут изменяться со временем, однако эти изменения всегда происходят так, что приращение мо­мента импульса одной части системы равно убыли мо­мента импульса ее другой части (относительно одной и той же точки системы отсчета).

Момент импульса 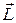сохраняется для незамкнутых систем, у ко­торых, импульс 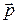меняется со временем. Если относительно некоторой точки О выбранной систе­мы отсчета суммарный момент внешних сил , то, со­гласно (5.7), момент импульса системы относительно точки О сохраняется.

В частном случае у незамкнутых систем может сохраняться не сам момент импульса 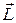, а его проекция на некоторую неподвижную ось z, когда проекция суммарного момента всех внешних сил на эту ось равна нулю. За­писав уравнение (5.7) в проекциях на ось z, получим:

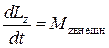. (5.8)

Здесь L_iz и М_{iz внешн} — момент импульса и суммарный мо­мент внешних сил относительно оси z для i-й частицы системы:

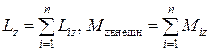. (5.9)

Из уравнения (5.8) следует, что если проекция М_zвнешн =0, то момент импульса системы относи­тельно этой оси сохраняется:

.

Момент силы относительно оси z в (5.8) можно определить, раскрыв векторное произведение по формуле:

где величина l =rsinα называется плечом силы (кратчайшее расстояние от оси до направления действия силы, см. рис.5.2).

Пример 5-1. Расчет момента сил трения.

Диск, радиус которого R и масса m вращается на плоской поверхности вокруг неподвижной оси (рис.4.3). Коэффициент трения скольжения материала диска равен m. Найти момент сил трения диска о поверхность

Момент сил трения, действующих на весь диск, алгебраически складывается из моментов сил трения, действующих на элементарные участки диска массой dm, и направлен перпендикулярно его плоскости (рис.5.3).

Выделим элемент объема dV = drdrda диска на расстоянии r от центра (d – толщина диска). Сила трения скольжения, приложенная к этому элементу равна dF = mgdm. Момент силы трения скольжения для элемента, находящегося на расстоянии r от оси вращения равен:

где dm = rdV = rdrdrda – масса элемента объема диска. Тогда суммарный момент сил трения получим, интегрируя выражение для dM по r в пределах от 0 до R и по a в пределах от 0 до 2π:

.

При получении последнего выражения учитывалось, что масса диска равна m = rdpR 2 .

. Наряду с за­конами сохранения энергии и импульса закон сохранения момента импульса является одним из фундаментальных законов природы.

studopedia.ru