Теория электрической связи: курс лекций

1. Информация и информационные системы
1.1. Основные понятия и определения
1.2. Контрольные вопросы

2. Математические модели детерминированных сигналов
2.1. Принципы Фурье-анализа сигналов
2.2. Разложение в ряд Фурье
2.3. Интеграл Фурье
2.4. Свойства преобразования Фурье
2.4.1. Сдвиг во времени
2.4.2. Сдвиг по частоте
2.5. Полезные функции
2.5.1. Дельта-функция
2.5.2. Спектр синусоидального и косинусоидального сигналов
2.5.3. Спектр последовательности прямоугольных импульсов
2.6. Энергетическое толкование спектра сигнала
2.7. Практическая ширина спектра сигнала
2.8. Применение методов Фурье к анализу линейных систем
2.8.1. Свертка
2.8.2. Графическая иллюстрация свертки
2.8.3. Свертка по времени
2.8.4. Свертка по частоте
Контрольные вопросы

3. Математические модели случайных сигналов
3.1. Случайные сигналы и их вероятностные характеристики
3.2. Числовые характеристики случайного процесса
3.3. Стационарные случайные процессы
3.4. Свойства корреляционной функции стационарного случайного процесса
3.5. Эргодичность стационарных процессов
3.6. Спектральная плотность случайного процесса
3.7. Широкополосные и узкополосные процессы
3.8. Эффективная ширина спектра случайного процесса
Контрольные вопросы

4. Модуляция сигналов
4.1. Основные понятия
4.2. Амплитудная модуляция
4.3. Угловая модуляция
4.4. Импульсная модуляция
4.5. Векторное представление сигналов
4.6. Детектирование высокочастотных колебаний
4.7. Цифровая модуляция
4.7.1. Амплитудная манипуляция, ASK
4.7.2. Фазовая манипуляция, PSK
4.7.3. Частотная манипуляция, FSK
4.7.4. Амплитудно-фазовая манипуляция, АРК
Контрольные вопросы

5. Квантование сигналов
5.1. Способы квантования сигналов
5.2. Дискретизация по времени
5.3. Равномерная дискретизация
5.3.1. Частотный критерий Котельникова–Найквиста (теорема отсчетов)
5.3.2. Корреляционный критерий Железнова
5.3.3. Критерий допустимого отклонения
5.4. Равномерное квантование
5.5. Неравномерное квантование
Контрольные вопросы

6. Кодирование источника. Основы теории информации
6.1. Дискретные источники информации
6.1.1. Количество информации и энтропия
6.1.2. Передача информации по каналу связи
6.2. Оптимальное кодирование двоичного источника
6.3. Алгоритмы кодирования дискретных источников
6.3.1. Алгоритм кодирования Хаффмена
6.3.2. Алгоритм кодирования Шеннона–Фано
6.3.3. Алгоритм Лемпела–Зива
6.4. Кодирование непрерывных источников
6.4.1. Энтропия непрерывной случайной величины и её свойства
6.4.2. Пропускная способность непрерывного канала связи
6.4.3. Обмен мощности сигнала на ширину его спектра
6.4.4. Эпсилон-энтропия источника непрерывных сообщений
Контрольные вопросы

7. Анализ эффективности телекоммуникационных систем
7.1. Показатели эффективности телекоммуникационных систем
7.2. Эффективность систем передачи дискретных сообщений
7.3. Эффективность аналоговых систем передачи
7.4. Способы повышения эффективности телекоммуникационных систем
7.4.1. Перераспределение плотностей вероятностей элементов сообщения
7.4.2. Декорреляция сообщений
7.4.3. Оптимальное статистическое кодирование
Контрольные вопросы

8. Канальное кодирование
8.1. Основные понятия и определения
8.2. Линейные блочные коды
8.2.1. Кодирование сообщений. Производящая матрица
8.2.2. Пример генерации кода (6,3)
8.2.3. Декодирование сообщений. Проверочная матрица
8.2.4. Общие принципы помехоустойчивого кодирования
8.2.5. Декодирование с исправлением ошибок
8.2.6. Пример декодирования с исправлением ошибок для кода (6,3)
8.2.7. Совершенные и квазисовершенные коды. Код Хэмминга
8.2.8. Оценка возможностей кода
8.3. Циклические коды
8.3.1. Общие свойства циклических кодов
8.3.2. Кодирование сообщений
8.3.3. Декодирование сообщений
8.4. Рекуррентные коды
8.5. Сверточные коды
8.5.1. Кодирование сообщений
8.5.2. Декодирование сообщений. Мягкое и жесткое декодирование
Контрольные вопросы

9. Теория помехоустойчивости систем связи
9.1. Задачи оптимального приема информации
9.2. Фильтрация сигналов
9.2.1. Частотная фильтрация
9.2.2. Метод накопления
9.2.3. Корреляционная фильтрация
9.2.4. Согласованная фильтрация
9.3. Оптимальный прием сигналов при наличии помех
9.4. Обнаружение сигналов
9.4.1. Оптимальное обнаружение полностью известного сигнала (когерентный прием)
9.4.2. Корреляционный когерентный прием
9.4.3. Согласованная фильтрация при когерентном приеме
9.4.4. Примеры синтеза согласованных фильтров
9.4.5. Оптимальное обнаружение сигнала со случайной начальной фазой (некогерентный прием)
9.4.6. Корреляционный некогерентный прием
9.4.7. Согласованная фильтрация при некогерентном приеме
9.4.8. Оптимальное обнаружение сигналов со случайной амплитудой и начальной фазой
9.5. Различение сигналов
9.5.1. Когерентное различение сигналов
9.5.2. Некогерентное различение сигналов
9.5.3. Различение сигналов в условиях многолучевости
9.6. Прием оптических сигналов
Контрольные вопросы

10. Многоканальные системы связи
10.1. Линейное уплотнение и разделение каналов
10.1.1. Системы с временным разделением каналов (ВРК)
10.1.2. Системы с частотным разделением каналов (ЧРК)
10.1.3. Системы с кодовым разделением каналов (КРК)
10.1.4. Системы с поляризационным и пространственным разделением каналов
10.2. Нелинейное уплотнение и разделение каналов
10.2.1. Комбинационное разделение каналов (КРК)
10.2.2. Мажоритарное разделение каналов (МРК)
10.3. Взаимные помехи между каналами
10.3.1. Переходные затухания на ближнем и дальнем конце
10.3.2. Пропускная способность многоканальных систем
10.4. Способы увеличения дальности связи
Контрольные вопросы

www.techbook.ru

Корольов / Теория связи

УДК 621.391 (075) ББК 32.8 я 7

Утверждено редакционно-издательским советом университета в качестве учебного пособия

Доктор технических наук, профессор Кумунжиев К.В.

Кафедра радиоэлектроники Ульяновского высшего военного инженерного училища связи

Авторы: К.К. Васильев, В.А. Глушков, А.В. Дормидонтов, А.Г. Нестеренко

Теория электрической связи: учебное пособие / К.К. Васильев, В.А. Глуш- Т 33 ков, А.В. Дормидонтов, А.Г. Нестеренко; под общ. ред. К.К. Васильева. —

Ульяновск: УлГТУ, 2008. — 452 с. ISBN 978-5-9795-0203-8

Излагаются основные закономерности и методы анализа потенциальной помехоустойчивости и пропускной способности каналов связи. Рассматриваются параметры и характеристики сообщений, сигналов и помех, их математические модели, методы формирования и преобразования сигналов, вопросы теории передачи и кодирования сообщений, алгоритмы цифровой обработки сигналов, основные модели каналов электросвязи, принципы многоканальной связи и распределения информации, вопросы оценки эффективности систем связи и теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах.

Книга предназначена студентам, обучающимся по направлению 654400 — Телекоммуникации.

© Васильев К. К., Глушков В. А., Дормидонтов А. В., Нестеренко А. Г., 2008

ISBN 978-5-9795-0203-8 © Оформление. УлГТУ, 2008

Пособие написано на основе опыта чтения авторами лекций по теории электрической связи. Базируясь на ранее опубликованных изданиях [8, 9, 12, 13, 14, 15], авторы обобщили и собрали воедино материалы [1, 17, 20, 22, 34], опубликованные в последние годы, дополнив их новыми информационными технологиями. Основными особенностями настоящего пособия является рассмотрение вопросов корреляционного анализа; эталонной модели взаимодействия открытых систем как единой идеологии проектирования систем связи; комплексного представления сигналов; некоторых методов модуляции, таких как квадратурная относительно-фазовая манипуляция и частотная модуляция с непрерывной фазой; методы сжатия дискретных сообщений; более детальное рассмотрение некоторых методов помехоустойчивого кодирования (коды БЧХ, Рида-Соломона, Рида-Маллера); уделено особое внимание методам приема сигналов в сложных условиях и теоретико-информационным основам криптозащиты сообщений в телекоммуникационных системах.

Настоящее учебное пособие состоит из десяти глав, в которых последовательно рассматриваются основополагающие вопросы теории электрической связи. Остановимся более подробно на содержании глав.

В первой главе пособия рассматриваются сообщения, сигналы и помехи, их математические модели, временное и спектральное представление сигналов и помех.

Во второй главе представлены методы формирования и преобразования дискретных сигналов, временные и спектральные характеристики манипулированных сигналов.

В третьей главе пособия анализируются оптимальные методы приема при различных видах передачи и способы реализации потенциальной помехоустойчивости.

В четвертой главе пособия рассматриваются основные понятия теории информации и дискретных систем обработки информации.

Пятая глава пособия посвящена анализу помехоустойчивых кодов, их классификации и сравнительным оценкам, на примере двоичных кодов, наиболее часто встречающихся в практике при проектировании и эксплуатации дискретных устройств.

В шестой главе пособия обобщены вопросы импульсных и цифровых методов передачи непрерывных сигналов.

В седьмой главе пособия анализируются методы передачи сигналов в условиях помех, решаются вопросы защиты каналов от замираний, межсимвольной интерференции и сосредоточенных помех, при передаче различных видов сообщений.

В восьмой главе пособия описываются физические явления и процессы, лежащие в основе многоканальной связи, вопросы объединения и разделения каналов, а также принципы построения систем множественного доступа и протоколы их реализации.

В девятой главе пособия рассмотрены вопросы оценки эффективности систем связи при заданной помехоустойчивости.

В десятой главе изложены классические методы шифрования и современные криптологические методы, алгоритмы, протоколы и системы как методы и средства защиты информации в компьютерных системах и системах связи.

Работа по написанию пособия распределилась следующим образом:

Главы 1 (кроме пп. 1.2.4, 1.6.2, 1.7), 2, 3 (кроме п. 3.1) написаны В. А.

Глушковым, глава 4 — А. Г. Нестеренко, пп. 1.7, 3.1 — К. К. Васильевым, главы 6, 7 (кроме § 7.5), пп. 5.1, 5.2 — А. Г. Нестеренко, главы 8 (кроме пп. 8.1.2, 8.1.3), 9

— В. А. Глушковым, глава 10 — А. Г. Нестеренко, пп. 1.2.4, 1.6.2, 7.5, 8.1.2, 8.1.3 —

А. В. Дормидонтовым. Глава 5 (кроме пп. 5.1, 5.2) повторяет материал учебного пособия: Васильев К. К., Новосельцев J1. Я., Смирнов В. Н. Основы теории помехоустойчивых кодов : учеб. пособие. — Ульяновск : УлГТУ, 2000.

Редактирование всех глав пособия выполнено К. К. Васильевым.

studfiles.net

Введение в теорию электрической связи: Учебное пособие

Страницы работы

Фрагмент текста работы

электрической связи, а именно – основ теории информации и теории помехоустойчивости передачи дискретных и непрерывных сообщений.

Пособие рассчитано на студентов 2 – 3 курсов, обучающихся по специальностям «Средства связи с подвижными объектами» и «Многоканальные телекоммуникационные системы» и может быть полезно студентам других направлений и специальностей.

технический университет, 2002

2. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ 6

2.1. Основные понятия и термины 6

2.2. Энтропия и информация 9

2.3. Кодирование источника 16

2.4. Помехоустойчивое кодирование 27

2.5. Информативность непрерывных источников сообщений 38

ВОПРОСЫ И ЗАДАЧИ К РАЗДЕЛУ 40

3. ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ 43

3.1. Основные понятия и термины 43

3.2. Бинарная задача проверки простых гипотез 49

3.3. Приём полностью известного сигнала (когерентный приём) 52

3.4. Согласованная фильтрация 57

3.5. Потенциальная помехоустойчивость когерентного приёма 63

3.6. Некогерентный приём 67

3.7. Потенциальная помехоустойчивость некогерентного приёма 72

ВОПРОСЫ И ЗАДАЧИ К РАЗДЕЛУ 75

4. ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ 76

4.1. Основные понятия и термины 76

4.2. Оптимальное оценивание параметров сигнала 77

4.3. Оптимальная фильтрация случайного сигнала 85

ВОПРОСЫ К РАЗДЕЛУ 88

5. ЦИФРОВАЯ ПЕРЕДАЧА НЕПРЕРЫВНЫХ СООБЩЕНИЙ 89

5.1. Основные понятия и термины 89

5.2. Импульсно-кодовая модуляция 90

5.3. Кодирование с предсказанием 93

ВОПРОСЫ К РАЗДЕЛУ 95

1. ВВЕДЕНИЕ

Системы связи предназначены для передачи информации. Информация передается посредством сообщений. Примерами сообщений могут служить текст телеграммы, фраза в телефонном разговоре, последовательность цифр в сетях передачи данных, изображение в системе фототелеграфии и т.п. Для передачи сообщения необходим материальный носитель, называемый сигналом. Чаще всего в качестве сигналов используют электрические колебания благодаря удобству их генерирования и преобразования. Современная система связи представляет собой сложную совокупность устройств, выполняющих преобразования сообщений и сигналов с целью наиболее эффективной передачи информации. К показателям эффективности относятся достоверность и скорость передачи информации, а также некоторые другие величины. Упрощенная схема системы передачи информации (системы связи) показана на рис. 1.

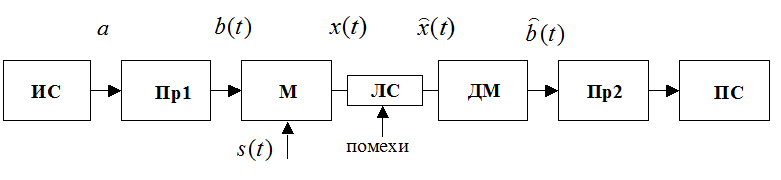
Рис. 1. Упрощенная структура системы связи

Само назначение системы связи предполагает наличие источника и получателя сообщений. Источник ИС порождает сообщение 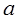, которое преобразуется преобразователем Пр1 в сигнал 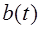, называемый первичным сигналом. Первичный сигнал, как правило, непригоден для непосредственной передачи, поэтому он поступает на модулятор М, где используется для модуляции другого колебания 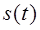, более подходящего для передачи и называемого переносчиком или несущим колебанием. Модулированный сигнал 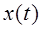поступает в линию связи ЛС, в которой происходит его искажение под влиянием характеристик линии, а также неизбежное воздействие на сигнал вредных колебаний (помех). Сигнал 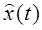, поступающий с выхода линии связи на демодулятор ДМ, отличается от переданного сигнала 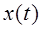, поэтому вырабатываемый демодулятором сигнал 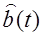в общем случае отличается от первичного сигнала 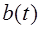. Качество демодулятора тем выше, чем меньше это отличие. Сигнал 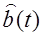преобразуется преобразователем Пр2 в сообщение 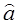, передаваемое получателю сообщения ПС.

Рассмотренная структура системы связи является простейшей и сравнительно редко применяется на практике. В реальных современных системах связи для повышения скорости и достоверности передачи используются дополнительные преобразования, такие как кодирование и декодирование. Кроме того, сигналы часто передаются по линиям связи, имеющим различную физическую природу (например, электрический сигнал преобразуется в оптический и обратно) и различные характеристики, поэтому сигнал в процессе передачи многократно меняет свои свойства. Совокупность устройств и линий связи, которые сигнал проходит последовательно между любыми двумя точками системы связи, называется каналом связи.

2. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

2.1. Основные понятия и термины

Информация относится к предельно широким понятиям, которым

vunivere.ru

ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ

Транскрипт

1 Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ» ПРОГРАММА, МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ по дисциплине ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ Часть I для студентов заочной формы обучения специальности Сети телекоммуникаций Минск 2004

2 Составитель Черная И.И. Приведены программа, методические указания по самостоятельному изучению первой части дисциплины, вопросы для самопроверки, а также задания на домашнюю контрольную работу и методические указания по ее выполнению. Рецензент Клюев Л.Л.

3 ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ В дисциплине изучаются основные закономерности и методы передачи информации по каналам связи; рассматриваются способы математического представления сообщений, сигналов и помех, методы формирования сигналов и их преобразования в каналах связи, вопросы анализа помехоустойчивости и пропускной способности систем связи, оптимального приема сообщений и оптимизации систем связи. Программа и методические указания по изучению дисциплины для студентов заочной формы обучения уровня высшего образования составлены в 3 частях. Каждая часть охватывает материал учебной программы одного семестра. Изучение дисциплины целесообразно сопровождать составлением конспекта. После изучения раздела программы следует занести в конспект ответы на вопросы для самопроверки, решения задач и др. При выполнении контрольных работ необходимо руководствоваться методическими указаниями и рекомендованной литературой. Контрольные работы должны быть оформлены в соответствии с требованиями стандартов, а также следующих правил: 1. Прежде чем выполнять какой-либо расчет, необходимо указать его цель, дать ссылку на источник, откуда взяты расчетные соотношения (номер литературы по списку и номер формулы). 2. Привести формулу, подставить в нее числовые значения известных величин, привести результаты промежуточных вычислений и конечный результат. В промежуточных вычислениях размерности величин не указываются; в конечном результате приведение размерности обязательно. 3. Все расчеты необходимо выполнять в стандартных единицах Международной системы единиц СИ с точностью до третьей значащей цифры. 4. Определение векторных величин следует сопровождать рисунком и указанием направления векторов. 5. Графики необходимо строить на миллиметровой бумаге с указанием масштаба, размерности величин и расчетных точек. 6. В конце работы следует привести список использованной литературы и расписаться. Вариант заданий определяется двумя последними mп цифрами номера студенческого билета и номером группы р на потоке ( m предпоследняя; а п — последняя цифры номера студенческого билета).

4 ПРОГРАММА И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ 1 Обобщенный ряд Фурье Детерминированные сигналы. Аналоговые, дискретные и цифровые сигналы. Нормированное пространство сигналов. Ортогональные сигналы. Ортонормированный базис. Разложение сигнала в обобщенный ряд Фурье по выбранному базису. Содержание темы связано с анализом сигналов, соответствующих известным на приемном конце сообщениям. Такие сигналы называются детерминированными. Применение детерминированных сигналов оказывается полезным при решении задач линейных и нелинейных преобразований и при оценке искажений сигналов при их прохождении через линейные и нелинейные цепи. Определение детерминированных сигналов дано в [1] и [3]. Всякий сигнал может быть представлен в виде вектора. Длина вектора называется его нормой. Если сигналы образуют пространство, где каждому его вектору соответствует определенная норма, то такое пространство сигналов называется нормированным. Два сигнала u и U называются ортогональными, если их скалярное произведение равно 0. Скалярное произведение двух сигналов вычисляется по формуле ( u, U ) = u( t) U ( t) dt Если для каждых двух сигналов из бесконечной системы функций , ортогональных друг другу и существующих на отрезке [t 1, t 2 ] справедливо равенство 1, если i = j (u,u) = 0, если i j, то говорят, что они обладают единичными нормами. Ортогональные сигналы с единичными нормами образуют ортонормированный базис. Любой сигнал S(t), принадлежащий этому пространству, можно разложить в ряд по выбранному базису

5 i= 0 S ( t) = CU i i( t). Это представление сигналов называется обобщенным рядом Фурье. Для представления сигналов используются базисные функции sin x, по- x линомы и функции Лежандра, Чебышева, Лагерра и Эрмита. Для представления дискретных сигналов функции Хаара, Радемахера и Уолша. Из приведенных базисных функций важными являются функции строится ряд Котельникова. sin x, на основе которых x Материал данной темы можно изучить в [3], с , с ; [1], с , 36 39; [6], с Вопросы для самопроверки 1. Что понимают под детерминированным сигналом? 2. Что такое норма сигнала? 3. Что называют нормированным пространством? 4. Как вычисляется скалярное произведение сигналов? 5. Дайте определение ортогональным сигналам. 6. Какие сигналы образуют ортонормированный базис? 7. Какой формулой определяется обобщенный ряд Фурье? 8. По какой формуле определяются коэффициенты обобщенного ряда Фурье? 9. Какие базисные функции используются для представления сигналов? 10. Что собой представляет система функций Уолша?

6 2 Ряды Фурье Ряд Фурье в комплексной форме. Коэффициенты ряда Фурье. Дискретный спектр сигнала. Ряд Фурье в тригонометрической форме. Спектр амплитуд и спектр фаз. Вычисление спектральных коэффициентов. Если в качестве базисных функций выбраны периодические экспоненциальные функции, то мы получим ряд Фурье в комплексной форме (формулы (2.6) и (2.7) из [1], и (2.11) и (2.12) из [3]).Формулы (2.7) из [1] и (2.12) из [3] служат для определения коэффициентов ряда Фурье. Совокупность этих коэффициентов отображает спектр сигнала. Спектр сигнала представляет собой разложение сигнала на отдельные составляющие по частоте. Периодические сигналы имеют дискретные (линейчатые) спектры. Модуль спектра сигнала характеризует спектр амплитуд этого сигнала, а аргумент — спектр фаз. Если преобразовать по формуле Эйлера экспоненциальные функции в тригонометрические, то мы по получим ряд Фурье в тригонометрической форме, где роль базисных функций будут играть гармонические сигналы. В этом случае для расчета спектральных коэффициентов ряда Фурье используются формулы (2.11) и (2.12) из [1] и (2.5) и (2.6) из [3]. В этой литературе также даны примеры вычисления коэффициентов ряда Фурье, с которыми следует подробно ознакомиться. Содержание этой темы изложено в [1], с ; [3], с ; [6], с Вопросы для самопроверки 1. Какие функции являются базисными при представлении сигнала в виде ряда Фурье в комплексной и тригонометрической формах? 2. Как записать ряд Фурье в комплексной форме? 3. Какой формулой определяются коэффициенты ряда Фурье в комплексной форме? 4. Что такое спектр сигнала? 5. Какие сигналы имеют дискретные спектры?

7 6. Что такое спектр амплитуд и спектр фаз? 7. Как записать ряд Фурье в тригонометрической форме? 8. По каким формулам рассчитываются спектральные коэффициенты ряда Фурье в тригонометрической форме? 3 Интеграл Фурье Спектральная плотность сигнала. Прямое и обратное преобразования Фурье. Спектр непериодического сигнала. Свойства спектральной плотности. Дельта-импульс и его свойства. Построение спектров видеосигналов и модулированных сигналов. Спектральная плотность — это комплексная функция, представляющая амплитуду напряжения (тока), приходящуюся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту f. Спектральная плотность S(jω) и сигнал S(t) взаимно однозначно связаны между собой парой преобразований Фурье. Необходимо хорошо запомнить и уметь использовать эти выражения ([1], формулы (2.14) и (2.15) и [3], формула (2.19)). Необходимо изучить основные свойства спектральной плотности: изменение спектральной плотности при сдвиге сигнала во времени, при изменении масштаба времени, при дифференцировании и интегрировании сигнала, при сложении сигналов (суммирование спектров), при перемножении сигналов (свертка спектров) [1], с ; [3], с ; [6], с Большую роль в спектральном анализе играет единичный импульс, у которого амплитуда стремится к бесконечности, а длительность стремится к нулю. Математической моделью такого сигнала является δ-функция Дирака [1], с. 26; [3], с ; [6], с Важным свойством δ-функции является фильтрующее свойство. Это свойство используется при расчете спектров модулированных сигналов. Примеры построения спектров различных сигналов приведены в [1],с ; [3],с. 47, ,

8 Спектр одиночного прямоугольного видеоимпульса является сплошным, имеет лепестковую структуру с амплитудой, убывающей по закону sin x. Спектр x модулированного сигнала представляет собой спектр сигнала модулирующего, перенесенный на частоту несущей, и вычисляется как свертка их спектральных плотностей [1], с. 52; [3], 55. Вопросы для самопроверки 1. Запишите формулы прямого и обратного преобразования Фурье и поясните их смысл. 2. Дайте определение понятия спектральная плотность. 3. Чем отличаются спектры периодических и непериодических сигналов? 4. Что собой представляет δ-импульс? 5. Какие свойства имеет δ-функция? 6. Перечислите основные свойства спектральной плотности. 7. В каких случаях применяется свертка спектров сигналов? 8. Какой вид имеет спектр гармонических сигналов? 9. Как выглядит спектр модулированного импульса? 4 Характеристики сигнала Энергия сигнала. Равенство Парсеваля. Спектральная плотность мощности сигнала. Автокорреляционная функция сигнала. Связь автокорреляционной функции со спектральными характеристиками сигнала. Под энергией сигнала понимают величину Е = u 2 ( t) dt Ее можно также выразить через спектральную плотность энергии (или энергетический спектр), которая определяется равенством Парсеваля. Если рассмотреть сигнал, существующий на ограниченном интервале времени [-τ/2; τ/2] и разделить на период Т обе части этого равенства, устремив Т к.

9 бесконечности, то получим предел, называемый спектральной плотностью мощности G(ω) см. [1], с ; [3], с ; [6], с. 36. Автокорреляционной функцией сигнала называется скалярное произведение сигнала на его сдвинутую копию. Автокорреляционная функция (АКФ) сигнала является четной функцией. Эта функция сигнала связана с энергетическим спектром сигнала парой преобразований Фурье. Свойства АКФ следует изучить в [1], с ; [3], с ; [6], с Сигналы с ограниченной энергией (например, одиночный импульс или пачки импульсов) имеют максимальное значение АКФ в точке τ=0, которое определяется энергией сигнала. Автокорреляционная функция сигнала с неограниченной энергией связана преобразованиями Фурье со спектральной плотностью мощности и ее максимальное значение определяется не энергией, а средней мощностью сигнала. Неограниченную энергию имеют периодические сигналы, неограниченные во времени [1], с ; [3], с. 77;[6],с Вопросы для самопроверки 1. Как определяется энергия сигнала? Запишите формулу равенства Парсеваля. 2. По какой формуле находится спектральная плотность мощности сигнала? 3. Дайте определение и запишите формулу для расчета АКФ сигнала. 4. Перечислите основные свойства АКФ. 5. Как связана АКФ с энергетическим спектром сигнала? 6. Как связана АКФ со спектральной плотностью мощности сигнала? 7. Какие сигналы имеют неограниченную энергию? 8. Чем отличается АКФ сигнала с ограниченной энергией от АКФ сигнала с неограниченной энергией?

10 5 N-мерное и функциональное пространство Понятие векторного пространства. Свойства n-мерного пространства. Функциональное пространство Гильберта. Выражение скалярного произведения спектральных плотностей через формулу свертки. При решении ряда задач, связанных с анализом и преобразованием сигналов, целесообразно отображать эти сигналы векторами некоторого векторного пространства. Свойства n-мерного пространства являются обобщением свойств двумерного. Длина n-мерного вектора u u, u. u ) определяется его нормой. ( 1 2 n Расстояние между двумя n-мерными векторами n d( u, υ) = u υ = ( υ ) i= 1 Скалярное произведение двух n-мерных векторов n u υ = u i υi. i= 1 Развитием понятия векторного пространства является функциональное пространство. Норма функции u(t) определяется: u i u ( t) = u( t) dt, T 2 T 2 где Т интервал времени, на котором определена функция u (t). Расстояние между функциями u (t) и υ (t) равно норме разности T [ u( t) υ( t) ] u( t) υ ( t) = dt. 2 T 2 Скалярное произведение функций u (t) и υ (t) определяется как число T 2 ( u, υ ) = u( t) υ( t) dt. T 2 Пространство функций с такой нормой и таким скалярным произведением называется функциональным пространством Гильберта. Скалярное произведение спектральной плотности сигнала υ (t) на сдвинутое по частотной оси зеркальное отображение спектральной плотности сигнала i 2 2.

11 u (t) выражается известной формулой свертки и называется сверткой спектров, [1], с. 35. Материал для изучения данной темы изложен в [1], с ; [2], с ; [3], с Вопросы для самопроверки 1. В чем отличие между нормами n-мерного и гильбертового пространства? 2. Какой формулой выражается расстояние между двумя n-мерными векторами? 3. Как записать скалярное произведение двух n-мерных векторов? 4. Как записывается выражение для расстояния между двумя функциями времени? 5. Какой формулой выражается скалярное произведение двух функций? 6. Что такое свертка спектров? 6 Квазигармоническое представление сигналов Комплексное и квазигармоническое преобразования сигналов. Преобразование Гильберта. Аналитический сигнал. Сопряженный сигнал и его физический смысл. Узкополосный сигнал. Часто при анализе сигнала его записывают в виде комплексной функции времени и используют такие понятия как огибающая сигнала, мгновенная фаза, мгновенная частота. Если действительная и мнимая части комплексной функции времени составляют пару преобразований Гильберта, то такой сигнал называется аналитическим [3], формулы (5.45) и (5.46). Для аналитического сигнала огибающая и мгновенная фаза однозначно определяются по формулам (5.56) и (5.57) из [3]. Аналитический сигнал может быть записан в виде где s (t) вещественный сигнал,

s ( t) s( t) + js ( t) =, s мнимая часть аналитического сигнала.

t Сигнал s ( ) называется сопряженным по отношению к исходному s (t). Физический смысл этого понятия заключается в следующем: чтобы получить сопряженный сигнал нужно осуществить поворот фаз всех спектральных составляющих на угол 90 0 в области положительных частот и на угол 90 0 в области отрицательных частот, не изменяя их по амплитуде. Комплексное представление сигнала (см. формулу (2.70) из [2]) позволяет записать этот сигнал в квазигармонической форме (см. формулу (2.72) из [2]). Выражением (2.72) пользуются при анализе частотно-избирательных цепей с ограниченной шириной полосы пропускания. Если эта ширина невелика по сравнению с несущей частотой, то выходной сигнал называется узкополосным. Узкополосный сигнал является квазигармоническим, т.е. почти гармоническим колебанием, у которого огибающая и фаза являются медленно меняющимися функциями времени. Необходимые сведения по данной теме изложены в [1], с ; [2], с ; [3], с Вопросы для самопроверки 1. Как записывается выражение для сигнала в комплексной форме? 2. Какие формулы однозначно определяют аналитический сигнал? 3. Запишите прямое и обратное преобразования Гильберта. 4. Перечислите основные свойства преобразований Гильберта. 5. Что такое сопряженный сигнал и каков его физический смысл? 6. Как выглядит характерная осциллограмма узкополосного сигнала? 7. Какие математические выражения определяют огибающую, фазу и мгновенную частоту сигнала? 7 Дискретное преобразование Фурье Математическая модель дискретизированного сигнала. Прямое и обратное дискретное преобразование Фурье. Свойства дискретного преобразования Фурье. Дискретные преобразования Фурье (ДПФ) являются важными математическими моделями дискретных сигналов. Формулы, определяющие прямое и об-

13 ратное дискретные преобразования Фурье являются аналогами формул для ряда Фурье в комплексной форме и вытекают из последних. Поскольку ряд Фурье в комплексной форме определяет периодически повторяющийся аналоговый сигнал, то и ДПФ определяет периодически повторяющийся дискретный сигнал. Выборки, взятые через интервал дискретизации Δ в течение одного периода Т сигнала, определяют спектральные коэффициенты С к прямого ДПФ, которые повторяются с периодом N = T/Δ. Обратное ДПФ определяет периодически повторяющиеся выборки U(n) (период выборок равен N) через спектральные коэффициенты С к. После изучения этой темы необходимо уметь пользоваться формулами прямого и обратного ДПФ, а также знать свойства ДПФ. Материал для изучения данной темы изложен в [1], с ; [3], с Вопросы для самопроверки 1. Дискретный сигнал на интервале периодичности задан с помощью 8 отсчетов. Какой номер имеет наивысшая спектральная компонента, входящая в формулу обратного ДПФ? 2. Сформулируйте свойства ДПФ. В чем практическая ценность свойств ДПФ? 3. Используя формулу обратного ДПФ, докажите справедливость равенства U(n)=U(n+N), где U(n) n-й отсчет; U(n+N) (n+n)-й отсчет сигнала U(t), N период дискретного сигнала. 4. Используя фомулу прямого ДПФ, докажите справедливость равенства С к = С N+к, где С к, С N+к повторяющиеся с периодом N спектральные коэффициенты ДПФ. 8 Быстрое преобразование Фурье Невозможность использования ДПФ в реальном масштабе времени. Алгоритм быстрого преобразования Фурье. Операция бабочка. Использование

14 прямого и обратного быстрого преобразования Фурье в системах обработки сигналов. Для вычисления ДПФ и обратного ДПФ последовательности из N элементов требуется выполнить N 2 операций с комплексными числами. Для больших массивов информации получается значительный объем вычислений. Сократить число выполняемых операций позволяет алгоритм быстрого преобразования Фурье (БПФ). Вычисления строят по итерационному принципу: последовательности отсчетов с четными и нечетными номерами вновь разбивают на две части. Процесс продолжается до тех пор, пока на получиться последовательность, состоящая из единственного элемента. В основе алгоритма лежит базовая операция: сложение-вычитание с умножением одного из слагаемых на коэффициент n W N, называемой операцией бабочка. Эта операция позволяет построить сигнальный граф при заданном числе N. Применение БПФ позволяет снизить число операций до Nlog 2 N. Это обусловило его широкое применение в области цифровой фильтрации сигналов. Материал для изучения данной темы приведен в [3], с ; [6], с Z преобразование Определение и свойства Z преобразования. Обратное Z преобразование. Связь Z преобразования с преобразованиями Лапласа и Фурье. Применение Z преобразования. Z преобразование играет по отношению к дискретным сигналам такую же роль, как интегральные преобразования Фурье и Лапласа по отношению к непрерывным сигналам. Каждой числовой последовательности =, соответсвующей, k 0 1 u m выборочным значениям сигнала, можно поставить в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной u( z) = k= 1 u k z k

15 Преобразование Лапласа при определенных условиях переходит в Z преобразование и преобразование Фурье может переходить в Z преобразование. Z преобразование как и преобразование Фурье обладает свойством линейности, умножается на z -1 при сдвиге дискретной последовательности вправо на одну позицию, а также подлежит свертке с другим Z преобразованием при перемножении соответствующих им сигналов. Существует также обратное Z преобразование u 1 m 1 m = z U ( z) dz 2πj Z преобразование используется при анализе цифровых фильтров (в частности, для нахождения импульсной характеристики и частотного коэффициента передачи). Материал для изучения данной темы изложен в [1], с ; [3], с ; [6], с Вопросы для самопроверки 1. Что такое Z преобразование? 2. Какую роль играет Z преобразование при анализе дискретных последовательностей? 3. Запишите формулы прямого и обратного Z преобразования. 4. Перечислите важнейшие свойства Z преобразования. 5. Как связано Z преобразование с преобразованиями Лапласа и Фурье? 6. Где используется Z преобразование? 10 Модуляция шумоподобного сигнала Дискретная модуляция постоянного тока. Модуляция шумоподобного сигнала по форме. Амплитудная и фазовая модуляция шумоподобного сигнала. Модуляторы шумоподобного сигнала и их структурные схемы. Преимущества использования шумоподобного сигнала.

16 Дискретная модуляция постоянного тока используется в цифровых системах передачи. Существует две разновидности дискретной модуляции постоянного тока: модуляция по амплитуде и модуляция по знаку. Модуляторы постоянного тока используются для получения шумоподобных сигналов. Модуляция шумоподобного сигнала по форме осуществляется следующим образом. Сообщение в виде двоичного кодового слова разбивается на блоки длиной в к символов. Набору 2 к =1, 2, 3, двоичных кодовых слов каждого блока ставится в однозначное соответствие набор отличающихся по форме шумоподобных сигналов (ШС). Частными случаями этой модуляции являются: амплитудная модуляция шумоподобного сигнала и фазовая модуляция шумоподобного сигнала. Для амплитудной модуляции и фазовой модуляции шумоподобных сигналов длина блоков равна единице (к=1), а число возможных форм равно двум. Структурные схемы генераторов и модуляторов шумоподобных сигналов можно изучить по [1], с Помеха, создаваемая шумоподобным сигналом пренебрежимо мала. В системах с шумоподобными сигналами можно обеспечить высокий уровень скрытности передачи сигналов. Материал для изучения данной темы изложен в [1], с ; [2], с Вопросы для самопроверки 1. Где используется дискретная модуляция постоянного тока? 2. Как получить шумоподобный сигнал? 3. Каков принцип формирования шумоподобного сигнала по форме? 4. Приведите структурную схему и диаграммы, поясняющие работу амплитудного модулятора шумоподобного сигнала. 5. Приведите структурную схему и диаграммы, поясняющие работу фазового модулятора шумоподобного сигнала. 6. В чем преимущество системы передачи с шумоподобными сигналами?

17 11 Детектирование шумоподобных сигналов Особенности детектирования шумоподобных сигналов. Детектирование амплитудно-модулированных(ам) и фазо-модулированных(фм) шумоподобных сигналов. Одноканальный детектор. Детектирование шумоподобных сигналов по форме. Структурная электрическая схема многоканального когерентного детектора. Тактовая синхронизация при приёме видео- и радио- шумоподобных сигналов. Основным способом детектирования шумоподобных сигналов является когерентный. Детектор АМ и ФМ шумоподобного сигнала является одноканальным. При детектировании модулированного по форме шумоподобного сигнала детектор является многоканальным. При детектировании модулированный шумоподобный сигнал умножается или на одну копию шумоподобного сигнала переносчика при АМ и ФМ, или на 2 k копий при модуляции шумоподобного сигнала по формуле (где k длина блока). Далее производится фильтрация одним или несколькими фильтрами нижних частот, которые определяют напряжение на выходе детектора. При приеме видео- и радиосигналов нужно подстраивать тактовую частоту, задержку опорных сигналов и несущую частоту принимаемого сигнала. Это осуществляется устройствами тактовой синхронизации, поиска и слежения во времени и по несущей частоте. Изучение данной темы рекомендуется провести по [1], с Вопросы для самопроверки 1. Как осуществляется детектирование АМ и ФМ шумоподобного сигнала? 2. Нарисуйте структурную электрическую схему и временную диаграмму, поясняющую детектирование АМ и ФМ шумоподобного сигнала. 3. Как осуществляется детектирование модулированных по форме шумоподобных сигналов?

18 4. Нарисуйте структурную электрическую схему и временную диаграмму, поясняющую детектирование модулированного по форме шумоподобного сигнала. 5. Какова роль ФНЧ в детекторах шумоподобных сигналов? 6. Как осуществляется подстройка параметров опорных шумоподобных сигналов под параметры принимаемого сигнала? 12 Случайные сигналы и их математические модели Сигналы как случайные процессы. Ансамбль реализаций. Функция распределения и плотность распределения вероятности. Моментные функции случайного процесса. Стационарный случайный процесс в узком и широком смыслах слова. Эргодический случайный процесс. Математические модели непрерывных и дискретных случайных процессов. Случайный процесс это особого вида функция, характеризующаяся тем, что в любой момент времени принимаемые ею значения являются случайными величинами. Фиксируя на определенном промежутке времени мгновенные значения случайного сигнала, получаем одну реализацию случайного процесса. Случайный процесс представляет собой бесконечную совокупность таких реализаций, образующих статистический ансамбль. Важнейшими характеристиками случайного процесса являются: интегральная функция распределения и плотность распределения вероятности. Удобными числовыми характеристиками случайного процесса являются моментные функции: математическое ожидание, дисперсия и функция корреляции (формулы (4.7), (4.9), (4.10) в [1] или (6.43), (6.44), (6.45) в [3]). Случайный процесс называется стационарным, если его статистические характеристики одинаковы во всех сечениях. Случайный процесс стационарен в узком смысле, если его любая n-мерная плотность вероятности инвариантна относительно временного сдвига. Случайный процесс стационарен в широком смысле, если его математическое ожидание и дисперсия не зависят от времени, а функция корреляции зависит лишь от разности τ = t 2 t 1.

19 Стационарный случайный процесс называется эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени. Эргодические процессы чаще других используются в качестве математических моделей сообщений, сигналов и помех. Случайные процессы могут быть дискретными. Математическими моделями дискретных процессов являются случайные последовательности. Наиболее простой моделью является случайная последовательность с независимыми дискретными значениями, которая описывает сообщение дискретного источника без памяти. Если же имеет место статистическая зависимость между значениями случайного процесса в моменты времени t 1, t 2,,t N, то такой дискретный случайный процесс называется дискретным процессом с памятью. Если статистическая зависимость имеет место только между значениями процесса в соседние моменты времени, то такой дискретный случайный процесс называется простым марковским процессом. Сведения по содержанию данной темы приведены в [1], с ; [2], с ; [3], с ; [6], с Вопросы для самопроверки 1. Что такое случайный процесс? 2. Что такое реализация и ансамбль реализаций? 3. Какие основные характеристики случайного процесса Вы знаете? 4. Какие моментные функции чаще всего используются для характеристики случайных процессов? 5. Что такое стационарный случайный процесс? 6. Дайте определение стационарному случайному процессу в узком и широком смыслах. 7. Какие случайные процессы называются эргодическими? 8. Какие математические модели случайных процессов Вы знаете? 9. В чем различие дискретных случайных процессов без памяти и с памятью?

20 13 Нормальные случайные процессы Определение нормального или гауссовского случайного процесса. Плотность вероятности и функция распределения нормального случайного процесса. Функция корреляции нормального случайного процесса. Белый шум. Свойства белого шума. Нормальным или гауссовским случайным процессом называется такой процесс, n-мерная плотность распределения вероятности которого определяется формулой (4.29), [1]. Нормальный случайный процесс занимает особое место при анализе систем связи. Он чаще, чем другие законы встречается на практике. Примерами случайного процесса с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Полезные сигналы, являющиеся суммой большого числа независимых случайных элементарных сигналов, например, гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гауссовские случайные процессы. Основные характеристики гауссовских случайных процессов определяются формулами (6.9), (6.10), [3] и (4.35), [1]. Эргодический центрированный стационарный нормальный процесс, корреляционная функция которого равна δ функции, а спектральная плотность мощности постоянна на всех частотах, называется белым шумом. Дисперсия белого шума равна бесконечности. Материал для изучения данной темы изложен [1], с ; [3], с , , 155; [6], с Вопросы для самопроверки 1. Что называется нормальным (или гауссовским) случайным процессом? 2. Приведите примеры случайных процессов с гауссовским распределением. 3. Какие основные характеристики гауссовских случайных процессов Вы знаете? 4. Что называется белым шумом? 5. Приведите формулы для расчета основных параметров белого шума.

21 14 Узкополосные случайные процессы Определение узкополосного случайного процесса. Огибающая и фаза узкополосного случайного процесса. Дисперсия узкополосного случайного процесса. Плотность распределения огибающей и фазы узкополосного случайного процесса. Закон Релея. Плотность распределения огибающей смеси узкополосного случайного шума и гармонического сигнала. Закон Райса. Случайный процесс называется узкополосным, если ширина его спектра относительно мала по сравнению со средней частотой этого спектра. Подобные процессы возникают, например, на выходах линейных частотно-избирательных многокаскадных усилителей при действии на их входах теплового шума. Функция корреляции, огибающая и фаза узкополосного случайного процесса определяются по формулам: (7.38), (7.40), (7.44), (7.45), [3]. Плотность распределения вероятности огибающей и фазы узкополосного случайного процесса определяется по формулам (4.43), [1] и (7.60), (7.61), [3]. Закон распределения плотности вероятности огибающей узкополосного случайного процесса называется законом Релея. Плотность вероятности огибающей смеси узкополосного случайного шума и гармонического сигнала распределяется по закону Райса и определяется формулами (4.44), [1] и (7.78), [3]. Изучение темы можно провести по [1], с ; [3], с ; [2], с ; [6], с Вопросы для самопроверки 1. Что называется узкополосным случайным процессом? 2. Какие основные параметры узкополосного случайного процееса Вы знаете? 3. Распределение какой характеристики отображает закон Релея? 4. Нарисуйте график распределения Релея и поясните его физический смысл. 5. Распределение какой характеристики отображает закон Райса? 6. Нарисуйте график распределения Райса и поясните его физический смысл.

22 Контрольная работа 1 Задача 1 1. Запишите формулы для расчета спектральных коэффициентов ряда Фурье в тригонометрической форме. 2. Вычислите спектральные коэффициенты для сигналов, приведенных на рис. 1. Интервал разложения равен [-τ/2; τ/2]. Число спектральных коэффициентов n = 5. а) а) б) Рис. 1 Временные диаграммы Исходные данные сигналов Таблица 1 Параметры Номер варианта сигнала Рис. 1,а Длительность импульса τ, мс , Номер варианта Рис. 1,б Длительность импульса τ, мс ,8 4,6 10, ,4 2,8 10,4 5,8 12 mn Примечание: Амплитуду импульсов А m принять равной 0,5 p 2 +, В. Методические указания по выполнению задачи 1 Для выполнения задачи следует изучить [1], с ; [3], с ; [5], с , , 185. Аналитическое выражение для сигнала на рис. 1,а: 2t нала на рис. 1,б: u( t) = A m 1. τ πt u( t ) = A cos m, для сиг- τ

23 Задача 2 1. Для сигнала u(t) (табл. 2) с параметрами (табл.3) найти спектральную плотность и амплитудный спектр сигнала. 2. Постройте временную и спектральную диаграммы сигнала. Исходные данные Номер варианта Аналитическое выражение сигнала u(t) cosω t A m 0 Таблица A m, τ/2 > t > — τ/2 0, -τ/2 > t > τ/2 (1) A m sinω 0 t A m ( t)cosω 0 t ( A m (t) задано формулой (1)) a0 + ( a cos kω t + b sin kω t) k 1 k 2 k = 1 A m 1+ mcosωt cosω [ ] t Исходные данные 1 Таблица 3 Параметры Номер варианта сигнала τ, мкс f 0, кгц Номер варианта f 0, кгц a k, В Τ, мс m 0,5 0,9 0,8 0,4 0,7 F, кгц Примечание: Амплитуду сигнала по вариантам принять равной mn + 0,5 p. Постоянную составляющую по вариантам принять равной 2 mn p. 4 Методические указания по выполнению задачи 2 Для решения задачи необходимо изучить [1], с ; [3], с ; [6], с

24 Задача 3 1. Дайте определение автокорреляционной функции (АКФ) сигнала и запишите формулу для её расчета. 2. Для заданного сигнала u(t) (табл. 4) с параметрами (табл. 5) определите АКФ одним из предложенных способов. Исходные данные Таблица 4 Номер Вид сигнала u(t) Способ представления варианта АКФ Аналитический Аналитический и графический Аналитический u(t) Графический Am τ. 0 Τ t Графический

25 Исходные данные Таблица 5 Параметры Номер варианта сигнала τ, мс 6 2, ,5 2,8 7 8,5 6,2 2 4, Номер варианта τ, мс 10, ,2 3, ,6 7 Т, мс ,4 6, ,2 14 mn p Примечание: амплитуду сигнала принять равной. 2 4 Методические указания по выполнению задачи 3 Для решения задачи следует изучить [1], с ; [3], с ; [6], с Полезно рассмотреть пример [1], с. 29. Он показывает, как получить АКФ в виде аналитического выражения и в виде графика. Для вариантов целесообразно изучить [6], с , где показано, как найти периодическую и непериодическую АКФ. При этом можно воспользоваться готовым аналитическим выражением и построить график АКФ. Задача 4 1. Приведите формулу для определения энергии. 2. Определите энергию сигнала u(t) (табл. 6) с параметрами, приведенными в табл. 7. Таблица 6 Исходные данные Номер варианта Сигнал u(t) Интервал времени существования сигнала А m -τ/2 I agree.

docplayer.ru