• 

§ 18. Правила Кирхгофа

Соединения резисторов и источников в сложных цепях не всегда можно свести к совокупности последовательного и параллельного их соединений. Для расчётов сложных цепей удобно применять правила Кирхгофа.

Узлом электрической цепи будем называть точку, где сходятся не менее трёх проводников. Токи, подходящие к узлу, будем считать положительными, а выходящие из узла – отрицательными. Узел – это не обкладки конденсатора, где может происходить существенное накопление заряда. Отсюда следует первое правило Кирхгофа: алгебраическая сумма токов в узле равна нулю.

Участок цепи между двумя узлами называется ветвью. Возьмём в сложной цепи произвольный замкнутый контур, состоящий из отдельных ветвей. Выберем направление обхода контура по часовой стрелке или против. ЭДС в каждой ветви контура будем считать положительной, если направление её действия совпадает с выбранным направлением обхода контура, а в противном случае – отрицательной. Падение напряжения (произведение тока на сопротивление) в любой ветви контура будем считать положительным, если направление тока в этой ветви совпадает с направлением обхода контура, в противном случае – отрицательным. Записав для каждой ветви контура уравнение закона Ома для участка цепи, содержащего ЭДС, и сложив все уравнения, получим второе правило Кирхгофа: в произвольном замкнутом контуре любой электрической цепи сумма падений напряжений во всех ветвях контура равна алгебраической сумме ЭДС во всех ветвях контура.

Оба правила Кирхгофа справедливы не только для постоянных во времени значений всех величин, входящих в соответствующие уравнения, но и для их мгновенных значений.

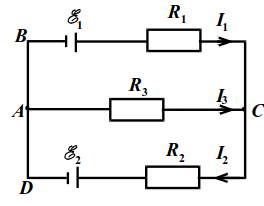
Зададим направления токов произвольно, например так, как показано на рис. 18.1.
Для нахождения трёх неизвестных токов надо составить три независимых уравнения. В схеме n = 2 n=2 узла. По первому правилу Кирхгофа составляем n — 1 = 1 n-1=1 уравнение.

I 1 — I 2 + I 3 = 0 . I_1-I_2+I_3=0.

Недостающие два уравнения составляем по второму правилу Кирхгофа для контуров ABCA и ABCDA: I 1 R 1 — I 3 R 3 = E 1 , I 1 R 1 + I 2 R 2 = E 1 — E 2 . I_1R_1-I_3R_3=_1,\;\;\;\;I_1R_1+I_2R_2=_1-_2.

Решение системы полученных трёх уравнений в общем виде трудоёмко и даёт громоздкие выражения для токов. Систему удобно решать, подставив в неё значения ЭДС и сопротивлений: I 1 — I 2 + I 3 = 0 , 10 I 1 — 45 I 2 = 4 . 2 , 10 I 1 + 10 I 2 = 0 . 4 . I_1-I_2+I_3=0,\;10I_1-45I_2=4.2,\;10I_1+10I_2=0.4.

Решая систему последний трёх уравнений, находим:

I 1 = 0 . 06 A , I 2 = — 0 . 02 A , I 3 = — 0 . 08 A . I_1=0.06A,\;I_2=-0.02A,\;I_3=-0.08A.

Уравнение по правилу кирхгофа

§6. Правила Кирхгофа

Описанные до сих пор методы применимы лишь к схемам, которые можно представить в виде последовательных и параллельных соединений однотипных элементов. Однако большинство встречающихся на практике схем оказываются сложнее. Для их решения применяют два правила Кирхгофа.

Сумма сил всех токов, втекающих в произвольный узел, равна сумме сил всех токов, вытекающих из этого узла.

Напомним, что узел – это точка соединения трёх или более проводов.

Первое правило Кирхгофа является следствием закона сохранения заряда, так как сумма втекающих токов характеризует заряд, приходящий в узел за некоторое время, а сумма вытекающих – заряд, выходящий из узла за то же время. Равенство этих сумм между собой связано с тем, что заряд в узле не накапливается (заряд может накапливаться только на пластинах конденсаторов). Забегая вперёд, отметим, что второе правило Кирхгофа можно рассматривать как следствие закона сохранение энергии.

Перед применением правил Кирхгофа нужно обозначить силы токов в каждой ветви цепи.

Ветвь – это участок цепи между двумя узлами, не содержащий узлов внутри себя. Все элементы одной ветви соединены последовательно, поэтому силы токов через них одинаковы.

Кроме того, нужно обозначить заряды на каждом конденсаторе. Выбор направления тока и выбор, какую из двух обкладок конденсатора считать заряженной положительно, можно делать совершенно произвольным образом. Если выбранное направление тока не совпадёт с фактическим, то просто его сила окажется отрицательной. Если же выбранные знаки зарядов обкладок конденсаторов не совпадут с фактическими, то заряд конденсатора будет отрицательный.

Если применить первое правило Кирхгофа ко всем узлам, то ровно одно из уравнений окажется следствием остальных. Чтобы этого избежать, достаточно придерживаться простого алгоритма: уравнения по первому правилу Кирхгофа следует записать для всех узлов кроме одного (любого).

Для формулировки второго правила Кирхгофа понадобится пара новых определений.

Контур – это замкнутый участок цепи. Чтобы указать контур, нужно, начав с некоторой точки цепи, пройти по какой-либо траектории вдоль элементов цепи и вернуться в исходную точку.

Выбрав контур, необходимо указать направление обхода. Для любого контура их существует ровно два: по часовой стрелке или против. Если контур задан перечислением элементов, то направление обхода определяется их порядком. При выборе контура на схеме удобнее отмечать направление обхода стрелочкой.

Алгебраическая сумма ЭДС источников в произвольном контуре равна алгебраической сумме напряжений на всех остальных элементах этого контура.

Знак каждого из слагаемых в обеих суммах зависит от направления обхода контура и определяется по соответствующим правилам знаков.

Правило знаков для источников. Если направление обхода контура совпадает с направлением действия источника, то перед его ЭДС ставится плюс, иначе – минус.

Правило знаков для резисторов. Если направление обхода контура совпадает с выбранным направлением тока `I` через резистор сопротивлением `R`, то напряжение на резисторе записывается как `U=RI`, иначе `U=-RI`.

Правило знаков для конденсаторов. Напряжение на конденсаторе ёмкостью `C` записывается как `U=q//C`, где `q` — заряд первой встреченной при обходе обкладки конденсатора, в качестве которого может оказаться как `+q`, так и `-q` в зависимости от изначального выбора знаков зарядов на обкладках.

Все перечисленные правила знаков для второго правила Кирхгофа проиллюстрированы на рис. 6.1. Обведённые выражения – это слагаемые, соответствующие конкретному элементу при обходе его слева направо.



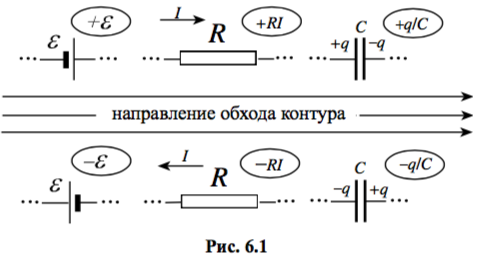
Если применить второе правило Кирхгофа ко всем контурам, то ряд уравнений будут зависимыми, а система – переполненной. Если же какой-то из элементов не войдёт ни в один контур, то система будет неразрешимой. Поэтому для записи уравнений по второму правилу Кирхгофа необходимо выбрать контура так, чтобы каждый элемент входил хотя бы в один из выбранных контуров, а общее число уравнений с учётом записанных по первому правилу Кирхгофа было равно числу неизвестных сил токов, то есть числу ветвей.

Система уравнений, записанная с использованием обоих правил Кирхгофа, является полной, то есть позволяет найти все силы токов и напряжения.

Некоторая страшная схема имеет `u=1024` узла и `v=2009` ветвей. Найдите число `p_2` контуров, к которым придётся применить второе правило Кирхгофа, чтобы найти все силы токов в цепи.

Число `n` уравнений в полной системе равно числу неизвестных сил токов, которое равно числу ветвей: `n=v`. Используя первое правило Кирхгофа, можно записать `p_1=u-1` независимых уравнений. Для записи остальных уравнений потребуется второе правило Кирхгофа, то есть придётся рассмотреть `p_2=n-p_1=v-u+1=986` контуров.

Запишите систему уравнений, с помощью которой можно найти силы всех токов в цепи, схема которой изображена на рис. 6.2. Параметры элементов, отмеченные на рис., известны.



1. Обозначим направления и силы токов во всех ветвях (рис. 6.3).

2. Применим первое правило Кирхгофа для всех узлов:

Легко убедиться, что любое из записанных уравнений является следствием четырёх других, например, последнее уравнение можно получить как сумму остальных, поэтому в систему его можно не включать. Таким образом, не следуя первому алгоритму, мы сделали лишнюю работу.

3. Игнорировать второй алгоритм мы не будем, так как тогда пришлось бы выписать уравнения аж для `17` контуров (читателям предлагается найти все их самостоятельно). Применим второе правило Кирхгофа к четырём контурам (направления обходов обозначены на рис. 6.3 дугами со стрелочками):

4. В итоге мы получим систему из `8` независимых уравнений. Неизвестных сил токов тоже `8`. Система является линейной и имеет единственное решение.

Докажите справедливость формул (5.3) и (5.4) на примере трёх источников постоянного тока.



Выразим `I_1`, `I_2` и `I_3` из последних трёх уравнений:

Подставим полученные выражения в первое уравнение:

Для эквивалентных фрагментов цепи равенство `I_»экв»=I` должно выполняться при любых `R`, что возможно, лишь если

Итак, мы доказали справедливость формул (5.3) и (5.4) в случае трёх источников с одинаковой полярностью. Аналогично можно рассмотреть любой из случаев с различной полярностью источников.

zftsh.online

Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.



где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0



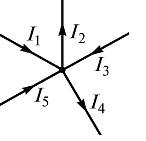
В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре



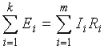
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.



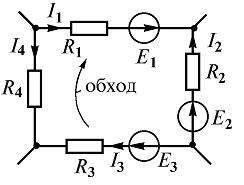
Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.



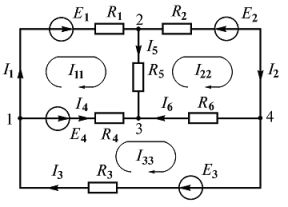
Составляем необходимое число уравнений по первому и второму законам Кирхгофа



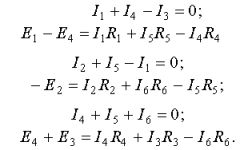
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.

Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.



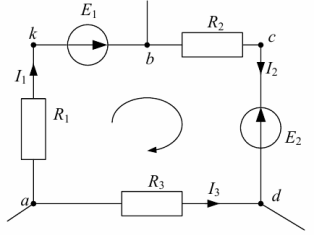
Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).



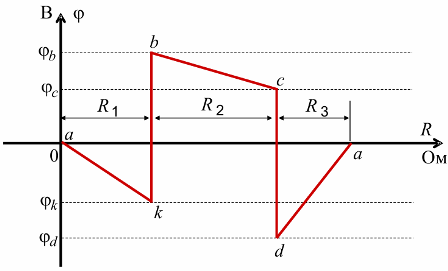
Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»



Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

electricalschool.info

§ 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа





§ 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа. Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы в, число ветвей, содержащих источники тока, — в_ит и число узлов у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется в — в_ит. Перед тем как составить уравнения, необходимо произвольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например по часовой стрелке.

Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют уравнения, число которых равно числу узлов без единицы, т. е. у — 1.

Уравнение для последнего у-го узла не составляют, так как оно совпало бы с уравнением, полученным при суммировании уже составленных уравнений для у — 1 узлов, поскольку в эту сумму входили бы дважды и с противоположными знаками токи ветвей, не подходящих к у-му узлу, а токи ветвей, подходящих к у-му узлу, входили бы в эту сумму со знаками, противоположными тем, с какими они вошли бы в уравнение для у-го узла.

По второму закону Кирхгофа составляют уравнения, число которых равно числу ветвей без источников тока (в — в_ит), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е. (в — в_ит) — (у — 1) = в — в_ит — у + 1.

Составляя уравнения по второму закону Кирхгофа, следует охватить все ветви схемы, исключая лишь ветви с источниками тока.

Если попытаться составить уравнение по второму закону Кирхгофа в форме (2.4) для контура, в который входит источник тока, то в него вошли бы бесконечно большие слагаемые и оно не имело бы смысла.

При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся называть независимыми.

Требование, чтобы в каждый новый контур входила хотя бы одна новая ветвь, является достаточным, но не необходимым условием, а потому его не всегда выполняют. В таких случаях часть уравнений по второму закону Кирхгофа составляют для контуров, все ветви которых уже вошли в предыдущие контуры.





Клещи электроизмерительные

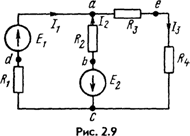
Пример 10. Найти токи в ветвях схемы рис. 2.9, в которой Е₁ = 80 В, Е₂ = 64 В, R₁ = 6 Ом, R₂ = 4 Ом, R₃ = 3 Ом, R₄ = 1 Ом.

Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 2.9, в = 3; в_ит = 0; у = 2.

Следовательно, по первому закону Кирхгофа, можно составить только одно уравнение:

Нетрудно убедиться, что для второго узла получили бы аналогичное уравнение. По второму закону Кирхгофа составим в — в_ит — (у — 1) = 3 — 0 — (2 — 1) = 2 уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.

Знак плюс перед I₁R₁ взят потому, что направление тока совпадает с направлением обхода контура; знак минус перед I₂R₂ — потому, что направление I₂ встречно обходу контура.

Совместное решение уравнений (а) — (в)дает I₁ = 14 А, I₂ = — 15 А, I₃ = — 1 А.

Поскольку положительные направления токов выбирают произвольно, в результате расчета какой-либо один или несколько токов могут оказаться отрицательными. В рассмотренном примере отрицательными оказались токи I₂ и I₃, что следует понимать так: направления токов I₂ и I₃ не совпадают с направлениями, принятыми для них на рис. 2.9 за положительные, т. е. в действительности токи I₂ и I₃ проходят в обратном направлении.

Для выбора контура таким образом, чтобы в каждый из них входило по одной ветви, не входящей в остальные контуры, используют понятие дерева. Поддеревом понимают совокупность ветвей, касающихся всех узлов, но не образующих ни одного замкнутого контура. Из одной и той же схемы можно образовать несколько деревьев. При составлении системы уравнений по второму закону Кирхгофа можно взять любое дерево из возможных.



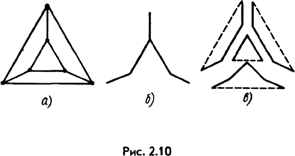
Одно из возможных деревьев схемы рис. 2.10, а изображено на рис. 2.10, б, а на рис. 2.10, в — четыре независимых контура, в каждый из которых входит по одной пунктиром показанной ветви, не входящей в остальные. Более подробно о топологии электрических схем см. § 2.31 — 2.35 и А.5 — А. 10.

www.sonel.ru

Метод уравнений Кирхгофа

Уравнения Кирхгофа являются основными соотношениями, на которых базируются расчеты сложных электрических цепей.

Пусть имеется разветвленная сеть проводов, на различных участках которой находятся генераторы постоянного напряжения и резисторы с известными ЭДС E_k и сопротивлениями R_k ( k = 1, 2, 3,…).Такая сеть называется цепью постоянного тока (рис. 1). Ставится задача: рассчитать токи на каждом участке этой цепи * . Такую задачу можно решить с помощью двух правил (уравнений) Кирхгофа.

Первое правило относится к узлам цепи и утверждает следующее: алгебраическая сумма токов, сходящихся в узле, равна нулю, т. е.

(1)

При этом токам, «входящим в узел», условно приписывается знак «+», а «выходящим» − знак «−». Это правило означает то, что заряды в узле не накапливаются: «сколько входит, столько и выходит»; оно следует из закона сохранения электрического заряда.

Второе правило Кирхгофа относится к любому выделенному в цепи контуру и утверждает следующее: алгебраическая сумма напряжений на всех элементах произвольного контура (кроме генераторов) равна алгебраической сумме ЭДС генераторов, встречающихся в этом контуре, т. е.

(2)

Напряжение и _k = i_kR_k на элементе R_k считается положительным, если выбранное направление обхода данного контура совпадает с выбранной стрелкой тока через данный элемент; ЭДС E_k считается положительной, если выбранное направление обхода контура совпадает со стрелкой ЭДС данного генератора. Это правило следует из основного свойства электростатического поля: циркуляция электростатического поля по любому контуру равна нулю.

Правила Кирхгофа (1) и (2) позволяют написать полную систему линейных алгебраических уравнений, из которой можно однозначно определить токи на всех участках цепи. Практически последовательность составления таких уравнений следующая.

1. На всех участках цепи указать стрелками «направления» токов (стрелки токов наносятся прямо на линию провода). Вообще говоря, стрелки токов можно наносить как попало, их нет нужды угадывать. А вот знаки слагаемых в уравнениях Кирхгофа пишутся уже строго под выбранные стрелки. И если в результате вычислений окажется, что какой-либо ток i_k

* Участком называется фрагмент цепи между двумя узлами, не содержащий других узлов. Узел − это точка цепи, в которой сходятся три или более проводов.

elekt.com.ua