Журнал «Квант»

Заказывайте аудиометры и другое оборудование на сайте компании «МАКСМЕДТЕХ»

Трансформатор

Трансформатор — устройство, служащее для преобразования силы и напряжения переменного тока при неизменной частоте.

Он был изобретен П.Н.Яблочковым в 1878 г., а технический трансформатор впервые создал И.Ф.Усагин в 1882 г.

Работа трансформатора основана на явлении электромагнитной индукции. Простейший трансформатор (рис. 1) представляет собой две изолированные друг от друга катушки (обмотки), намотанные на общий замкнутый сердечник.

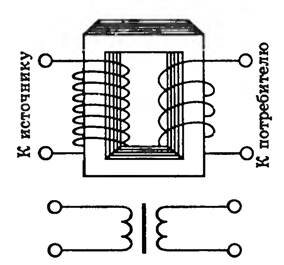
По одной из обмоток (первичной) пропускается преобразуемый переменный ток, а вторичная обмотка соединяется с потребителем. Ток в первичной обмотке создает в сердечнике переменный магнитный поток, который возбуждает ЭДС самоиндукции \(

\varepsilon = -\frac \) в каждом витке первичной катушки (ΔΦ — изменение магнитного потока через один виток за время Δt). Этот же магнитный поток пронизывает витки вторичной катушки и создает в каждом ее витке ЭДС индукции \(

\varepsilon .\) Если первичная обмотка имеет N₁ витков, а вторичная N₂ витков, то в обмотках индуцируются (без учета потерь на рассеивание магнитного потока) соответственно электродвижущие силы \(

\varepsilon_1 = — N_1\frac , \varepsilon_2 = — N_2\frac ,\) а их отношение \(

\frac = \frac , \) т.е. возникающие в катушках ЭДС индукции (самоиндукции) пропорциональны числу витков в них:

Отношение числа витков в первичной обмотке к числу витков во вторичной называют коэффициентом трансформации k .

Коэффициент трансформации определяется обычно при холостом ходе трансформатора, т.е. при разомкнутой цепи вторичной обмотки. В этом случае в первичной обмотке проходит так называемый ток холостого хода, действующее значение которого I_x. На основании закона Ома для замкнутой цепи действующие значения напряжения U₁, приложенного к первичной обмотке, ЭДС самоиндукции \(

\varepsilon_1\) и сила тока I_x в первичной обмотке связаны между собой соотношением \(

U_1 — \varepsilon_1 = I_x R_1,\) где R₁ — активное сопротивление первичной обмотки. Знак минус обусловлен тем, что ЭДС \(

\varepsilon_1\) согласно правилу Ленца противофазна U₁. Трансформатор проектируется так, чтобы в отсутствие нагрузки потребляемый из сети ток был незначительным. Это достигается выбором малого активного сопротивления R₁ и достаточно большого индуктивного сопротивления ωL. Для увеличения индуктивности катушки в нее вводят стальной сердечник и наматывают достаточно большое число витков N₁. Тогда сила тока \(

I_x \sim \frac 1\) будет мала и величиной I_x R₁ можно пренебречь. Следовательно, \(

U_1 \approx \varepsilon_1.\)

Цепь вторичной обмотки при холостом ходе разомкнута, вследствие чего в ней тока нет, и напряжение на зажимах вторичной обмотки равно индуцированной в ней ЭДС индукции \(

U_2 = \varepsilon_2.\) Поэтому коэффициент трансформации можно найти, измерив напряжения на концах катушек при холостом режиме

При включении во вторичную цепь какой-либо нагрузки (рабочий ход трансформатора) в ней начинает проходить ток нагрузки I₂ (переменный, такой же частоты). Ток I₂ создает в сердечнике магнитный поток, направленный по правилу Ленца навстречу потоку первичной обмотки. В результате суммарный поток магнитной индукции в первичной катушке уменьшается, уменьшается и ЭДС \(

\varepsilon_1,\) а следовательно, сила тока \(

I_1 = \frac \) увеличивается. Увеличение тока в первичной цепи приводит к увеличению магнитного потока, ЭДС индукции и силы тока во вторичной цепи. Но увеличение тока во вторичной цепи сопровождается увеличением тока самоиндукции и, следовательно, уменьшением магнитного потока (который только что возрастал). В конце концов при постоянной нагрузке устанавливаются определенные магнитный поток, ЭДС индукции во вторичной цепи, ток I₁ в первичной цепи (I₁ > I_x). Таким образом, увеличение тока I₂ во вторичной цепи автоматически приводит к увеличению тока I₁ в первичной цепи, т.е. трансформатор автоматически регулирует потребление энергии в зависимости от нагрузки во вторичной цепи.

При рабочем ходе трансформатора происходит непрерывная передача энергии из первичной цепи во вторичную. Мощность, потребляемая в первичной цепи \(

P_1 = I_1 U_1 \cos \varphi_1,\) а выделяемая на нагрузке \(

P_2 = I_2 U_2 \cos \varphi_2.\) Коэффициент полезного действия трансформатора

Не вся энергия, потребляемая от генератора, передается потребителю. При работе трансформатора имеются потери на нагревание обмоток трансформатора, на рассеивание магнитного потока в пространство, на вихревые токи Фуко (см. Закон электромагнитной индукции) в сердечнике и его перемагничивание. Для уменьшения этих потерь принимаются следующие меры: 1) обмотка низкого напряжения делается большего сечения, так как по ней проходит ток большей силы; 2) сердечник делают замкнутым, что уменьшает рассеивание магнитного потока; 3) сердечник делают из изолированных пластин для уменьшения токов Фуко и др. Благодаря этим мерам КПД современных трансформаторов достигает =95—99%, сдвиги фаз между колебаниями силы тока и напряжения близки к нулю \(

\left( \cos \varphi \approx 1\right).\)

Если иногда можно пренебречь потерями в трансформаторе, т.е. считать η =100%, то \(

P_1 = P_2 \Rightarrow I_1 U_1 = I_2 U_2 \Rightarrow \frac = \frac ,\) это значит, увеличивая с помощью трансформатора напряжение, мы во столько же раз уменьшаем силу тока и наоборот.

При рабочем режиме трансформатора напряжения на его обмотках уже не будут равны ЭДС. Учитывая потери только на активных сопротивлениях, напряжения U₁ и U₂ можно рассчитать, исходя из закона Ома для замкнутой цепи.

По закону Ома для замкнутой первичной цепи трансформатора алгебраическая сумма подводимого к трансформатору напряжения U₁ и возникающей ЭДС \(

\varepsilon_1\) самоиндукции равна падению напряжения в цепи (на активном сопротивлении первичной обмотки R₁):

U_1 — \varepsilon_1 = I_1 R_1\) Отсюда \(

U_1 = \varepsilon_1 + I_1 R_1.\)

Для подключенной нагрузки R роль источника тока выполняет вторичная обмотка, ЭДС в которой \(

\varepsilon_2.\) Она должна быть равна падению напряжения во вторичной цепи (на нагрузке R и на активном сопротивлении R₂ вторичной обмотки):

\varepsilon_2 = I_2 \left( R_2 + R\right), \) но \(

I_2 R = U_2.\) Следовательно, \(

\varepsilon_2 = U_2 + I_2 R_2.\) Откуда \(

U_2 = \varepsilon_2 — I_2 R_2. \)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 409-412.

www.physbook.ru

Трансформаторы. Передача электрической энергии

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы из магнитомягкого материала, на который намотаны две обмотки: первичная и вторичная (рис. 2.5.1).

Простейший трансформатор и его условное изображение в схемах. n₁ и n₂ – числа витков в обмотках

Первичная обмотка подсоединяется к источнику переменного тока с ЭДС e₁ (t), поэтому в ней возникает ток J₁ (t), создающий в сердечнике трансформатора переменный магнитный поток Φ, который практически без рассеивания циркулирует по замкнутому магнитному сердечнику и, следовательно, пронизывает все витки первичной и вторичной обмоток. В режиме холостого хода, то есть при разомкнутой цепи вторичной обмотки, ток в первичной обмотке весьма мал из-за большого индуктивного сопротивления обмотки. В этом режиме трансформатор потребляет небольшую мощность.

Ситуация резко изменяется, когда в цепь вторичной обмотки включается сопротивление нагрузки R_н, и в ней возникает переменный ток J₂ (t). Теперь полный магнитный поток Φ в сердечнике создается обоими токами. Но согласно правилу Ленца магнитный поток Φ₂, создаваемый индуцированным во вторичной обмотке током J₂, направлен навстречу потоку Φ₁, создаваемому током J₁ в первичной обмотке: Φ = Φ₁ – Φ₂. Отсюда следует, что токи J₁ и J₂ изменяются в противофазе, то есть имеют фазовый сдвиг, равный 180°.

Другой важный вывод состоит в том, что ток J₁ в первичной обмотке в режиме нагрузки значительно больше тока холостого хода. Это следует из того, что полный магнитный поток Φ в сердечнике в режиме нагрузки должен быть таким же, как и в режиме холостого хода, так как напряжение u₁ на первичной обмотке в обоих случаях одно и то же. Это напряжение равно ЭДС источника e₁ переменного тока. Так как магнитные потоки, пронизывающие обмотки, пропорциональны числу n₁ и n₂ витков в них, можно записать для первичной обмотки:

для вторичной обмотки:

Знак минус означает, что напряжения u₁ и u₂ находятся в противофазе, также как и токи J₁ и J₂ в обмотках. Поэтому фазовый сдвиг φ₁ между напряжением u₁ и током J₁ в первичной обмотке равен фазовому сдвигу φ₂ между напряжением u₂ и током J₂ во вторичной обмотке. Если нагрузкой вторичной обмотки является активное сопротивление R_н, то φ₁ = φ₂ = 0.

Для амплитудных значений напряжений на обмотках можно записать:

Коэффициент K = n₂ / n₁ есть коэффициент трансформации. При K > 1 трансформатор называется повышающим, при K

www.its-physics.org

Трансформаторы

1.1. Назначение и области применения

Трансформатором называют статическое электромагнитное устройство, имеющее две или большее число индуктивно-связанных обмоток и предназначенное для преобразования посредством электромагнитной индукции одной (первичной) системы переменного тока в другую (вторичную) систему переменного тока. Трансформаторы широко используются в промышленности и быту для различных целей.

1. Для передачи и распределения электрической энергии.

Обычно на электростанциях генераторы переменного тока вырабатывают электрическую энергию при напряжении 6-24 кВ, а передавать электроэнергию на дальние расстояния выгодно при значительно больших напряжениях (110, 220, 330, 400, 500, и 750 кВ). Поэтому на каждой электростанции устанавливают трансформаторы, осуществляющие повышение напряжения.

Распределение электрической энергии между промышленными предприятиями, населёнными пунктами, в городах и сельских местностях, а также внутри промышленных предприятий производится по воздушным и кабельным линиям, при напряжении 220, 110, 35, 20, 10 и 6 кВ. Следовательно, во всех распределительных узлах должны быть установлены трансформаторы, понижающие напряжение до величины 220, 380 и 660 В (рис. 1.1)

Рис. 1.1

2. Для обеспечения нужной схемы включения вентилей в преобразовательных устройствах и согласования напряжения на выходе и входе преобразователя. Трансформаторы, применяемые для этих целей, называются преобразовательными.

3. Для различных технологических целей: сварки (сварочные трансформаторы), питания электротермических установок (электропечные трансформаторы) и др.

4. Для питания различных цепей радиоаппаратуры, электронной аппаратуры, устройств связи и автоматики, электробытовых приборов, для разделения электрических цепей различных элементов указанных устройств, для согласования напряжения и пр.

5. Для включения электроизмерительных приборов и некоторых аппаратов (реле и др.) в электрические цепи высокого напряжения или же в цепи, по которым проходят большие токи, с целью расширения пределов измерения и обеспечения электробезопастности. Трансформаторы, применяемые для этих целей, называются измерительными.

Классификацию трансформаторов можно произвести по нескольким признакам:

1. По назначению трансформаторы разделяют на силовые общего и специального применения. Силовые трансформаторы общего применения используются в линиях передачи и распределения электроэнергии. Для режима их работы характерна частота переменного тока 50 Гц и очень малые отклонения первичного и вторичного напряжений от номинальных значений. К трансформаторам специального назначения относятся силовые специальные (печные, выпрямительные, сварочные, радиотрансформаторы), измерительные и испытательные трансформаторы, трансформаторы для преобразования числа фаз, формы кривой ЭДС, частоты и т.д.

2. По виду охлаждения – с воздушным (сухие трансформаторы) и масляным (масляные трансформаторы) охлаждением.

3. По числу фаз на первичной стороне – однофазные и трёхфазные.

4. По форме магнитопровода – стержневые, броневые, тороидальные.

5. По числу обмоток на фазу – двухобмоточные, трёхобмоточные, многообмоточные (более трёх обмоток).

6. По конструкции обмоток – с концентрическими и чередующимися (дисковыми) обмотками.

1.2. Принцип действия трансформатора

Электромагнитная схема однофазного двухобмоточного трансформатора состоит из двух обмоток (рис. 1.2), размещенных на замкнутом магнитопроводе, который выполнен из ферромагнитного материала. Применение ферромагнитного магнитопровода позволяет усилить электромагнитную связь между обмотками, т.е. уменьшить магнитное сопротивление контура, по которому проходит магнитный поток трансформатора. Первичную обмотку 1 подключают к источнику переменного тока – электрической сети с напряжением сети u₁. К вторичной обмотке 2 присоединяют сопротивление нагрузки Zн.

Обмотку более высокого напряжения называют обмоткой высшего напряжения (ВН), а низкого напряжения – обмоткой низшего напряжения (НН). Начала и концы обмотки ВН обозначают буквами А и Х; обмотки НН – буквами а и х.

При подключении к сети в первичной обмотке возникает переменный ток i₁, который создаёт переменный магнитный поток Ф, замыкающийся по магнитопроводу. Поток Ф индуцирует в обеих обмотках переменные ЭДС – е₁ и е₂ пропорциональные, согласно закону Максвелла, числам витков w₁ и w₂ соответствующей обмотки и скорости изменения потока dФ/dt.

Рис. 1.2

Таким образом, мгновенные значения ЭДС, индуцированные в каждой обмотке.

Следовательно, отношение мгновенных и действующих ЭДС в обмотках определяется выражением

Если пренебречь падениями напряжения в обмотках трансформатора, которые обычно не превышают 3-5 % от номинальных значений U₁ и U₂, и считать E₁≈U₁ и E₂≈U₂, то получим

Следовательно, подбирая соответствующим образом числа витков обмоток, при заданном напряжении U₁ можно получить желаемое напряжение U₂. Если необходимо повысить вторичное напряжение, то число витков w₂ берут больше числа w₁; такой трансформатор называют повышающим. Если требуется уменьшить напряжение U₂, то число витков w₂ берут меньшим w₁; такой трансформатор называют понижающим.

Отношение ЭДС E_вн обмотки высшего напряжения к ЭДС Е_нн обмотки низшего напряжения (или отношение их чисел витков) называют коэффициентом трансформации

.

Коэффициент n всегда больше единицы.

В системах передачи и распределения энергии в ряде случаев применяют трёхобмоточные трансформаторы, а в устройствах радиоэлектроники и автоматики – многообмоточные трансформаторы. В таких трансформаторах на магнитопроводе размещают три или большее число изолированных друг от друга обмоток, что даёт возможность при питании одной из обмоток получать два или большее число различных напряжений (U₂, U₃, U₄ и т.д.) для электроснабжения двух или большего числа групп потребителей. В трехобмоточных силовых трансформаторах различают обмотки высшего, низшего и среднего (СН) напряжения.

В трансформаторе преобразуются только напряжения и токи. Мощность же остаётся приблизительно постоянной (она несколько уменьшается из-за внутренних потерь энергии в трансформаторе). Следовательно, полная мощность потребляемая из сети

практически полностью выделяется на нагрузке

Отсюда следуют соотношения между токами и напряжениями на первичной и вторичной обмотках трансформатора.

При уменьшении вторичного напряжения в n раз по сравнению с первичным, ток i₂ во вторичной обмотке соответственно увеличится в n раз.

Трансформатор может работать только в цепях переменного тока. Если первичную обмотку трансформатора подключить к источнику постоянного тока, то в его магнитопроводе образуется магнитный поток, постоянный во времени по величине и направлению. Поэтому в первичной и вторичной обмотках в установившемся режиме не индуцируются ЭДС, а, следовательно, не передаётся электрическая энергия из первичной цепи во вторичную. Такой режим опасен для трансформатора, так как из-за отсутствия ЭДС E₁ в первичной обмотке ток I₁ = U₁ / R₁ весьма большой.

Важным свойством трансформатора, используемым в устройствах автоматики и радиоэлектроники, является способность его преобразовывать сопротивление нагрузки. Если к источнику переменного тока подключить нагрузку с сопротивлением R через трансформатор с коэффициентом трансформации n, то для цепи источника

,

где: Р₁ – мощность, потребляемая трансформатором от источника переменного тока, Вт;
– мощность, потребляемая нагрузкой с сопротивлением R от трансформатора.

Таким образом, трансформатор изменяет значение сопротивления нагрузки R в n 2 раз. Это свойство широко используется при разработке электрических схем для согласования сопротивлений нагрузки с внутренним сопротивлением источников электрической энергии.

1.3. Устройство трансформаторов

Магнитная система. В зависимости от конфигурации магнитной системы, трансформаторы подразделяют на стержневые (рис. 1.3, а), броневые (рис.1.3, б) и тороидальные (рис. 1.3, в).

Стержнем называют часть магнитопровода, на которой размещают обмотки (рис. 1.3; 2). Часть магнитопровода, на которой обмотки отсутствуют, называют ярмом (рис. 1.3; 1). Трансформаторы большой и средней мощности обычно выполняют стержневыми. Они имеют лучшие условия охлаждения и меньшую массу, чем броневые.

Рис. 1.3

Для уменьшения потерь от вихревых токов, магнитопроводы трансформаторов (рис. 1.3) собирают из изолированных листов электротехнической стали толщиной 0,28-0,5 мм при частоте 50 Гц.

Трансформаторы малой мощности и микротрансформаторы часто выполняют броневыми, так как они имеют более низкую стоимость по сравнению со стержневыми трансформаторами из-за меньшего числа катушек и упрощения сборки и изготовления. Применяют также и маломощные трансформаторы стержневого типа с одной или двумя катушками (рис. 1.3; 3). Преимущество тороидальных трансформаторов – отсутствие в магнитной системе (рис. 1.3; 4) воздушных зазоров, что значительно уменьшает магнитное сопротивление магнитопровода. В трансформаторах малой мощности магнитопровод собирают из штамповых пластин П-, Ш- и О- образной формы (рис. 1.4, а, б, в).

Широкое применение получили магнитопроводы, навитые из узкой ленты электротехнической стали или из специальных железоникелевых сплавов типа пермаллой. Их можно использовать для стержневых, броневых, тороидальных и трёхфазных трансформаторов (рис 1.4 г, д, е, ж).

Рис. 1.4

Монолитность конструкции ленточного магнитопровода обеспечивается путём применения клеющих лаков и эмалей.

Для трансформаторов, работающих при частоте 400 и 500 Гц, магнитопроводы выполняют из специальных сортов электротехнической стали с малыми удельными потерями при повышенной частоте, а также из железоникелевых сплавов типа пермаллой, которые имеют большие начальную и максимальную магнитные проницаемости и позволяют получить магнитные поля с большой индукцией при сравнительно слабой напряжённости. Толщина листов составляет 0.2; 0,15; 0.1 и 0.08 мм. При частотах более10-20 кГц магнитопроводы прессуют из порошковых материалов (магнитодиэлектриков и ферритов).

Обмотки. В современных трансформаторах первичную (рис. 1.5; 1) и вторичную (рис. 1.5; 3, 4, 5) обмотки стремятся расположить для лучшей магнитной связи как можно ближе одну к другой. При этом на каждом стержне магнитопровода (рис. 1.5; 2) размещают обе обмотки либо концентрически – одну поверх другой (рис. 1.5 а), либо в виде нескольких дисковых катушек, чередующиеся по высоте стержня (рис. 1.5 б). В первом случае обмотки называют концентрическими, во втором – чередующимися. В силовых трансформаторах обычно применяют концентрические обмотки, причём ближе к стержням располагают обмотку НН, требующей меньшей изоляции относительно остова трансформатора, а снаружи – обмотку ВН.

В трансформаторах малой мощности и микротрансформаторах используют однослойные и многослойные обмотки из круглого провода с эмалевой или хлопчатобумажной изоляцией, которые наматывают на гильзу или на каркас из электрокартона (рис. 1.5; а); между слоями проводов прокладывают изоляцию из кабельной бумаги или ткани.

Рис. 1.5

В микротрансформаторах часто выполняют из алюминиевой фольги толщиной 30-20 мкм. Изоляцией здесь служит окисная плёнка фольги, которая обладает достаточной теплоёмкостью, теплопроводностью и может выдерживать рабочее напряжение до 100 В.

1.4. Идеализированный трансформатор

Для выяснения сущности физических процессов, происходящих в трансформаторе, рассмотрим идеализированный трансформатор, у которого магнитный поток Ф полностью замыкается по стальному магнитопроводу и сцеплен с обеими обмотками, а потери в стали отсутствуют. К первичной обмотке трансформатора (рис. 1.6, а) подводится синусоидальное напряжение , благодаря чему по этой обмотке проходит переменный ток, создающий переменный магнитный поток. Переменный поток наводит в обмотках трансформатора ЭДС

; .

В режиме холостого хода цепь вторичной обмотки разомкнута и ток i₂=0. При этом для контура первичной обмотки трансформатора

,

где: u₁ – мгновенное значение приложенного к первичной обмотке напряжения.

Уравнение (1.6) справедливо, если принять, что не только i₂=0, но и отсутствуют потери в стали магнитопровода (от вихревых токов и гистерезиса); иначе эти потери должны были бы учитываться в виде потерь от тока, проходящего по замкнутой накоротко вторичной обмотке с большим активны сопротивлением.

Вводя в формулу (1.6) значение ЭДС , индуцируемой в первичной обмотке переменным магнитным потоком, и пренебрегая падением напряжения в активном сопротивлении первичной обмотки i₁R₁ из-за его малости, получаем

т.е. напряжение, приложенной к первичной обмотке, практически полностью уравновешивается индуцированной в этой обмотке ЭДС.

Рис. 1.6

Если питающее напряжение u₁ – изменяется по синусоидальному закону , то магнитный поток также изменяется синусоидально, отставая по фазе от приложенного напряжения на угол 90°,

.

Можно показать, что постоянная интегрирования в установившемся режиме С=0.

Связь между ЭДС и магнитным потоком определяется из уравнения

,

и выражается для амплитудного значения ЭДС формулой или для действующего значения формулой

.

Учитывая синусоидальный характер изменения напряжения u₁ и ЭДС e₁, уравнение (1.7) можно представить в комплексной форме:

.

Уравнение (1.9) справедливо для идеализированного трансформатора, в котором пренебрежимо мало активное сопротивление обмоток и отсутствуют потери в стали магнитопровода. Однако, несмотря на принятые допущения, оно правильно определяет сущность качественных процессов, происходящих в трансформаторе, и поэтому является одним из фундаментальных в теории электрических машин. Количественные ошибки, вызванные идеализацией трансформатора, можно всегда довольно легко подсчитать.

Предположив, что насыщение в стали трансформатора отсутствует и весь магнитный поток замыкается по стальному магнитопроводу, можно считать ток первичной обмотки идеализированного трансформатора прямо пропорциональным магнитному потоку. В связи с этим, на векторной диаграмме идеализированного трансформатора в режиме холостого хода (рис 1.6 ,б) ток холостого хода Í₁₀ изображён вектором, совпадающий по направлению с вектором магнитного потока. . На этой же диаграмме векторы ЭДС É₁ и напряжения Ú₁ показаны в противофазе в соответствии с уравнением (1.9), а вектор магнитного потока опережает вектор ЭДС на 90°. Поскольку магнитный поток не имеет действующего значения, на диаграмме показано его амплитудное значение. Там же показан вектор ЭДС É₂ совпадающий по фазе с вектором É₁, так как ЭДС É₂ индуцируется тем же самым магнитным потоком, что и É₁, и может быть определена по формуле

.

При работе под нагрузкой для первичной обмотки идеализированного трансформатора можно написать уравнение

,

где: Ф₁ и Ф₂ – потоки, создаваемые токами первичной и вторичной обмоток.

Обозначая, как и при холостом ходе, , получаем

т.е. такое же соотношение, что и при холостом ходе. Очевидно, если первичное напряжение при нагрузке идеализированного трансформатора остаётся неизменным, то величина ЭДС е₁ такая же, как и при холостом ходе. Следовательно, результирующий поток при нагрузке равен потоку при холостом ходе:

или в комплексной форме

.

Неизменность магнитного потока при переходе от режима холостого хода к режиму нагрузки является важнейшем свойством трансформатора. Из этого свойства следует закон равновесия магнитодвижущих сил (МДС) в трансформаторе:

,

где: F₁ и F₂ – МДС, создаваемые первичной и вторичной обмотками трансформатора при нагрузке;
F₁₀ – МДС, создаваемая первичной обмоткой при холостом ходе.

При переменном токе оперируют с амплитудами МДС; при этом из (1.12) следует, что

.

Для наглядности уравнение (1.13) можно представить иначе:

,

где: — нагрузочная составляющая тока первичной обмотки (приведенный ток нагрузки).

Таким образом, МДС, создаваемая током I’₂ равна по величине и противоположна по фазе МДС вторичной обмотки, т.е. компенсирует МДС вторичной обмотки. Это обуславливает неизменность магнитного потока трансформатора. Векторная диаграмма идеализированного трансформатора, работающего с нагрузкой, показана на (рис. 1.6, в). Мощность нагрузочной составляющей первичного тока равна мощности, отдаваемой трансформатором нагрузке, так как

.

Следовательно, нагрузочная составляющая тока I₁ не только уравновешивает МДС вторичной обмотками, но и обеспечивает поступление в трансформатор из сети мощности, отдаваемой приёмнику электрической энергии, подключённому к вторичной обмотке.

Основные закономерности работы идеализированного трансформатора справедливы и для реальных трансформаторов.

1.5. Намагничивающий ток и ток холостого хода

Намагничивающий ток. Величина и форма тока холостого хода определяются магнитным потоком трансформатора и свойствами его магнитной системы. Выше показано, что магнитный поток изменяется во времени синусоидально: , а его амплитуда определяется ЭДС:

.

Так как при холостом ходе ЭДС практически равна напряжению, то значение магнитного потока определяется напряжением первичной обмотки, её числом витков и частотой.

Свойства магнитной системы трансформатора описываются в основном магнитной характеристикой, представляющей собой графическое изображение зависимости магнитного потока Ф от МДС трансформатора F или намагничивающего тока I_η, пропорционального МДС.

Активная составляющая тока холостого хода. Намагничивающий ток I_η является главной составляющей тока холостого хода трансформатора I₁₀. Этот ток является реактивным, т.е. I_η=I_10p. Однако реальный трансформатор в режиме холостого хода потребляет от источника переменного тока некоторую активную мощность, так как при переменном магнитном потоке в стальном магнитопроводе возникают потери энергии от гистерезиса и вихревых токов (магнитные потери ΔP_c). Поэтому ток холостого хода I₁₀ должен иметь еще и активную составляющую , которая обеспечивает поступление в первичную обмотку мощности, компенсирующей магнитные потери (электрическими потерями в первичной обмотке в этом режиме можно пренебречь из-за малости тока холостого ход). Следовательно, ток холостого хода

или .

Обычно при выполнении магнитопровода трансформатора из листовой электротехнической стали толщиной 0,28-0,50 мм и частоте 50 Гц активная составляющая тока I_10a не превышает 10% от тока I₁₀, поэтому она оказывает весьма малое влияние на значение ток холостого хода (изменяет его не более чем на 1%). Форма кривой тока холостого хода определяется в основном кривой намагничивающего тока.

1.6. Комплексные уравнения и векторная диаграмма реального трансформатора

В реальном трансформаторе помимо основного магнитного потока Ф, замыкающегося по магнитопроводу и сцепленного со всеми обмотками трансформатора, имеются также потоки рассеяния Ф_σ1 и Ф_σ2 (рис 1.7), которые сцеплены только с одной из обмоток. Потоки рассеяния не участвуют в передаче энергии, но создают в каждой из обмоток соответствующие ЭДС самоиндукции ; .

Рис. 1.7

C учетом ЭДС самоиндукции и падений напряжения в активных сопротивлениях обмоток можно составить комплексные уравнения для первичной и вторичной обмоток трансформатора. С учетом (1.13) получим следующую систему уравнений:

где: — сопротивление нагрузки, подключенной к трансформатору.

Поскольку потоки рассеяния полностью или частично замыкаются по воздуху, они пропорциональны МДС соответствующих обмоток или соответствующим токам:

; .

Величины X1 и X2 называют индуктивными сопротивлениями обмоток транс-форматора, обусловленными потоками рассеяния. Так как векторы ЭДС Е_σ1 и Е_σ2отстают от соответствующих потоков и токов на 90°, то

; .

При этом комплексные уравнения трансформатора примут вид

;

;

.

Замена ЭДС и падениями напряжений j Í₁ X₁ и j Í₁ X₂ наглядно показывает роль потоков рассеяния: они создают индуктивные падения напряжения в обмотках, не участвуя в передаче энергии из одной обмотки в другую. Проще становится и построение векторной диаграммы, соответствующей системе уравнений (1.20) – (1.22), в которой целесообразно также заменить падение напряжения в нагрузке величиной , т.е. вторичным напряжением трансформатора, определяемым из (1.21):

.

Векторную диаграмму вторичной обмотки трансформатора (рис. 1.8, а) строят согласно уравнению (1.23). Характер диаграммы определяется током нагрузки Í₂, который принимается заданным по величине и фазе. Иными словами, задаваясь векторами вторичного тока Í₂ и напряжения Ú₂, можно построить вектор ЭДС

,

если известны параметры трансформатора. Вектор Í₂ R₂ параллелен вектору тока Í₂, a вектор j Í₂ X₂ опережает вектор тока Í₂ на угол 90°. На диаграмме изображен и вектор магнитного потока , который опережает вектор ЭДС É₂ на 90°. Векторную диаграмму первичной обмотки трансформатора (рис. 1.8, б) строят в соответствии с уравнением

.

Построение диаграммы начинают с вектора потока , который создается током холостого хода Í₁₀. Этот ток опережает вектор потока на угол . Вектор ЭДС É₁, как и É₂, отстает от потока на угол 90°.

Рис. 1.8

Ток в первичной обмотке трансформатора , поэтому на рис.1.8,б нужно показать и вектор тока Í₂, сдвинутый на угол ψ₂ относительно вектора É₁ (векторы É₁ и É₂ совпадают по направлению). Зная Í₂, можно изобразить вектор и получить вектор Í₁ как сумму векторов Í₁₀ и .

Найдя вектор тока Í₁, можно определить значения векторов Í₁ R₁ и j Í₁ X₁ и построить искомый вектор напряжения Ú₁ как сумму трех составляющих: векторов -É₁ и падений напряжений в обмотках Í₁ R₁ и j Í₁ X₁.

1.7. Схема замещения трансформатора

Составление схемы замещения. Систему уравнений (1.20) – (1.22), описывающую электромагнитные процессы в трансформаторе, можно свести к одному уравнению, если учесть, что , и положить

.

При этом параметры R₀ и X₀ следует выбирать так, чтобы в режиме холостого хода, когда ЭДС E₁ практически равна номинальному напряжению U₁, ток

по модулю равнялся бы действующему значению тока холостого хода, а мощность – мощности, забираемой трансформатором из сети при холостом ходе.

Решим систему уравнений (1.20) – (1.22) относительно первичного тока

.

В соответствии с уравнением (1.28) трансформатор можно заменить электрической схемой, по которой можно определить токи Í₁ и Í₂, мощность P₁, забираемую из сети, мощность ΔP потерь и т.д. Такую электрическую схему называют схемой замещения трансформатора (рис.1.9).

Рис. 1.9

Эквивалентное сопротивление этой схемы

,

где: ;
;
;
.

Схема замещения трансформатора представляет собой сочетание двух схем замещения — первичной и вторичной обмоток, которые соединены между собой в точках а и б. В цепи первичной обмотки включены сопротивления R₁ и X₁, а в цепи вторичной обмотки – сопротивления R′₂ и X′₂. Участок схемы замещения между точками а и б, по которому проходит ток I₁₀, называют намагничивающим контуром. На вход схемы замещения подают напряжение Ú₁, к выходу ее подключают переменное сопротивление нагрузки , к которому приложено напряжение –Ú′₂.

Сопротивления (и его составляющие R′₂ = R₂ n 2 и X′₂ = X₂n 2 ), а также называют соответственно сопротивлениями вторичной обмотки и нагрузки, приведенными к первичной обмотке. Аналогично приведенными называют значения ЭДС и тока : E′₂ = nE₂ ; .

Полная мощность приведенного контура вторичной обмотки в схеме замещения равна мощности вторичной обмотки реального трансформатора: I′₂ E′₂= (I₂ /n )E₂n = E₂ I₂, а мощность электрических потерь в приведенном вторичном контуре этой схемы равна мощности потерь во вторичной обмотке реального трансформатора: .

Относительные падения напряжений в активном и индуктивном сопротивлениях приведенного вторичного контура также остаются неизменными, как и в реальном трансформаторе:

;
.

1.8. Определение параметров схемы замещения

Параметры схемы замещения для любого трансформатора можно определить по данным опытов холостого хода (рис. 1.10) и короткого замыкания (рис. 1.12).

Опыт холостого хода

В опыте холостого хода (рис. 1.10) вторичная обмотка трансформатора разомкнута, а к первичной подводится номинальное напряжение U_1н = U₁₀.

Рис. 1.10

Схема замещения трансформатора (рис. 1.9) для режима холостого хода (I₂=0) примет вид (рис. 1.11).

Рис. 1.11

Измерив ток холостого хода I₁₀ и мощность P₁₀, потребляемую трансформатором, согласно схеме замещения (рис. 1.11,а) находим

где: Z_{вх х} – входное сопротивление трансформатора при опыте холостого хода.

Так как ток холостого хода мал по сравнению с номинальным током трансформатора, электрическими потерями ΔP_эл1 = I 2 ₁₀ R₁ пренебрегают и считают, что вся мощность, потребляемая трансформатором, расходуется на компенсацию магнитных потерь в стали магнитопровода. При этом

,

Аналогично считают, что X₁ + X₀ ≈ X₀, так как сопротивление X₀ определяется основным потоком трансформатора Ф (потоком взаимоиндукции), а X₁ – потоком рассеяния Ф_Δ1, который во много раз меньше Ф. Поэтому с большой степенью точности полагают, что

Z₀ = U₁₀ / I₁₀ ; .

Измерив напряжения U₁₀ и U₂₀ первичной и вторичной обмоток, определяют коэффициент трансформации

Векторная диаграмма трансформатора в режиме холостого хода, построенная исходя из указанных выше допущений, изображена на рис. 1.11, б. В действительности ток Í₁₀ создает в первичной обмотке падения напряжения Í₁₀ R₁ и j Í₁₀ X₁, поэтому . Соответствующая векторная диаграмма показана на рис. 1.11, в.

Опыт короткого замыкания

Вторичную обмотку замыкают накоротко сопротивление Z_н = 0), а к первичной подводят пониженное напряжение (см. рис.1.12) такого значения, при котором по обмоткам проходит номинальный ток I_ном. В мощных силовых трансформаторах напряжение U_к при коротком замыкании обычно составляет 5-15% от номинального. В трансформаторах малой мощности напряжение U_к может достигать 25-50% от U_ном.

Рис. 1.12

Так как поток, замыкающийся по стальному магнитопроводу, зависит от напряжения приложенного к первичной обмотке трансформатора, а магнитные потери в стали пропорциональны квадрату индукции, т.е. квадрату магнитного потока, то ввиду малости U_к пренебрегают магнитными потерями в стали и током холостого хода. При этом из общей схемы замещения трансформатора исключают сопротивления R₀ и X₀ и преобразуют ее в схему, показанную на (рис 1.13, а). Параметры этой схемы определяют из следующих соотношений:

model.exponenta.ru