Справочник химика 21

Химия и химическая технология

Гаусса закон распределения

Результаты определения дисперсного состава пыли обычно представляют в виде зависимости массовых (иногда счетных) фракций частиц от их размера. Под фракцией понимают массовые (счетные) доли частиц, содержащиеся в определенном] интервале размеров частиц. Распределение частиц примесей по размерам может быть различным, однако на практике оно часто согласуется с логарифмическим нормальным законом распределения Гаусса (ЛНР). В интегральной форме это распределение описывают формулой [c.283]

Эти довольно естественные предположения и приводят к так называемому нормальному закону распределения вероятностей, выраженному формулой и кривыми Гаусса, Математическое выражение закона Гаусса — уравнение гауссовой кривой — имеет вид [c.25]

В теории надежности механических систем наиболее часто используют следующие законы распределения нормальный (Гаусса), экспоненциальный и Вейбулла. Эти три закола хорошо согласуются с различными видами поведения случайных величин, характеризующих приработочные и внезапные отказы машин и отказы вследствие износа (старение узлов, деталей). Законы распределения и формулы теории надежности приведены в табл. 12.1. [c.521]

Пример гауссов закон распределения. Рассмотрим гауссовы случайные величины, характеризующиеся средними значениями ( а) и корреляторами S ,p — [c.461]

Коэффициенты (1 — р ) приведены в последней строке табл. 2. Из табл. 2 видно, что если положить ро = 0,95, то для произвольного закона распределения с известной дисперсией доверительный интервал не превышает 5а (напомним, что для распределения Гаусса он равен 2а . Если вместо использовать найденное по тем же измерениям значение 5 , то нужно строить критерий типа Стьюдента. Оценки при этом, однако, будут существенно хуже приведенных. Если такая точность недостаточна, то необходимо либо проверить имеющиеся данные на нормальность распределения, либо оценить возможную опшбку для двух крайних случаев распределения. [c.145]

Закон распределения по скоростям близок по форме к найденному Гауссом закону распределения ошибок наблюдений, играющему важную роль при точных измерениях (астрономия, геодезия, физика) и в статистике. [c.152]

Нормальный закон распределения. Производственные погрешности при наличии многих независимых и равноценных по величине случайных причин (например, при автоматическом получении размеров) во многих случаях подчиняются нормальному закону распределения (закону Гаусса). Теоретическая кривая (фиг. 5) этого закона определяется уравнением [c.17]

На основании экспериментальных исследований (гл. П), выявлено, что распределения отклонений размеров деталей описанных сопряжений, а следовательно, и зазоров между ними, следуют закону Гаусса (закону нормального распределения). [c.141]

Практически в большинстве физических измерений отклонения от х тем реже (менее вероятны), чем больше они по величине кроме того, эти отклонения в обе стороны в равной степени вероятны. При этом выполняется нормальный закон распределения ошибок, аналитический вид которого предложен Гауссом. Зависимость р (у) для нормального распределения показана на рис. И-1. [c.37]

Как правило, при большом числе изделий в партии больше вероятность того, что рассеяние значений выходного показателя будет подчиняться нормальному закону распределения (закону Гаусса). В этом случае если поле рассеяния сй ограничить величиной, равной 6а, то число значений выходного показателя, вышедших за пределы 6а, составит 0,27%. [c.31]

Гауссом был найден закон распределения случайных ошибок. Этот закон справедлив почти для любых измерений, в том числе и для количественного спектрального анализа. На рис. 135, а графически показана зависимость числа измерений, в которых встречается та или иная ошибка, от ее величины при достаточно большом числе измерений. [c.226]

В теории ощибок доказывается, что при условии выполнения нормального закона (закона распределения Гаусса) при п измерениях одинаковой точности среднее арифметическое из результатов, полученных при всех измерениях, является наиболее вероятным и наилучшим значением измеряемой величины [c.27]

Выражение (IV. 19) называют нормальным законом распределения (рис. IV. 14), оно введено впервые Гауссом при анализе теории ошибок. Условие нормировки выполняется [c.140]

График уравнения (III. 12) показан на рис. 24. Он аналогичен кривой закона распределения ошибок Гаусса. [c.50]

Нормальный закон распределения случайных ошибок. Случайные ошибки измерения характеризуются определенным законом их распределения. К наиболее простым и достаточно точно отражающим действительность, относится нормальный закон распределения, или закон Гаусса [c.313]

Теперь необходимо выяснить важный практический вопрос какое же наименьшее количество измерений нужно сделать, чтобы достаточно надежно характеризовать данную методику. Если число измерений мало, то среди них может оказаться слишком много или наоборот слишком мало результатов с большой ошибкой, чем ЭТО следует из закона распределения. Поэтому, прежде чем подсчитывать ошибку, которую дает данная методика, необходимо убедиться, что хотя бы примерно выполняется закон распределения Гаусса. В этом случае [c.229]

Распределения, удовлетворяющие соотнощению (3.14) и сводимые к нему путем простых преобразований, называют нормальными, а закон распределения — нормальным законом распределения случайных величин Гаусса. Распределение Гаусса называется нормальным в силу того, что многие распределения, отражающие самые разнообразные явления случайного характера, протекающие в природе, подчиняются этому закону. [c.78]

Установлено, что изменение равновесного выхода в данном случае может быть описано с помощью нормального закона распределения Гаусса [c.10]

Б. Может, однако, случиться так, что (3.42) не будет выполняться, т. е. гипотеза о нормальном распределении не подтверждается. Тогда следует оценить параметры, определить дисперсии и доверительные интервалы для двух каких-либо наиболее резко различающихся распределений. Обычно выбирают нормальное (Гаусса) и двойное экспоненциальное (Лапласово) распределения. Сравнение дисперсий для обоих видов распределения объективно дает оценку максимально возможных опшбок измерения, обусловленных незнанием закона распределения. [c.146]

Величина или А при распределении отклонений размеров отверстия и вала по нормальному закону распределения (закону Гаусса) будет несколько больше, чем рассчитанные по формуле (126), так как центр группирования отклонений зазора будет совпадать с величиной среднего зазора. Однако стремление рабочего к зоне исправимого брака изменяет закон нормального-распределения, увеличивая количество отклонений, попадающих в зону Ар, а следовательно, и процент риска. Для учета изменения асимметрии нормального закона распределения начало кривой распределения перенесено к границе минимального допустимого зазора Amin (фиг. 51). [c.143]

На основание опытных данных было предположено, что вероятность образования Р,(х,) и разложения Pj(x) i-ro компонента системы подчиняется нормальному закону распределения Гаусса. Тогда событие неразложения i-ro компонента системы является противоположным событию его разложения и его вероятность определяется как [c.231]

Вероятность событий, способствующих существованию в системе i -го компонента, подчиняется нормальному закону распределения Гаусса. Совокупность таких событий оценивали, так называемым, кинетическим фактором Kj=lnkr. К/ — обобщенный кинетический фактор, характеризуюшлй условия проведения пиролиза. Он близок по смыслу известному фактору жесткости пиролиза / который зависит от температуры Т и времени контакта г. Предлагаемый нами фактор зависит и от кажущейся энергии активации разложения углеводорода, что важно при термокаталитическом пиролизе. [c.154]

В теории погрешностей доказывается, что если погрешности следуют закону распределения Гаусса, то наиболее вероятным и надежным значением измеряемой величины является математическое ожидание или среднее арифметическое полученных равноточных результатов измерений. Строго это положение относится к гипотетической генеральной совокупности, т. е. совокупности всех наблюдений, мыслимых при данных условиях. Арифметическое среднее этих наблюдений называют генеральным средним ц. В аналитической химии число параллельных определений обычно невелико и совокупность полученных результатов называют выборочной совокупностью или случайной выборкой. Сред-нее значение результатов случайной выборки называют в ы-борочным средним. Методами статистического анализа можно по результатам случайной выборки оценить параметры генеральной совокупности и таким образом найти наиболее вероятное значение содержания компонента в пробе. [c.126]

Случайные отклонения при малом числе опытов. На практике экспериментатор выполняет не бесконечно большое число опытов, а довольно малое (2—10), и имеет дело не с генеральной, а с выборочной совокупностью вариант (см. табл. 7.3). При этом распределение случайных ошибок подчиняется уже не закону Гаусса, а /-распределению, имеющему ту же форму, что и кривая Гаусса, но с большей величиной а. При этом /-критерий (или иначе ко- эффициент Стьюдента — Фише- «щ ра) зависит от доверительной е вероятности (Р) и числа опытов минус 1 (р = п.—1). Последнее представляет собой число степе- ней свободы и вводится тогда, когда неизвестно истинное значе- ние, а рассчитывается среднее X, поэтому при расчете дисперсии выборочной совокупности (5 ) в знаменателе ставится л—1. [c.135]

Численные данные, получаемые при выполненин нескольких параллельных аналитических определений, обычно незначительно, но все же отличаются друг от друга. Эти отличия вызываются случайными причинами, и они обнаруживаются даже при самой тщательной работе химика-аналитика. Выяснить и устранить причины случайных отклонений невозможно. Нельзя также заранее предсказать, чему будет равно случайное отклонение каждого результата следующих определений. (Эднако при выполнении большого числа определений проявляется зависимость частоты появления отклонения от его величины. Обычно частота появления отклонения при этом подчиняется нормальному закону распределения (распределению Гаусса). Лишь в случае таких методов анализа, когда измерения ведутся подсчетом импульсов (в радиохимии), подсчетом квантов (в рентгеноспектральном анализе) и т. п., она подчиняется другому закону распределения, называемому распределением Пуассона. [c.132]

Предположим, что в единичной компактной струе секундное количество примеси, проходящее через поперечное сечение струи сохраняется постоянным (примесь химически стойкая и не сорбируется подстилающей поверхностью), а распределение концентрации примеси совпадает с лормальным законом распределения Гаусса. [c.103]

Если бы для воздушной сепарации как-одного из процессов разделения была известна математическая функция, описывающая к. п. в., эффективность сепарации однозначно определялась бы значениями параметров этой функции. Однака обоснованное математическое описание пока отсутствует. Движение массы разных- частиц в воздушном сепараторе подчиняется некоторому физико-статистиче-скому закону. Имеется много попыток заменить его чисто статистическим законом,, например законом нормального распределения ошибок Гаусса, законом нормально-логарифмического раопределення и т. д. При -этом сходство реальной к. п. в. с кривой, соответствующей формальному математическому описанию, является чисто внешним и не дает никакой новой информации о процессах, протекающих при сепарации. Об этом, в частности, свидетельствует тот факт, что в ряде случаев к. п. в. лучше аппроксимируется такими не имеющими прямого отттошения к статистике функциями, как неполная гамма-функция, гиперболический тангенс и др. [Л. 39]. [c.58]

Фактор жесткости определяет вероятность событий, способствующих существованию в системе /-го компонента, подчиняемую нормальному закону распределения Гаусса. Используя нормальную функцию распределения и основные законы теории вероятности, получили уравнения для расчета выхода компонентов в продуктах пиролиза. Вероятности образования и разложения /-го компонента системы р1( ) и р2( ) описывались нормальной функцией распределения. Вероятность неразложения /-го компонента системы является противоположной вероятности его разложения и определяется по формуле [c.15]

Размер гибкой цепи (степень свернутости) оценивают расстоянием между ее концами h (см. рис. 5.2, в). Оно варьируется в широком интервале. Предельные значения = О и = L (где L — длина предельно вы тя-нутой зигзагообразной цепи с недеформированными валентными углами) маловероятны. Число возможных конформаций И для данного расстояния h и распределение макромолекул по расстояниям между концами подчиняются закону распределения Гаусса (рис. 5.3). Наиболее вероятно расстояние, соответствующее максимуму кривой распределения. [c.123]

Смотреть страницы где упоминается термин Гаусса закон распределения: [c.57] [c.94] [c.19] [c.18] [c.60] [c.65] [c.112] [c.243] Аналитическая химия Часть 1 (1989) — [ c.127 ]

chem21.info

Распределение Гаусса

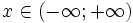
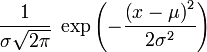
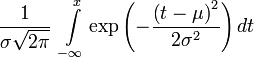
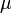
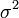
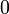
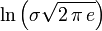
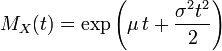
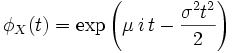
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Содержание

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Статистическая проверка принадлежности нормальному распределению

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:

• Критерий Пирсона
• Критерий Колмогорова-Смирнова
• Критерий Андерсона-Дарлинга (англ.)
• Критерий Жака-Бера (англ.)
• Критерий Шапиро-Вилка (англ.)
• «График нормальности» (англ.) — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.

Заключение

Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:

• отклонение при стрельбе
• ошибки при измерениях
• рост человека

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.

Wikimedia Foundation . 2010 .

Смотреть что такое «Распределение Гаусса» в других словарях:

РАСПРЕДЕЛЕНИЕ ГАУССА — син. термина распределение нормальное. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

распределение Гаусса — Gauso skirstinys statusas T sritis fizika atitikmenys: angl. Gauss distribution; gaussian distribution; Laplace Gauss distribution vok. Gauß Verteilung, f rus. Гауссово распределение, n; распределение Гаусса, n pranc. distribution de Gauss, f;… … Fizikos terminų žodynas

РАСПРЕДЕЛЕНИЕ ГАУССА — (Gaussian distribution) см. Частота распределения, значимость … Толковый словарь по медицине

Распределение Гаусса (Gaussian Distribution) — см. Частота распределения, значимость. Источник: Медицинский словарь … Медицинские термины

Континуальное распределение Гаусса — было введено в квантовой теории поля как расширение понятия распределения Гаусса для конечномерных векторов на континуальные пространства скалярных и векторных полей. Континуальное распределение активно используется в аппарате функциональных… … Википедия

ГАУССА РАСПРЕДЕЛЕНИЕ — (Гаусса закон распределения вероятностей) то же, что нормальное распределение … Большой Энциклопедический словарь

РАСПРЕДЕЛЕНИЕ НОРМАЛЬНОЕ — наиболее важный тип распределения случайной величины. Функция Р. н. имеет вид: , где а математическое ожидание; σ2 дисперсия случайной величины; а, σ параметры Р. н. Характеристическая функция Р. н. . На практике многие случайные… … Геологическая энциклопедия

Гаусса распределение — (Гаусса закон распределения вероятностей), то же, что нормальное распределение. * * * ГАУССА РАСПРЕДЕЛЕНИЕ ГАУССА РАСПРЕДЕЛЕНИЕ (Гаусса закон распределения вероятностей), то же, что нормальное распределение (см. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ) … Энциклопедический словарь

ГАУССА РАСПРЕДЕЛЕНИЕ — (нормальное распределение) плотность распределения вероятностей случайного параметра , , равная где ср. значение, а … Физическая энциклопедия

Гаусса распределение — [Gaussian distribution] см. Нормальное распределение … Экономико-математический словарь

dic.academic.ru

Закон распределения случайных величин гаусса

Немецкий математик Гаус нашёл аналитический вид нормального закона распределения случайной величины, проявляющегося при большом числе измерений или в серии большой выборки. Вид нормального закона распределения: .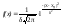

Свойства нормального закона распределения случайной величины:

Параметром функции распределения является , т.е. среднее квадратичное значение.

в центре распределения, при всех других х правее или левее центра распределения вероятность такого значения х убывает.

Функция Гаусса симметрична относительно центра распределения, т.е. при измерениях появления как меньших так и больших значениях х относительно 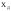равномерно.

Они показывают, что при серии измерений малой выборки закон распределения измеренной величины все более отклоняется т.е. видоизменяется относительно нормального закона.

8. Критерий нормальности распределения абсолютной погрешности при прямой измерений физической величины Х.

Измеряется прямым равноточным методом (одним прибором) некоторая физическая величина Х, истинное значение которой нам неизвестно. В процессе эксперимента находится действительное значение 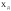, которое является оценкой её истинного значения. В качестве такой оценки при прямых значениях берётся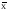, которое называется арифметическим средним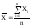. В процессе измерений находится абсолютная погрешность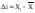. При прямом равноточном измерении сами погрешности ведут себя как случайные величины, т.е. самидолжны мало отличаться друг от друга и тогда такие погрешности случайного характера подчиняются теории ошибок, и имеют различные виды распределения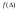. В частности при проведении выборки оказалось что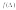подчиняется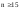нормальному закону распределения погрешности или закону Гаусса: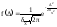(1)

— абсолютная погрешность

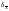— среднеарифметический от среднеквадратического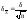

— является общей оценкой среднего арифметического, которую можно рассматривать как случайную величину. Из формулы (1) видно, что центром распределения 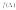, который определяется наибольшим значением функции распределения, является значение.

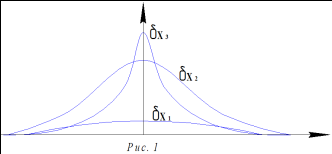
Из рис 1. можно сформулировать критерий “Нормальности” функции распределения .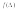

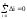— нормальный закон.

9. Доверительная вероятность и доверительный интервал. Интервал вер-ти

Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью

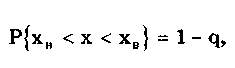
где q — уровень значимости; х_н, х_в— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра

Для получения интервальной оценки нормально распределенной случайной величины необходимо:

• определить точечную оценку МО х̅ и СКО S_x случайной величины по формулам (6.8) и (6.11) соответственно;

• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

• найти верхнюю х_в и нижнюю х_н границы в соответствии с уравнениями

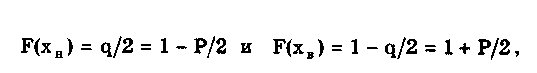
полученными с учетом (6.1). Значения х_н и х_в определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1).

Полученный доверительный интервал удовлетворяет условию

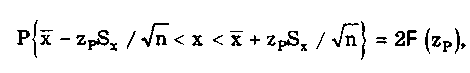(6.13)

где n — число измеренных значений; z_p — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае z_p называется квантильным множителем. Половина длины доверительного интервала 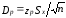называется доверительной границей погрешности результата измерений.В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Х_ц в интервал tS_x описывается неравенством Чебышева

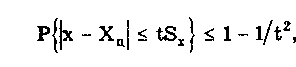
где S_x — оценка СКО распределения; t — положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6S_X. Неравенство Чебышева дает в данном случае 3,16S_X. В связи с этим оно не получило широкого распространения.Смысл понятий «доверительный интервал» и «доверительная вероятность» состоит в следующем: пусть a =0.95, тогда можно утверждать с надежностью 95%, что истинное значение величины xист не отличается от оценки (3) больше, чем на ± D xсл.

studfiles.net

Нормальный закон распределения — введение

Приветствую дорогих читателей и подписчиков блога statanaliz.info. Продолжаем разговор о распределении данных. Как мы знаем, распределение может быть эмпирическим и теоретическим. Эмпирические данные всегда ограничены своей точностью и охватом возможных ситуаций. Поэтому для расчета интересующих вероятностей, пределов отклонений, размеров выборок и т.д. используют теоретические модели распределения случайной величины.

Самая известная статистическо-вероятностная модель – это закон нормального распределения. Нормальный закон, как и другие теоретические распределения, не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. А вот конкретная форма распределения задается специальными параметрами в этом уравнении.

Например, всем понятно выражение типа у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Без заданных параметров невозможно четко представить эту линию. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами, которые «подгоняют» модель под реальные данные.

Нормальный закон в теории статистики имеет фундаментальное значение. Он также лежит в основе ряда других распределений, поэтому ухватить самую суть желательно сразу. Вначале, возможно, будет слегка мутновато, но потом станет значительно легче, обещаю. Фактически после знакомства с нормальным распределением откроются новые горизонты использования статистических методов. Кстати, собственное логическое мышление под действием статистики также начинает деформироваться, в результате чего, общение с творческими личностями превращается в испытание. Ну да ладно.

Начнем с истории. Рассказываю, как сам слышал. Возможно, где-то перепутаю века, царей или континенты. В общем, я ни разу не историк.

Краткая история открытия нормального закона

История нормального закона насчитывает уже почти 300 лет. Говорят, первым причастным к открытию стал гражданин Абрахам де Муавр, который зафиксировал свои соображения по этому поводу в далеком 1733 году. Речь тогда шла о теоретическом приближении биномиального распределения при большом количестве наблюдений. Однако труды математика не были оценены по достоинству и Абрахама несправедливо забывают, когда речь идет об открытии нормального распределения. Широкое признание нормальный закон получил благодаря анализу выборочных данных.

Сейчас всем известно, что результаты выборочного исследования всегда ошибочны относительно истинного значения, которое исследователь и пытается оценить с помощью выборки. Если провести несколько измерений, то все они, скорее всего, будут отличаться друг от друга и, соответственно, от оцениваемого показателя по генеральной совокупности.

Статистика – наука исключительно практическая. Точность выводов здесь не пустой звук, а одна из насущных задач. В то же время вариация данных не способствует решению проблемы. Например, астрономы, проводя одни и те же наблюдения за небесными телами, все время получали различные результаты. Поначалу они считали, что всему виной их собственная небрежность и старались этот факт не сильно афишировать. Однако вопрос о постоянных отклонениях торчал занозой в ученом месте и не давал покоя пытливым умам тогдашних математиков. Как же быть с тем обстоятельством, что фактически нет возможности получить однозначный результат измерений? Что делать? Куда бежать? И какой из этого следует вывод? (последний вопрос от Ослика Иа).

И вот, эволюция мысли докатилась до того, что в светлую голову гражданина по имени Даниил Бернулли пришла замечательная мысль: разброс данных у самых различных явлений имеет что-то общее. Так, он сравнил разброс отклонений в астрономических наблюдениях с разбросом попаданий лучника в мишень и обнаружил, что и там и там максимальная концентрация результатов приходится на область относительно близкую к среднему значению, в то время как значительные отклонения происходят гораздо реже. Даниил подумал: а с чего бы это? И развивая успех, предложил соответствующий математический закон. Однако на этот раз ему не фартануло – закон оказался неверным. Кстати, этот Даниил был племянником другого Бернулли по имени Якоб. Того самого, который придумал закон больших чисел и процесс своего имени (когда в некотором эксперименте имеют место только два возможных исхода: благоприятный и неблагоприятный).

Тем не менее, идея об универсальном распределении ошибок измерений не осталась не замеченной, и немного позже другие ученые все-таки сформулировали правильный закон о случайных отклонениях. К открытию стали причастны Карл Фридрих Гаусс и Пьер-Симон Лаплас.

Гаусс вывел закон о распределении ошибок, чем и увековечил память о себе названием соответствующей функции (1809 г.). Чуть позже (в 1812 г.) П. Лаплас получил интеграл, который сегодня известен как функция нормального распределения.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение. Центральная предельная теорема далее многократно уточнялась и видоизменялась, но суть ее осталась прежней. Таким образом, история открытия нормального закона насчитывает более 200 лет. Начиная от открытия Муавра, до окончательных формулировок ЦПТ в середине 20-го века. На сегодня мы имеем довольно развитый математический аппарат для анализа нормально распределенных данных.

На всякий случай еще раз отмечу, что приведенная выше история – это фривольный пересказ того, что я читал. Для серьезного изучения вопроса лучше обратиться к специализированной литературе.

Закон нормального распределения

Прежде чем погружаться в мир формул, крайне важно получить наглядное представление о предмете. Поэтому предлагаю начать с рисунка, с помощью которого далее будут изложены основные сведения о нормальном законе. Итак, функция плотности нормального распределения, она же функция Гаусса, имеет следующий вид.

Кривая Гаусса по форме несколько напоминает колокол, поэтому график нормального закона часто еще называют колоколообразной кривой. Если вдруг увидите термин «колоколообразная кривая», знайте, что речь идет о нормальном распределении.

Как видно, у графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Другими словами, вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины. Смотрим на картинку.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Теперь посмотрим на формулу, по которой нарисована колоколообразная кривая, т.е. на функцию Гаусса.

Выглядит немного пугающе, но сейчас разберемся. В функции плотности нормального распределения присутствует: две математические константы

π – соотношение длины окружности и его диаметра, равно примерно 3,142;

е – основание натурального логарифма, равно примерно 2,718;

два параметра, которые задают форму конкретной кривой

m — математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

ну и сама переменная x, для которой высчитывается значение функции, т.е. плотность вероятности.

Константы, понятное дело, не меняются. Зато параметры — это то, что придает окончательный вид конкретному нормальному распределению. Отсюда и название: параметрическая функция или семейство параметрических функций. Напомню, есть и другие теоретические распределения, но мы сейчас говорим о нормальном.

Итак, конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности, что хорошо видно на самодвижущейся картинке.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса сконцентрирована у центра. Если же у данных большой разброс, то они «размажутся» по широкому диапазону.

Плотность нормального распределения не имеет прямого практического применения (если не считать приближенных расчетов при использовании биномиального распределения). Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя свойство непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

statanaliz.info