Дроби правила переноса

Оглавление:

Дроби правила переноса

ОБОЙДИ УЖЕ ЭТИ ГРАБЛИ! 🙂

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Эта операция гораздо приятнее сложения-вычитания! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Всё предельно просто. И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо!

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы.

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет.

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но. Это решаемые проблемы.

В Особом разделе 555 «Дроби» разобраны все эти (и не только!) примеры. С подробными пояснениями что, зачем и как. Такой разбор здорово помогает при нехватке знаний и навыков!

Да и по второй проблеме там есть кое-что. ) Вполне практический совет, как стать внимательнее. Да-да! Совет, который может применить каждый.

Кроме знаний и внимательности для успеха нужен определенный автоматизм. Где его взять? Слышу тяжелый вздох… Да, только в практике, больше негде.

Можете для тренировки зайти на сайт 321start.ru. Там в опции «Попробовать» есть 10 примеров для всех желающих. С мгновенной проверкой. Для зарегистрированных пользователей — 34 примера от простых до суровых. Это только по дробям.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

www.egesdam.ru

Деление десятичных дробей

При делении десятичных дробей вам могут встретиться несколько случаев.

Деление десятичной дроби на натуральное число

Для деления десятичной дроби на натуральное число пользуемся следующими правилами.

Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
Ставим в частном запятую, когда заканчивается деление целой части делимого.

Если целая часть делимого меньше делителя, то в частном ставим 0 целых.

Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части.

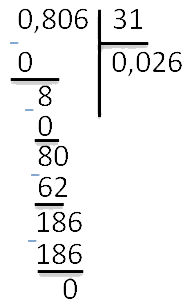
Не забываем записывать ответ в пример:

Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.

310,1 : 10 = 31,01
27,56 : 100 = 0,2756
0,75 : 10 = 0,075

Деление натурального числа на десятичную дробь

Считаем количество знаков справа от запятой в десятичной дроби.
Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., чтобы превратить десятичную дробь в целое число.
Делим числа как натуральные.
Считаем количество знако после запятой в десятичной дроби. У нас один знак. Значит, чтобы превратить 2,5 в целое число, надо умножить его на 10 . Не забываем и делимое умножить на 10 .

Деление десятичных дробей друг на друга

Делить десятичные дроби друг на друга можно разными способами. Мы опишем один из возможных. По традиции, небольшой план действий:
Определяем дробь с наибольшим количеством знаков (цифр) справа от запятой.
Умножаем обе десятичные дроби на 10, 100, 1000 и т.д., чтобы превратить десятичные дроби в целые числа.
Делим обыкновенные числа по правилам деления в столбик и записываем ответ.
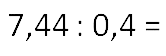
Наибольшее количество знаков (цифр) после запятой у первой десятичной дроби, поэтому ориентируемся на неё. Чтобы превратить 7,44 в целое число нужно умножить его на 100 (cм. умножение десятичных дробей).

На 10, 100, 1000 и т.д. умножаются обе десятичные дроби.
И умножаются они на одно и то же число. То есть, если вы умножили первую дробь на 10 , то и вторую вы должны умножить на 10 .

Умножаем каждую из десятичных дробей на 100.

Делим обыкновенные числа в столбик и записываем ответ. Помним, что изначально мы делили десятичные дроби.

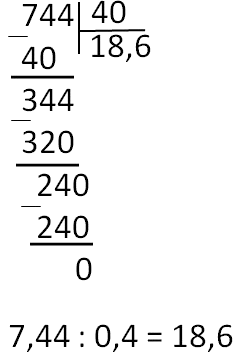
Разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д. — то же самое, что умножить её на 10, 100, 1000 и т.д. соответсвенно.
7,1 : 0,1 = 7,1 · 10 = 71
25,37 : 0,001 = 25,37 · 1 000 = 25 370
0,08 : 0,1 = 0,08 · 10 = 0,8

math-prosto.ru

Двойкам нет

Часть единицы или несколько ее частей называют простой или обыкновенной дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей — числителем. Дробь записывается в виде:

В данном случае а — числитель, b — знаменатель.

Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель больше знаменателя, то дробь больше 1, тогда дробь называется неправильной.

Если числитель и знаменатель дроби равны, то дробь равна.

1. Если числитель можно разделить на знаменатель, то эта дробь равна частному от деления:

В случае если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом, например:

Тогда 9 — неполное частное (целая часть смешанного числа),
1 — остаток (числитель дробной части),
5 — знаменатель.

Для того чтобы обратить смешанное число в дробь, необходимо умножить целую часть смешанного числа на знаменатель и прибавить числитель дробной части.

Полученный результат будет числителем обыкновенной дроби, а знаменатель останется прежним.

Действия с дробями

Расширение дроби. Значение дроби не меняется, если умножить ее числитель и знаменатель на одно и то же число, отличное от нуля.
Например:

Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля.
Например:

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, то есть привести к общему знаменателю. Рассмотрим, например, следующие дроби:

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того чтобы сложить дроби, необходимо сложить их числители, а для того чтобы вычесть дроби, надо вычесть их числители. Полученная сумма или разность будет числителем результата, а знаменатель останется прежним. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел сначала необходимо преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется к виду смешанного числа.

Умножение дробей. Для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

Деление дробей. Для того чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь.

Десятичная дробь — это результат деления единицы на десять, сто, тысячу и т.д. частей. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая — число сотых, третья — число тысячных и т. д. Цифры, расположенные после десятичной точки, называются десятичными знаками.

Например:

Свойства десятичных дробей
Десятичная дробь не меняется, если справа добавить нули: 4,5 = 4,5000.
Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: 0,0560000 = 0,056.
Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиции вправо: 4,5 45 (дробь возросла в 10 раз).
Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиции влево: 4,5 0,45 (дробь уменьшилась в 10 раз).
Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом: 0,321321321321…=0,(321)

Действия с десятичными дробями

Сложение и вычитание десятичных дробей выполняются так же, как и сложение и вычитание целых чисел, необходимо только записать соответствующие десятичные знаки один под другим.
Например:

Умножение десятичных дробей проводится в несколько этапов:
- Перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку.
- Применяется правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.
- Вынесение одного множителя за скобки: ac + bc = (a + b)c.
- Использование формул сокращенного умножения.
- Использование формулы разложения квадратного трехчлена на
где x1, x2 — корни квадратного трехчлена.
Использование теоремы Безу.
Алгебраическая дробь — это выражение вида , где A и B могут быть числом, одночленом, многочленом.

Если два выражения (числовые и буквенные) соединены знаком «=», то говорят, что они образуют равенство. Любое верное равенство, справедливое при всех допустимых числовых значениях входящих в него букв, называется тождеством.

Уравнение — это буквенное равенство, которое справедливо при определенных значениях входящих в него букв. Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в тождество, — корнями уравнения.

Решить уравнение — значит найти все его корни. Два или несколько уравнений называются равносильными, если они имеют одни и те же корни.
ноль являлся корнем уравнения;
уравнение имело только конечное число корней.

Основные типы алгебраических уравнений:

линейное: ax + b = 0;
квадратное: ax2 + bx + c = 0, a х 0;
биквадратное: ax4 + bx2 + c = 0, a х 0;
двучленное уравнение n-го порядка: xn = a, n N;
возвратное:
1. третьего порядка: ax3 + bx2 + bx + a = 0, a,b ≠ 0;
2. четвертого порядка: ax4 + bx3 + cx2 ± bx + a = 0, a,b ≠ 0.
однородное уравнение второго порядка:
af2(x) + bf(x)g(x) + cg2(x) =0, a х 0, b2 + c2 > 0;
уравнение вида: f(x)g(x) = 0;
уравнение вида: ; уравнение вида: f((x)) = 0.

У линейного уравнения ax + b = 0:

если a х 0, имеется единственный корень x = —b/a;
если a = 0, b ≠ 0, нет корней;
если a = 0, b = 0, корнем является любое действительное число.

Уравнение xn = a, n N:

если n — нечетное число, имеет при любом а действительный корень, равный a/n;
если n — четное число, то при a 0, то имеет два корня.

Основные тождественные преобразования: замена одного выражения другим, тождественно равным ему; перенос членов уравнения из одной стороны в другую с обратными знаками; умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля.

Линейным уравнением с одним неизвестным называется уравнение вида: ax+b=0, где a и b — известные числа, а x — неизвестная величина.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

, где a, b, c, d, e, f — заданные числа; x, y — неизвестные.

Числа a, b, c, d — коэффициенты при неизвестных; e, f — свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами: метод подстановки: из одного уравнения выражаем одно из неизвестных через коэффициенты и другое неизвестное, а затем подставляем во второе уравнение, решая последнее уравнение, находим сначала одно неизвестное, затем подставляем найденное значение в первое уравнение и находим второе неизвестное; метод сложения или вычитания одного уравнения из другого.

Операции с корнями:

Арифметическим корнем n-й степени из неотрицательного чис-ла a называется неотрицательное число, n-я степень которого рав-на a. Алгебраическим корнем n-й степени из данного числа называ-ется множество всех корней из этого числа.

Иррациональные числа в отличие от рациональных не могут быть представлены в виде обыкновенной несократимой дроби вида m/n, где m и n — целые числа. Это числа нового типа, которые могут быть вычислены с любой точностью, но не могут быть заменены рациональным числом. Они могут появиться как результат геометрических измерений, например: отношение длины диагонали квадрата к длине его стороны равно.

Квадратное уравнение есть алгебраическое уравнение второй степени ax2+bx+c=0, где a, b, c — заданные числовые или буквенные коэффициенты, x — неизвестное. Если разделить все члены этого уравнения на а, в результате получим x2+px+q=0 — приведенное уравнение p=b/a, q=c/a. Его корни находятся по формуле:

Если b2—4ac>0, тогда имеются два различных корня, b2— 4ac=0, тогда имеются два равных корня; b2—4ac

xn—-7sbfhivhrke5c.xn--p1ai

Сложные выражения с дробями. Порядок действий

Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?

В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:

Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
Затем — деление и умножение;
Последним шагом выполняется сложение и вычитание.

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.

Задача. Найдите значения выражений:

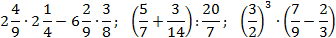
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

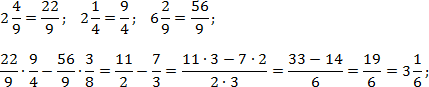
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2 . Тогда:

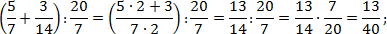
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3 , имеем:

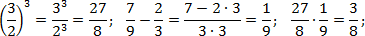
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.

Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:

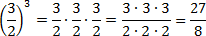
Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

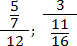
Здесь и далее мы будем называть эти дроби многоэтажными . Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

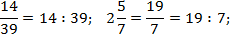
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

Задача. Переведите многоэтажные дроби в обычные:

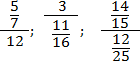
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:

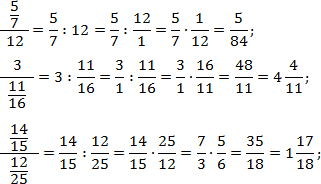
В последнем примере перед окончательным умножением дроби были сокращены.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

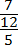
Это выражение можно прочитать по-разному:

В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

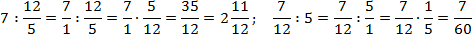
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

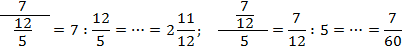
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

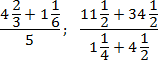
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

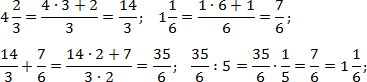
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

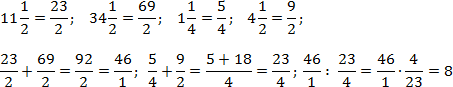
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

www.berdov.com

Miassats.Ru

Дроби правила переноса

Дроби правила переноса

Умножение и деление дробей.

Если Вам нравится этот сайт.

Деление десятичных дробей

Деление десятичной дроби на натуральное число

Деление натурального числа на десятичную дробь

Деление десятичных дробей друг на друга

Двойкам нет

Действия с дробями

Свойства десятичных дробей

Действия с десятичными дробями

Свойства абсолютной величины

Сложные выражения с дробями. Порядок действий

Многоэтажные дроби

Специфика работы с многоэтажными дробями

Юридические вопросы и ответы