Оглавление:
Линейная алгебра
для чайников

Отсутствие рекламы стоит $72=5600 рублей в год.
Уменьшеный объём рекламы стоит $36=2800 рублей в год.

Сколькими усадьбами владеет премьер-министр Медведев? Узнайте из расследования Фонда по борьбе с коррупцией. Вот видеоверсия. А здесь текстовый вариант.
Содержание:
Чтобы изучить линейную алгебру, вы можете прочесть и вникнуть в книгу И. В. Белоусова «Матрицы и определители». Однако она написана строгим и сухим математическим языком, который людям со средним умом воспринимать тяжело. Поэтому я сделал пересказ наиболее трудных для понимания мест этой книги, стараясь изложить материал как можно понятнее, максимально используя для этого рисунки. Доказательства теорем я опустил. Признаться, я и сам не стал в них вникать. Верю г-ну Белоусову! Судя по его работе, он грамотный и толковый математик. Скачать его книгу можно по адресу http://eqworld.ipmnet.ru/ru/library/books/Belousov2006ru.pdf Если собираетесь вникать в мою работу, это нужно сделать, потому что я буду на Белоусова часто ссылаться.

Начнём с определений. Что такое матрица? Это прямоугольная таблица чисел, функций или алгебраических выражений. Зачем нужны матрицы? Они сильно облегчают сложные математические расчёты. У матрицы можно выделить строки и столбцы (рис. 1).

Строки и столбцы нумеруются, начиная слева сверху (рис. 1-1). Когда говорят: матрица размером m n (или m на n), подразумевают под m количество строк, а под n количество столбцов. Например, матрица на рисунке 1-1 имеет размер «4 на 3», а не «3 на 4».

Смотрите на рис. 1-3, какие бывают матрицы. Если матрица состоит из одной строки, она называется матрицей–строкой, а если из одного столбца, то матрицей–столбцом. Матрица называется квадратной n–го порядка, если число строк у неё равно числу столбцов и равно n. Если все элементы матрицы равны нулю, то это нулевая матрица. Квадратная матрица называется диагональной, если равны нулю все её элементы, кроме расположенных на главной диагонали.

Сразу объясняю, что такое главная диагональ. На ней номера строк и столбцов одинаковые. Идёт она слева направо сверху вниз. (рис. 3) Элементы называются диагональными, если они расположены на главной диагонали. Если все диагональные элементы равны единице (а остальные нулю), матрица называется единичной. Две матрицы A и B одинакового размера называются равными, если все их элементы одинаковые.
2 Операции над матрицами и их свойства


Умножение матриц.


Умножение двух матриц определено лишь тогда (в переводе на русский: матрицы можно умножать лишь тогда), когда число столбцов первой матрицы в произведении равно числу строк второй (рис. 7 , наверху, синие скобки). Чтобы лучше запомнить: цифра 1 больше похожа на столбец. В результате умножения получается матрица размером (смотри рисунок 6). Чтобы было проще запомнить, что на что надо умножать, предлагаю следующий алгоритм: смотрим рисунок 7. Умножаем матрицу A на матрицу B. У матрицы A два столбца, у матрицы B две строки — умножать можно.
1) Займёмся первым столбиком матрицы B (он у неё один только и есть). Записываем этот столбик в строку (транспонируем столбик, о транспонировании чуть ниже).
2) Копируем эту строку, чтобы у нас получилась матрица размером с матрицу A.
3) Умножаем элементы этой матрицы на соответствующие элементы матрицы A.
4) Складываем получившиеся произведения в каждой строчке и получаем матрицу-произведение из двух строк и одного столбца.

На рисунке 7-1 даны примеры умножения матриц, которые размером поболее.
1) Здесь у первой матрицы три столбца, значит у второй должно быть три строчки. Алгоритм ровно тот же, что в предыдушем примере, только тут в каждой строчке три слагаемых, а не два.
2) Здесь у второй матрицы два столбца. Сначала проделываем алгоритм с первым столбцом, затем со вторым, и получаем матрицу «два на два».
3) Тут у второй матрицы столбец состоит из одного элемента, от транспонирования столбец не изменится. И складывать ничего не надо, так как в первой матрице всего один столбец. Проделываем алгоритм три раза и получаем матрицу «три на три».
Имеют место следующие свойства:
1. Если сумма B + C и произведение AB существуют, то A (B + C ) = AB + AC
2. Если произведение AB существует, то x (AB) = (xA) B = = A (xB).
3. Если произведения AB и BC существуют, то A (BC) = (AB) C .
Если произведение матриц AB существует, то произведение BA может не существовать.
Если даже произведения AB и BA существуют, то они могут оказаться матрицами разных размеров.
Оба произведения AB и BA существуют и являются матрицами одинакового размера лишь в случае квадратных матриц A и B одного и того же порядка. Однако, даже в этом случае AB может не равняться BA.
Возведение в степень
Транспонирование матриц
Симметричные и антисимметричные матрицы
Ты как здесь оказался?
Не понял, что преподаватель объяснял?

Я тебя научу, как учиться, чтобы понимать. Кликай сюда!

Как учиться эффективно. Практические советы
3 Определители квадратных матриц
Что такое определитель матрицы? Это такое число, которое вычисляется при помощи специальных операций с (квадратной!) матрицей. При расчётах в зависимости от значения определителя можно делать важные выводы, например, перпендикулярны или нет прямые.
 Определителем |A| матрицы первого порядка A , или определителем первого порядка, называется число , равное матричному элементу
Определителем |A| матрицы первого порядка A , или определителем первого порядка, называется число , равное матричному элементу
Определителем |A| матрицы второго порядка , или определителем второго порядка, называется число , определяемое формулой (смотрите рис. 12) . То есть, чтобы найти этот определитель, перемножаем элементы главной диагонали и вычитаем из них произведение оставшихся. Первая цифра индекса элемента на рисунке (выделена голубым) означает номер его строки, а вторая цифра, выделенная жёлтым, — номер столбца. Скобками выделены члены определителя.
Найти определитель матрицы третьего порядка (определитель третьего порядка) гораздо сложней. Далее изложен один из способов вычисления определителя третьего порядка. Другие способы изожены в разделах 5 и 6.  Сначала объясню некоторые понятия, которые понадобятся при вычислении. Представьте себе последовательность чисел (именно вот с такими элементами, в таком порядке): (рис. 10).
Сначала объясню некоторые понятия, которые понадобятся при вычислении. Представьте себе последовательность чисел (именно вот с такими элементами, в таком порядке): (рис. 10).
Теперь представьте себе вторую последовательность чисел: Чему равны эти числа из второй последовательности? Смотрим рис. 10. Каждое из чисел второй последовательности равно какому — то из чисел первой последовательности, причём одинаковых чисел во второй последовательности нет. Я выражусь может быть не очень правильно с точки зрения строгой математики, но более понятно: вторая последовательность — это та же первая последовательность, с теми же самыми элементами, но расположенными в ином порядке. Вот эта вторая последовательность называется перестановкой степени 6. Из чисел второй последовательности, то бишь перестановки можно образовать всевозможные пары, например: (a1=4 , a3=3); (a5=6 , a4=2); (a2=1 , a6=5); (a5=6 , a1=4). Теперь смотрите на рисунок 10. Если один элемент больше другого, а индекс его, наоборот, меньше, чем у другого, то такая пара называется инверсией.
 Белоусов описал простой способ нахождения числа инверсий в перестановке. Смотрим рисунок 11. Находим в перестановке число 1 и считаем, сколько чисел слева от него. Запоминаем или записываем. Затем число 1 зачёркиваем. Зачёркнутые числа в дальнейших подсчётах не учитываются. Далее находим число 2, считаем, сколько незачёркнутых чисел слева от него. Запоминаем или записываем. Число 2 зачёркиваем. Затем находим число 3 и проделываем те же операции, что с числами 1 и 2. И так проходим все числа перестановки. Затем те числа, которые мы запомнили или записали, суммируем. Получаем число инверсий в перестановке.
Белоусов описал простой способ нахождения числа инверсий в перестановке. Смотрим рисунок 11. Находим в перестановке число 1 и считаем, сколько чисел слева от него. Запоминаем или записываем. Затем число 1 зачёркиваем. Зачёркнутые числа в дальнейших подсчётах не учитываются. Далее находим число 2, считаем, сколько незачёркнутых чисел слева от него. Запоминаем или записываем. Число 2 зачёркиваем. Затем находим число 3 и проделываем те же операции, что с числами 1 и 2. И так проходим все числа перестановки. Затем те числа, которые мы запомнили или записали, суммируем. Получаем число инверсий в перестановке.
А зачем нужно знать число инверсий в перестановке? У перестановки есть такая характеристика, как знак перестановки, или, не по русски, сигнатура перестановки (обозначается как sign). Так вот, если число инверсий в перестановке чётное, sign=1, и сама перестановка называется чётной. А если число инверсий в перестановке нечётное, sign=-1, и перестановка называется, соответственно, нечётной. Для тех, кому особо интересно, излагаю, как вычисляется этот знак перестановки. Он равен (-1) (число инверсий) Если число инверсий чётное, знак равен 1, если нечётное, то -1 .

Смотрим рис. 13, позиция 1 . На нём матрица и её определитель. Внимательно рассмотрим определитель. Рассмотрим какой-нибудь его член. Он состоит из трёх элементов. Посмотрите на первые цифры их индексов (голубые, означают номера строк). Теперь так же посмотрите на другие члены определителя. Вы видите закономерность ? В каждом члене определителя первые цифры образуют последовательность 1, 2, 3. То есть первый элемент члена определителя находится на первой строке, второй на второй, третий на третьей. Теперь посмотрите на жёлтые индексы, то бишь номера столбцов. А здесь какая закономерность, и чем она отличается от предыдушей? В каждом члене определителя одинаковых жёлтых номеров нет. Это значит, в каждом члене определителя элементы находятся на разных столбцах. В каждом члене определителя есть и 1, и 2, и 3, но они «перемешаны», то есть образуют перестановку. Вот каждому возможному варианту этой перестановки и соответствует член определителя. Я это попытался графически изобразить на рис. 13 . позиция 2. Смотрим снова на определитель. Некоторые его члены прибавляются к общей сумме, то есть имеют положительный знак, другие, наоборот, отнимаются, (знак их отрицательный). Как определить, прибавлять член или отнимать? А вот как — смотрим на жёлтые индексы. В каждом члене они образуют перестановку. То, что я вам толковал про инверсии и знак перестановки, ещё не вылетело у вас из головы? Если вылетело, снова изучите рис.11, перечитайте соответствующий абзац. Вычисляем знак перестановки. Если он положительный, член определителя прибавляется, если отрицательный — отнимается. Белоусов предлагает более удобный способ определить знак члена определителя. Смотрим рис. 13, позиция 3. Один член выделен синим, определяем его знак. Соединяем элементы отрезками (всеми возможными способами). Смотрим на рисунок. Два отрезка имеют так называемый положительный наклон, один — отрицательный. Что такое положительный наклон отрезка? Если в нём направление перехода на большую строку совпадает с направлением перехода на больший столбец, наклон отрезка положительный, если не совпадает — отрицательный. Отрезок с отрицательным наклоном соответствует инверсии в перестановке. Не поняли? Помозгуйте. Так вот, если число отрезков с отрицательным наклоном чётное, член определителя прибавляется, если нечётное, то вычитается.
Можете посмотреть, что такое определитель, определение его то бишь, у Белоусова на стр. 32 . После определения у Белоусова следуют примеры, внимательно их изучите, разжёвывать их мне неохота. Мы можем сделать некоторые важные выводы. Если какая–либо строка (или столбец) квадратной матрицы состоит из одних нулей, этот нуль входит множителем во все члены определителя, следовательно определитель равен нулю. После определения у Белоусова следуют примеры, внимательно их изучите, разжёвывать их мне неохота.

Посчитаем определитель какой — нибудь диагональной матрицы. Огого! Да у нас только один член определителя, который состоит только из диагональных элементов, не равен нулю! Делаем важный вывод: Определитель диагональной матрицы равен произведению её диагональных элементов. А следовательно определитель единичной матрицы равен 1.
4 Свойства определителей
5. Определитель произведения матриц
Привожу без доказательств теорему, которая доказана в работе Белоусова, и следствия из неё.
Теорема: Определитель произведения двух (а также нескольких) квадратных матриц одного и того же порядка равен произведению их определителей.
Следствие: Определитель целой положительной степени квадратной матрицы равен определителю этой матрицы, возведённому в ту же степень.
Обратите внимание: если при умножении матрицы переставить местами, в результате получатся разные матрицы. Однако согласно теореме, определитель у них будет одинаковый.
5. Миноры и алгебраические дополнения

Что такое минор? Возьмём какой нибудь элемент квадратной матрицы, например, элемент A22 на рисунке 15-1, позиция 1. Если у матрицы убрать строку, на которой расположен этот элемент, а также столбец, на котором расположен этот элемент, мы получим матрицу меньшего размера. Определитель этой матрицы и называется минором элемента (обозначается греческой буквой «мю»). Обратите внимание, что минор элемента вычислить гораздо легче, чем определитель матрицы. Если матрица второго порядка (рис. 15-1, позиция 2), то минор элемента и вовсе равен одному из других элементов.
Введём ещё понятие — алгебраическое дополнение элемента. Величина алгебраического дополнения зависит от суммы номеров столбца и строки, на которых расположен элемент. Если эта сумма чётная, алгебраическое дополнение равно минору элемента, если нечётная — то минору, взятому с отрицательным знаком. Обозначается алгебраическое дополнение греческой буквой «альфа».

Замечание 5.1 Его формулировку на математическом языке и доказательство смотрите у Белоусова. Я же изложу его «простым» языком. Если матрицу транспонировать, алгебраические дополнения её элементов (переместившихся на другие «места») останутся прежними. Смотрите рисунок 15-2.
Теорема 5.1 Определитель квадратной матрицы равен сумме произведений элементов любой строки на их алгебраические дополнения. Важнейшая теорема! На ней основан эффективный способ нахождения определителей.

Эта теорема подтверждает следствие 1 теоремы 4.3. Смотрим рис. 15-3. Две матрицы различаются только одной строкой, причём соответствующие элементы этой строки у матрицы C в два раза больше, чем у матрицы B. Если вычислить определители матриц через алгебраические дополнения этих строк, определитель матрицы C окажется в два раза больше матрицы B. Вывод: Общий множитель всех элементов строки матрицы можно вынести за знак определителя.
Теорема 5.2 Сумма произведений элементов какой-либо строки определителя n–го порядка на алгебраические дополнения элементов другой его строки равна нулю.
Теоремы 5.1 и 5.2 в равной степени применимы как строкам, так и к столбцам матрицы.
6. Вычисление определителей
6.1 Приведение матрицы к треугольному виду
6.2 Понижение порядка определителя.

Сначала повторите теорему 5.1 и её следствие, а также следствия 1 и 3 теоремы 4.3 Будем вычислять определитель матрицы пятого порядка (рис. 16-0). В четвёртом столбике у неё имеется два нуля, что весьма кстати. Определитель можно вычислить через алгебраические дополнения элементов этого столбика. Чтобы уменьшить объём вычислений, сначала добъёмся, чтобы все элементы этого столбика, кроме одного, были равны нулю.
2) Умножили вторую строку на -1 и прибавили к первой.
3) Умножили пятую строку на -3 и прибавили ко второй.
4) Понижаем порядок определителя. Сумма номеров столбца (четвёртый) и строки (пятая) является нечётной, поэтому определитель пятого порядка равен -2 определителя четвёртого порядка.
5) Работаем со вторым столбиком определителя четвёртого порядка. Четвёртую строку прибавили ко второй.
6) Третью строку умножили на -7 и прибавили к четвёртой.

7) Третью строку умножили на 2 и прибавили к первой.
8) Понижаем порядок определителя. Сумма номеров третьей строки и второго столбика является нечётной, поэтому определитель пятого порядка равен 2 определителя третьего порядка.
9) Умножили первую строку на 2 и прибавили к третьей.
10) Вынесли общий множитель второй строки за знак определителя.
11) Выносим общий множитель третьей строки за знак определителя.
12) Теперь вспомним, что строки и столбцы у нас равноправны. Делаем «разложение определителя третьего порядка по элементам третьей строки». В третьей строке два элемента не равны нулю, и нам придётся вычислить два определителя второго порядка. В результате у меня получилось 1128. Посмотрите ещё примеры у Белоусова на стр. 56 — 58.
7 Обратные матрицы
Чтобы найти обратную матрицу, можно проделать следущее:
1) Найти определитель исходной матрицы. Если он равен нулю, матрица вырожденная, и обратной к ней матрицы не существует.
2)Транспонировать исходную матрицу.
3)Заменить в получившейся матрице все элементы их алгебраическими дополнениями.
4)Умножить получившуюся матрицу на число 1/A , где A — определитель исходной матрицы.
Однако есть более простые способы.
Метод нахождения обратной матрицы при помощи элементарных преобразований строк.
На рис. 16-1, позиция 1) изображена так называемая расширенная матрица. Она состоит из двух подматриц. Слева — исходная, к ней мы будем находить обратную матрицу. Справа — единичная матрица. С ней мы будем проделывать ровно те же операции, что и с исходной матрицей, и в результате исходная матрица превратится в единичную, а единичная — в обратную к исходной.
Операции будем проводить следущие:
1) Умножение любой строки на число X, не равное нулю.
2) Прибавление любой строки, умноженной на число X, к другой строке. При этом остальные строки не меняются.
3) Перестановка двух строк между собой. При этом остальные строки не меняются
Почему именно эти операции, и почему в результате получится обратная матрица? Желающие докопаться до ответа на эти вопросы могут обратиться к работе Белоусова (глава 7).

Будем добиваться. чтобы в нули превратились все недиагональные элементы сначала в первом столбике, затем во втором, и так далее (впрочем, это не принципиально).
2) Умножили вторую строку на (-3) и прибавили к третьей строке.
3) Поменяли местами первую и вторую строки.
4)Умножили первую строку на (-2) и прибавили ко второй строке.
5) Умножили вторую строку на (-1) и прибавили к третьей строке.
6) Прибавили третью строку к первой строке.
7) Умножили третью строку на -1/2 .
8) Умножили третью строку на 3 и прибавили ко второй. Слева получаем единичную матрицу, справа — обратную к исходной
В работе Белоусова имеется несколько примеров нахождения обратных матриц таким способом (раздел 7.2). Рекомендую их посмотреть.
7.3 Нахождение обратной матрицы методом Жордана–Гаусса
7.4 Свойства невырожденных матриц
Белоусов в своей работе доказывает несколько свойств:
1) Если определитель матрицы равен x (x не равно нулю), определитель обратной к ней матрицы равен 1/x. Это следует из того, что определитель единичной матрицы равен 1.
2) (A -1 ) -1 =A Матрица, обратная к обратной — та же самая матрица.
3) (A m ) -1 =(A -1 ) m Если найти матрицу, обратную матрице A, а потом эту обратную матрицу (A -1 ) возвести в степень m, в итоге получится такая же матрица, которая получится, если проделать эти операции в другом порядке: сначала матрицу A возвести в степень m, а затем найти матрицу, обратную к A m .
4) (AB) -1 =B -1 A -1 Если две матрицы перемножить, а затем найти обратную к получившейся матрице, в итоге получится та же матрица, которая получится после умножения двух матриц, обратных к первоначальным.
5) (A -1 ) T =(A T ) -1 Если найти матрицу, обратную матрице A, а потом эту обратную матрицу (A -1 ) транспонировать, в итоге получится такая же матрица, которая получится, если проделать эти операции в другом порядке: сначала транспонировать матрицу A, а затем найти обратную к транспониорванной.
8 Ранг матрицы
9 Линейная зависимость строк и столбцов матрицы
Вы помните, как выполняются арифметические действия со строками матрицы? Чтобы сложить две строки, складываем соотвествующие их элементы и получаем строку с элементами, равными сумме слагаемых элементов. Чтобы умножить строку на число, умножаем каждый элемент на это число и получаем строку с произведениями.

Смотрим матрицу из двух столбиков на рис. 19, позиция 1. Строку C можно получить, если строку A умножить на 2 и прибавить к строке B(19, поз. 1, 1). Говорят, что строка C является линейной комбинацией строк A и B. Частным случаем линейной комбинации является сумма строк и умножение строки на число (рис. 19, поз. 2). Вернёмся к строке C. Она получается из строк A и B. Следует ли из этого, что строку A можно получить из строк B и C? Следует (19, поз. 1-2). То есть строка А является линейной комбинацией строк B и C. Также и строка B является линейной комбинацией строк A и C (19, поз. 1-3). А вот ещё линейная комбинация из этих строк (19, поз. 1-4). Строка N состоит из одних нулей, то есть это нулевая строка. Строки A, B, C являются линейно зависимыми. Что это означает? Согласно определению линейной зависимости строк, найдутся такие числа (a=2, b=1,c=-1,), не равные одновременно нулю что линейная комбинация строк aA+bB+cC будет равна нулевой строке. Обратите внимание на требование, чтобы числа (a, b, c) не были равны одновременно нулю. Без него понятие линейной зависимости теряет смысл. Можно взять какие угодно строки. Если все коэффициенты при них будут равны нулю (19, поз. 1-5), их линейная комбинация, естественно, будет равна нулевой строке. Однако часть коэффициентов может быть равна нулю. Добавим к линейной комбинации (19, поз. 1-4) строку D, умноженную на 0 (19, поз. 1-6). Равенство осталось верным. Поэтому можно отнести к линейно зависимым строкам и строку D, какая бы она ни была. Мы можем сделать важный вывод: если часть строк линейно зависимы, то и все они линейно зависимы.
В книге Белоусова доказываются следущие утверждения:
Строки единичной матрицы (19, поз. 3) линейно независимы.
Замечание: Характер линейных зависимостей матрицы не меняется при произвольной перестановке её строк или столбцов.
Теорема 9.1: Строки матрицы зависимы тогда и только тогда, когда одна из них является линейной комбинацией остальных строк (19, поз. 1-4) и (19, поз. 1-1, 1-2, 1-3).
Теорема 9.2: Если часть строк линейно зависимы, то и все они линейно зависимы (19, поз. 1-1) и (19, поз. 1-6).
Следствие1: Если среди строк матрицы имеется нулевая строка, то эти строки линейно зависимы. В самом деле, если взять нулевую строку с каким угодно коэффициентом, не равным нулю, а остальные с нулевыми коэффициентами, получится нулевая строка (19, поз. 1-7).
Следствие 2 Если среди строк матрицы имеются пропорциональные, то все они линейно зависимы (19, поз. 2).
Замечание 9.2 Понятие линейной зависимости (а стало быть, и приведённые выше теоремы и следствия) применимо не только к строкам, но и к столбцам матрицы.
10 Теорема о базисном миноре
11 Подсчёт ранга матрицы и нахождение базисного минора
alik-abdulin.narod.ru
Векторы для чайников. Действия с векторами.
Координаты вектора. Простейшие задачи с векторами
Наконец-то у меня добрались руки до обширной и долгожданной темы аналитической геометрии. Сначала немного о данном разделе высшей математики…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает прилагательное «аналитическая»? На ум сразу приходят два штампованных математических оборота: «графический метод решения» и «аналитический метод решения». Графический метод, понятно, связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решений практически всех задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
Открываемый курс уроков по геометрии не претендует на теоретическую полноту, он ориентирован на решение практических задач. Я включу в свои лекции только то, что с моей точки зрения, является важным в практическом плане. Если вам необходима более полная справка по какому-либо подразделу, рекомендую следующую вполне доступную литературу:
1) Вещь, с которой, без шуток, знакомо несколько поколений: Школьный учебник по геометрии, авторы – Л.С. Атанасян и Компания. Сия вешалка школьной раздевалки уже выдержала 20-ть (!) переизданий, что, конечно, не является пределом.
2) Геометрия в 2 томах. Авторы Л.С. Атанасян, Базылев В.Т. Это литература для высшей школы, вам потребуется первый том. Из моего поля зрения могут выпадать редко встречающиеся задачи, и учебное пособие окажет неоценимую помощь.
Обе книги можно бесплатно закачать в Интернете. Кроме того, можете использовать мой архив с готовыми решениями, который можно найти на странице Скачать примеры по высшей математике.
Из инструментальных средств предлагаю опять же собственную разработку – программный комплекс по аналитической геометрии, который значительно упростит жизнь и сэкономит массу времени.
Предполагается, что читатель знаком с базовыми геометрическими понятиями и фигурами: точка, прямая, плоскость, треугольник, параллелограмм, параллелепипед, куб и т.д. Желательно помнить некоторые теоремы, хотя бы теорему Пифагора, привет второгодникам)
А сейчас мы последовательно рассмотрим: понятие вектора, действия с векторами, координаты вектора. Далее рекомендую прочитать важнейшую статью Скалярное произведение векторов, а также Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. Не лишней будет и локальная задача – Деление отрезка в данном отношении. На основе вышеуказанной информации можно освоить уравнение прямой на плоскости с простейшими примерами решений, что позволит научиться решать задачи по геометрии. Также полезны следующие статьи: Уравнение плоскости в пространстве, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость, другие разделы аналитической геометрии. Естественно, попутно будут рассматривать типовые задания.
Понятие вектора. Свободный вектор
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
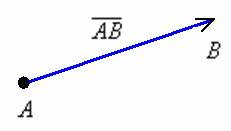
В данном случае началом отрезка является точка 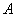 , концом отрезка – точка
, концом отрезка – точка 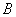 . Сам вектор обозначен через
. Сам вектор обозначен через 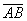 . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор
. Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор 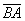 , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.
, и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором 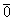 . У такого вектора конец и начало совпадают.
. У такого вектора конец и начало совпадают.
. Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении 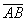 и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой:
и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: 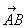 , но допустима и запись
, но допустима и запись 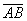 , которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе. В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом:
, которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе. В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: 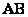 , подразумевая тем самым, что это вектор.
, подразумевая тем самым, что это вектор.
То была стилистика, а сейчас о способах записи векторов:
1) Векторы можно записать двумя большими латинскими буквами:
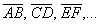 и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
2) Векторы также записывают маленькими латинскими буквами:
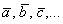 В частности, наш вектор
В частности, наш вектор 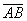 можно для краткости переобозначить маленькой латинской буквой
можно для краткости переобозначить маленькой латинской буквой 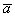 .
.
Длиной или модулем ненулевого вектора 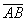 называется длина отрезка
называется длина отрезка 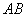 . Длина нулевого вектора
. Длина нулевого вектора 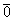 равна нулю. Логично.
равна нулю. Логично.
Длина вектора обозначается знаком модуля: 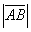 ,
, 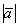
Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.
То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.
Если совсем просто – вектор можно отложить от любой точки:
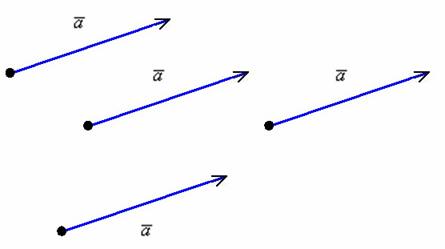
Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте вектор произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё математически корректно – вектор можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)
Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения вектора имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия. Впрочем, несвободные векторы встречаются и в курсе вышмата (не ходите туда :)).
Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора 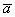 и
и 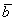 :
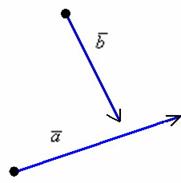
:
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 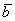 от конца вектора
от конца вектора 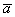 :
:
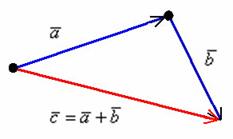
Суммой векторов 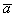 и
и 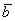 является вектор
является вектор 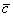 . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору
. Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору 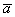 , а затем по вектору
, а затем по вектору 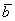 . Тогда сумма векторов
. Тогда сумма векторов 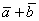 представляет собой вектор результирующего пути
представляет собой вектор результирующего пути 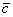 с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
Кстати, если вектор 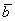 отложить от начала вектора
отложить от начала вектора 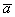 , то получится эквивалентное правило параллелограмма сложения векторов.
, то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: 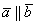 , при этом возможна детализация:
, при этом возможна детализация: 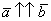 (векторы сонаправлены) или
(векторы сонаправлены) или 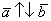 (векторы направлены противоположно).
(векторы направлены противоположно).
Произведением ненулевого вектора 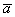 на число
на число 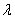 является такой вектор
является такой вектор 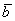 , длина которого равна
, длина которого равна 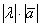 , причём векторы
, причём векторы 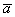 и
и 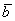 сонаправлены при
сонаправлены при 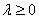 и противоположно направлены при
и противоположно направлены при 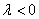 .
.
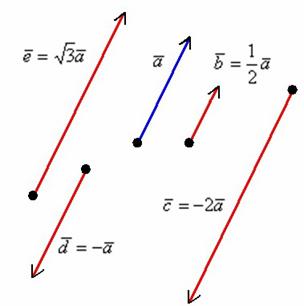
Правило умножения вектора на число легче понять с помощью рисунка:
Разбираемся более детально:
1) Направление. Если множитель  отрицательный, то вектор меняет направление на противоположное.
отрицательный, то вектор меняет направление на противоположное.
2) Длина. Если множитель заключен в пределах 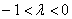 или
или 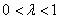 , то длина вектора уменьшается. Так, длина вектора
, то длина вектора уменьшается. Так, длина вектора 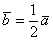 в два раза меньше длины вектора
в два раза меньше длины вектора 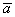 . Если множитель
. Если множитель 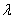 по модулю больше единицы, то длина вектора увеличивается в
по модулю больше единицы, то длина вектора увеличивается в 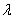 раз.
раз.
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, 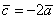 . Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.
. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.
4) Векторы 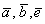 сонаправлены. Векторы
сонаправлены. Векторы 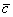 и
и 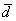 также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
Координаты вектора на плоскости и в пространстве
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы  и
и 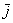 :
:
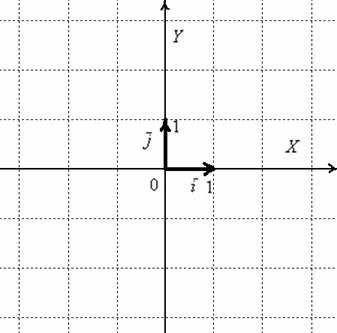
Векторы 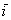 и
и 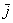 ортогональны. Ортогональны = Перпендикулярны. Рекомендую потихоньку привыкать к терминам: вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.
ортогональны. Ортогональны = Перпендикулярны. Рекомендую потихоньку привыкать к терминам: вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.
Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: 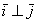 .
.
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.
Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 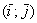 . Координатные векторы нельзя переставлять местами.
. Координатные векторы нельзя переставлять местами.
Любой вектор 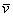 плоскости единственным образом выражается в виде:
плоскости единственным образом выражается в виде:
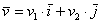 , где
, где 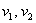 – числа, которые называются координатами вектора в данном базисе. А само выражение
– числа, которые называются координатами вектора в данном базисе. А само выражение 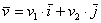 называется разложением вектора
называется разложением вектора 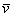 по базису
по базису 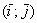 .
.
! ВСЕМ настоятельно рекомендую прочитать ВСЁ!
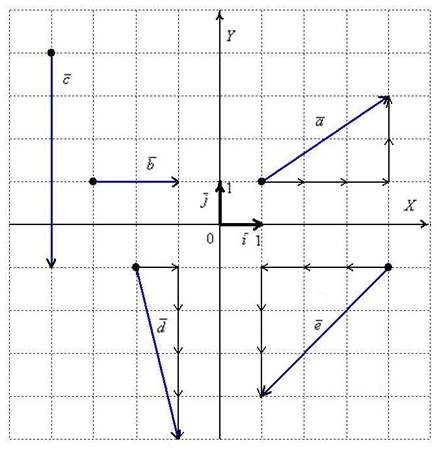
Начнем с первой буквы 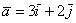 алфавита: . По чертежу хорошо видно, что при разложении вектора по базису используются только что рассмотренные:
алфавита: . По чертежу хорошо видно, что при разложении вектора по базису используются только что рассмотренные:
1) правило умножения вектора на число: 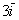 и
и 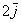 ;
;
2) сложение векторов по правилу треугольника: 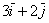 .
.
А теперь мысленно отложите вектор 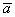 от любой другой точки плоскости. Совершенно очевидно, что его разложение
от любой другой точки плоскости. Совершенно очевидно, что его разложение 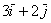 будет «неотступно следовать за ним». Вот она, свобода вектора – вектор «всё носит при себе». Это свойство, разумеется, справедливо для любого вектора. Забавно, что сами базисные (свободные) векторы
будет «неотступно следовать за ним». Вот она, свобода вектора – вектор «всё носит при себе». Это свойство, разумеется, справедливо для любого вектора. Забавно, что сами базисные (свободные) векторы 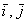 не обязательно откладывать от начала координат, один можно нарисовать, например, слева внизу, а другой – справа вверху, и от этого ничего не изменится! Правда, делать так не нужно, поскольку преподаватель тоже проявит оригинальность и нарисует вам «зачтено» в неожиданном месте.
не обязательно откладывать от начала координат, один можно нарисовать, например, слева внизу, а другой – справа вверху, и от этого ничего не изменится! Правда, делать так не нужно, поскольку преподаватель тоже проявит оригинальность и нарисует вам «зачтено» в неожиданном месте.
Векторы 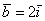 ,
, 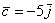 иллюстрируют в точности правило умножения вектора на число, вектор
иллюстрируют в точности правило умножения вектора на число, вектор 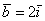 сонаправлен с базисным вектором
сонаправлен с базисным вектором 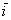 , вектор
, вектор 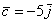 направлен противоположно по отношению к базисному вектору
направлен противоположно по отношению к базисному вектору 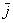 . У данных векторов одна из координат равна нулю, дотошно можно записать так:
. У данных векторов одна из координат равна нулю, дотошно можно записать так:
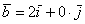
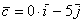
А базисные векторы, к слову, так: 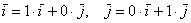 (по сути, они выражаются сами через себя).
(по сути, они выражаются сами через себя).
И, наконец: 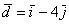 ,
, 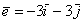 . Кстати, что такое вычитание векторов, и почему я не рассказал о правиле вычитания? Где-то в линейной алгебре, уже не помню где, я отмечал, что вычитание – это частный случай сложения. Так, разложения векторов «дэ» и «е» преспокойно записываются в виде суммы:
. Кстати, что такое вычитание векторов, и почему я не рассказал о правиле вычитания? Где-то в линейной алгебре, уже не помню где, я отмечал, что вычитание – это частный случай сложения. Так, разложения векторов «дэ» и «е» преспокойно записываются в виде суммы: 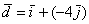 ,
, 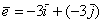 . Переставьте слагаемые местами и проследите по чертежу, как чётко в этих ситуациях работает старое доброе сложение векторов по правилу треугольника.
. Переставьте слагаемые местами и проследите по чертежу, как чётко в этих ситуациях работает старое доброе сложение векторов по правилу треугольника.
Рассмотренное разложение вида 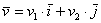 иногда называют разложением вектора в системе орт (т.е. в системе единичных векторов). Но это не единственный способ записи вектора, распространён следующий вариант:
иногда называют разложением вектора в системе орт (т.е. в системе единичных векторов). Но это не единственный способ записи вектора, распространён следующий вариант:
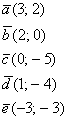 Или со знаком равенства:
Или со знаком равенства: 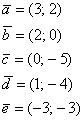
Сами базисные векторы записываются так:  и
и 
То есть, в круглых скобках указываются координаты вектора. В практических задачах используются все три варианта записи.
Сомневался, говорить ли, но всё-таки скажу: координаты векторов переставлять нельзя. Строго на первом месте записываем координату, которая соответствует единичному вектору 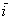 , строго на втором месте записываем координату, которая соответствует единичному вектору
, строго на втором месте записываем координату, которая соответствует единичному вектору 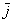 . Действительно,
. Действительно, 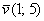 и
и 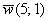 – это ведь два разных вектора.
– это ведь два разных вектора.
С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для простоты отложу от начала координат:
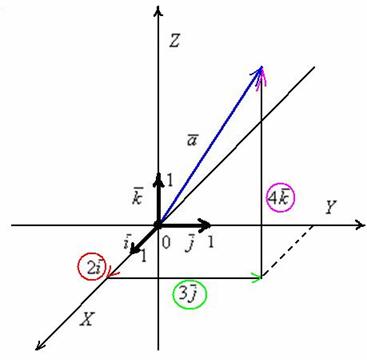
Перед вами ортонормированный базис  трехмерного пространства и прямоугольная система координат, единичные векторы
трехмерного пространства и прямоугольная система координат, единичные векторы  данного базиса попарно ортогональны:
данного базиса попарно ортогональны:  и
и 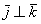 . Ось
. Ось 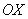 наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. О том, как правильно выполнять плоские и трехмерные чертежи на клетчатой бумаге, читайте в самом начале методички Графики и свойства функций.
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. О том, как правильно выполнять плоские и трехмерные чертежи на клетчатой бумаге, читайте в самом начале методички Графики и свойства функций.
Любой вектор 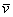 трехмерного пространства можно единственным способом разложить по ортонормированному базису
трехмерного пространства можно единственным способом разложить по ортонормированному базису 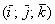 :
:
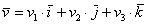 , где
, где 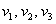 – координаты вектора
– координаты вектора 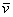 (числа) в данном базисе.
(числа) в данном базисе.
Пример с картинки: 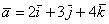 . Давайте посмотрим, как здесь работают правила действий с векторами. Во-первых, умножение вектора на число:
. Давайте посмотрим, как здесь работают правила действий с векторами. Во-первых, умножение вектора на число: 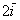 (красная стрелка),
(красная стрелка), 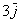 (зеленая стрелка) и
(зеленая стрелка) и 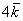 (малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх, векторов:
(малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх, векторов: 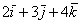 . Вектор суммы
. Вектор суммы 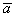 начинается в исходной точке отправления (начало вектора
начинается в исходной точке отправления (начало вектора 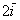 ) и утыкается в итоговую точку прибытия (конец вектора
) и утыкается в итоговую точку прибытия (конец вектора 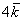 ).
).
Все векторы трехмерного пространства, естественно, тоже свободны, попробуйте мысленно отложить вектор 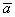 от любой другой точки, и вы поймёте, что его разложение
от любой другой точки, и вы поймёте, что его разложение 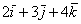 «останется при нём».
«останется при нём».
Аналогично плоскому случаю, помимо записи 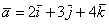 широко используются версии со скобками:
широко используются версии со скобками: 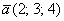 либо
либо 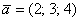 .
.
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор 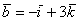 (дотошно
(дотошно 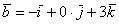 ) – запишем
) – запишем 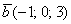 ;
;
вектор 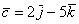 (дотошно
(дотошно 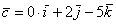 ) – запишем
) – запишем 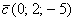 ;
;
вектор 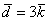 (дотошно
(дотошно 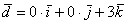 ) – запишем
) – запишем 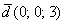 .
.
Базисные векторы записываются следующим образом:
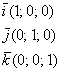
Вот, пожалуй, и все минимальные теоретические знания, необходимые для решения задач аналитической геометрии. Возможно многовато терминов и определений, поэтому чайникам рекомендую перечитать и осмыслить данную информацию ещё раз. Да и любому читателю будет полезно время от времени обращаться к базовому уроку для лучшего усвоения материала. Коллинеарность, ортогональность, ортонормированный базис, разложение вектора – эти и другие понятия будут часто использоваться в дальнейшем. Отмечу, что материалов сайта недостаточно для сдачи теоретического зачета, коллоквиума по геометрии, так как все теоремы (к тому же без доказательств) я аккуратно шифрую – в ущерб научному стилю изложения, но плюсом к вашему пониманию предмета. Для получения обстоятельной теоретической справки прошу следовать на поклон к профессору Атанасяну.
А мы переходим к практической части:
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть, даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
Как найти вектор по двум точкам?
Если даны две точки плоскости 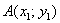 и
и 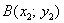 , то вектор
, то вектор 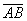 имеет следующие координаты:
имеет следующие координаты:
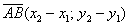
Если даны две точки пространства 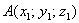 и
и 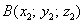 , то вектор
, то вектор 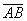 имеет следующие координаты:
имеет следующие координаты:
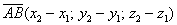
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора 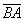 . Формулы в конце урока.
. Формулы в конце урока.
Даны две точки плоскости 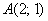 и
и 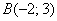 . Найти координаты вектора
. Найти координаты вектора 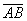
Решение: по соответствующей формуле:
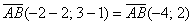
Как вариант, можно было использовать следующую запись:
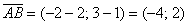
Эстеты решат и так: 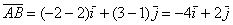
Лично я привык к первой версии записи.
Ответ: 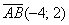
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
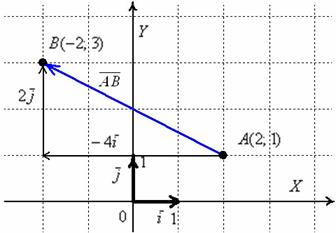
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 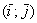 , в данном случае
, в данном случае 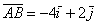 . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости  .
.
Записи координат точек и координат векторов вроде бы схожи: 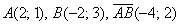 , а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
, а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
а) Даны точки 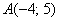 и
и 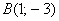 . Найти векторы
. Найти векторы 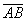 и
и 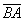 .
.
б) Даны точки 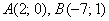 и
и 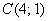 . Найти векторы
. Найти векторы 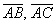 и
и 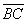 .
.
в) Даны точки 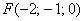 и
и 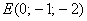 . Найти векторы
. Найти векторы 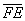 и
и 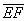 .
.
г) Даны точки 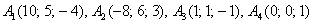 . Найти векторы
. Найти векторы 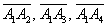 .
.
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости 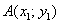 и
и 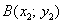 , то длину отрезка
, то длину отрезка 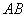 можно вычислить по формуле
можно вычислить по формуле 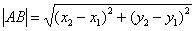
Если даны две точки пространства 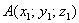 и
и 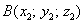 , то длину отрезка
, то длину отрезка 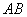 можно вычислить по формуле
можно вычислить по формуле 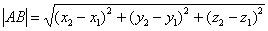
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: 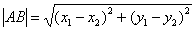 и
и 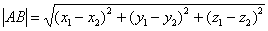 , но более стандартен первый вариант
, но более стандартен первый вариант
Даны точки 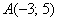 и
и 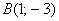 . Найти длину отрезка
. Найти длину отрезка 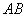 .
.
Решение: по соответствующей формуле:
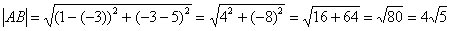
Ответ: 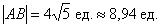
Для наглядности выполню чертёж
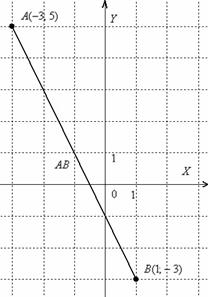
Отрезок 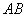 – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ
– это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ 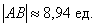 можно проверить обычной линейкой, непосредственно измерив длину отрезка.
можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат 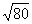 и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так:
и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: 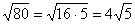 . Конечно, оставить ответ в виде
. Конечно, оставить ответ в виде 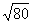 не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
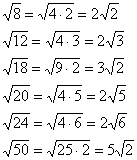
Нередко под корнем получается достаточно большое число, например 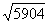 . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:
. Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: 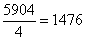 . Да, разделилось нацело, таким образом:
. Да, разделилось нацело, таким образом: 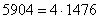 . А может быть, число
. А может быть, число 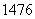 ещё раз удастся разделить на 4?
ещё раз удастся разделить на 4? 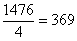 . Таким образом:
. Таким образом: 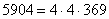 . У числа
. У числа 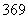 последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять:
последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: 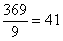 . В результате:
. В результате:
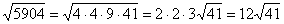 Готово.
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
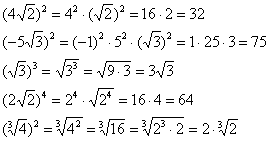
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Даны точки 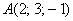 и
и 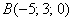 . Найти длину отрезка
. Найти длину отрезка 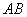 .
.
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости 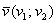 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле 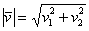 .
.
Если дан вектор пространства 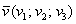 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле 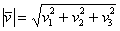 .
.
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Даны точки 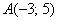 и
и 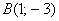 . Найти длину вектора
. Найти длину вектора 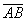 .
.
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор 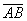 :
:
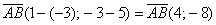
По формуле 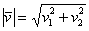 вычислим длину вектора:
вычислим длину вектора:
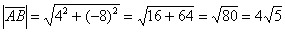
Ответ: 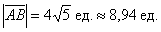
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой.
Выполним чертеж к задаче:
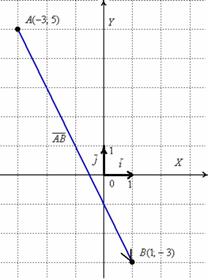
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка  равна длине вектора
равна длине вектора  . Так же очевидно, что длина вектора
. Так же очевидно, что длина вектора  будет такой же. По итогу:
будет такой же. По итогу: 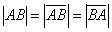
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки 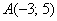 и
и 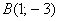 . Найти длину отрезка
. Найти длину отрезка 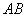 .
.
Вместо применения формулы 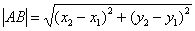 , поступаем так:
, поступаем так:
1) Находим вектор 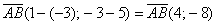 .
.
2) А теперь ссылаемся на то, что длина отрезка 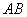 равна длине вектора
равна длине вектора 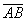 :
:
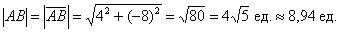
Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
а) Даны точки 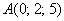 и
и 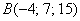 . Найти длину вектора
. Найти длину вектора 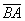 .
.
б) Даны векторы 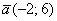 ,
, 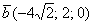 ,
, 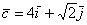 и
и 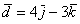 . Найти их длины.
. Найти их длины.
Решения и ответы в конце урока.
Действия с векторами в координатах
В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов:
1) Правило сложения векторов. Рассмотрим два вектора плоскости 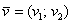 и
и 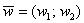 . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты: 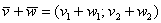 . Как просто. На всякий случай запишу частный случай – формулу разности векторов:
. Как просто. На всякий случай запишу частный случай – формулу разности векторов: 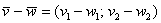 . Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор
. Аналогичное правило справедливо для суммы любого количества векторов, добавим например, вектор 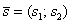 и найдём сумму трёх векторов:
и найдём сумму трёх векторов: 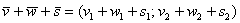
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 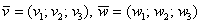 , то их суммой является вектор
, то их суммой является вектор 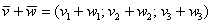 .
.
2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор 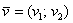 умножить на число
умножить на число 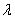 , необходимо каждую координату данного вектора умножить на число
, необходимо каждую координату данного вектора умножить на число 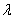 :
:
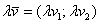 .
.
Для пространственного вектора 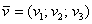 правило такое же:
правило такое же:
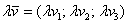
Приведённые факты строго доказываются в курсе аналитической геометрии.
Примечание: Данные правила справедливы не только для ортонормированных базисов 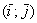 ,
, 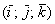 но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов.
но и для произвольного аффинного базиса плоскости или пространства. Более подробно о базисах читайте в статье Линейная (не) зависимость векторов. Базис векторов.
Даны векторы 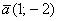 и
и 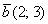 . Найти
. Найти 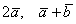 и
и 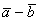
Решение чисто аналитическое:
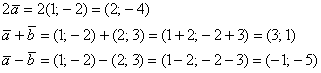
Ответ: 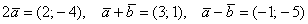
Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать, что векторы заданы в ортонормированном базисе  , то графическое решение задачи будет таким:
, то графическое решение задачи будет таким:
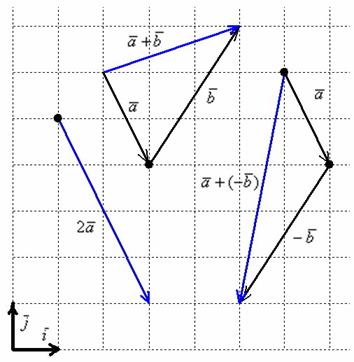
Коль скоро речь идет только о векторах в ортонормированном базисе, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну, и координатную сетку для удобства. Строго говоря, ранее я допустил небольшой огрех – в некоторых чертежах урока тоже можно было не чертить декартову прямоугольную систему координат. Векторам она не нужна, им нужен базис. Впрочем, лучше всегда рисуйте, а то напугаете всех своими знаниями =)
Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости.
Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо):
Даны векторы 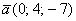 и
и 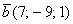 . Найти
. Найти 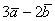 и
и 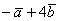
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
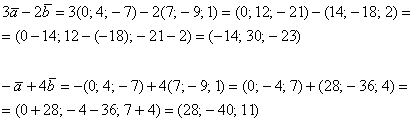
Ответ: 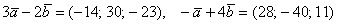
И в заключение занятный пример с векторами на плоскости:
Даны векторы 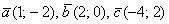 . Найти
. Найти 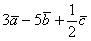 и
и 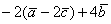
Это задача для самостоятельного решения.
Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки:
Это, так скажем, вектор-минимум студента =)
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Задание: 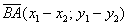 ,
, 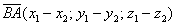
Пример 2: Решение:
а)
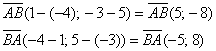
б)
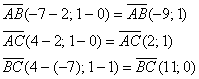
в)
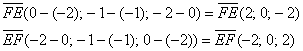
г)
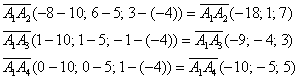
Пример 4: Решение:
По соответствующей формуле: 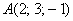 и
и 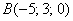
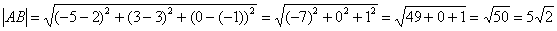
Ответ: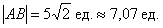
Пример 6: 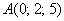 и
и 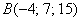
а) Решение: найдём вектор 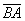 :
:
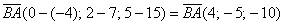
Вычислим длину вектора:
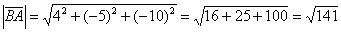
Ответ: 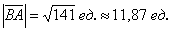
б) Решение:
Вычислим длины векторов:
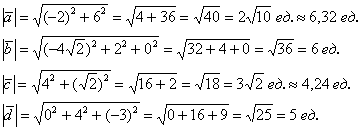
Пример 9: Решение:
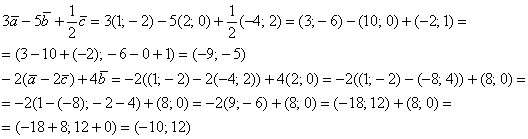
Примечание: Перед выполнением действий можно предварительно раскрыть скобки:
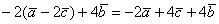
Ответ: 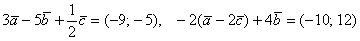
Автор: Емелин Александр
(Переход на главную страницу)
 Качественные работы без плагиата – Zaochnik.com
Качественные работы без плагиата – Zaochnik.com
mathprofi.ru
