Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Закон сложения скоростей

Кинематика — это просто!

Если тело движется относительно системы отсчета К₁ со скоростью V₁,
а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V,
то скорость тела (V₂) относительно второй системы отсчета К₂
равна геометрической сумме векторов V₁ и V.

Упрощаем форммулировку, не меняя смысла:

где всегда
К₂ — неподвижная система отсчета
V₂ — скорость тела относительно неподвижной системы отсчета (К₂)

V — скорость подвижной системы отсчета (К₁) относительно неподвижной системы отсчета (К₂)

Алгоритм решения задачи на закон сложения скоростей

1. Определить тело — обычно это тело, о скорости которого спрашивается в задаче.
2. Выбрать неподвижную систему отсчета (дорога, берег) и подвижную систему отсчета (обычно это второе движущееся тело).

3. Ввести обозначения скоростей (V₁, V₂, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.

Пример решения простейшей задачи на закон сложения скоростей

Задача

Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.

Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

1. В задаче спрашивается о скорости первого автомобиля — значит тело — первый автомобиль.
2. По условию задачи выбираем:
K₁ — подвижная система отсчета сязана со вторым автомобилем
К₂ — неподвижная система отсчета связана с дорогой

3. Вводим обозначения скоростей:
V₁ — скорость тела (первого авто) относительно подвижной системы отсчета (второго авто) — найти!
V₂ — скорость тела (первого авто) относительно неподвижной систеы отсчета (дороги) — дано 10м/с
V — скоростьь подвижной системы отсчета (второго авто) относительно неподвижной системы отсчета (дороги) — дано 20двух уравнений:м/с

Теперь понятно, что в задаче надо определить V₁.
4. Делаем чертеж, выписываем формулу:

5. далее по алгоритму .

class-fizika.ru

СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН

— определяет связь между значениямискорости материальной точки по отношению к разл. системам отсчёта, движущимсядруг относительно друга. В нерелятивистской физике, когда рассматриваютсяскорости, малые по сравнению со скоростью света с, справедлив законсложения скоростей Галилея:

где u и u’ — скорости частицы в двух инерциалъных системах отсчётаК т К’ соответственно (система К’ движется относительно . со скоростью v). Если скорости движения близки к е, то ф-ла(1) неприменима и справедлив С. с. з. частной (специальной) относительноститеории:

где и — проекции скорости частицы в системе отсчёта К(К’ )на направления параллельное и перпендикулярное к v.В пределе и ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде

Из ф-лы (3), в частности, следует, что если и = с, то и и’= с независимо от в, т. е. абс. величина скорости света не зависитот движения системы отсчёта. Тот же вывод справедлив, разумеется, и припроизвольном направлении скоростей, когда надо пользоваться ф-лой (2).

В случае неравномерных относит. движений двух систем отсчёта, а такжепри наличии тяготения (т. е. в случае общей теории относительности)все приведённые соотношения справедливы в локально сопутствующих инерциальныхсистемах отсчёта , т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК’ соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Смотреть что такое «СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН» в других словарях:

Закон — 1) необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения скоростей … Политология. Словарь.

ЗАКОН — необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения скоростей в… … Большой Энциклопедический словарь

ЗАКОН (в науке) — ЗАКОН, необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности. Существуют три основные группы законов: специфические, или частные (напр., закон сложения… … Энциклопедический словарь

закон — а; м. 1. Нормативный акт, постановление высшего органа государственной власти, принятый в установленном порядке и имеющий юридическую силу. Кодекс законов о труде. З. о социальном обеспечении. З. о воинской обязанности. З. о рынке ценных бумаг.… … Энциклопедический словарь

ЗАКОН — (филос., науч.), необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие 3. родственно понятию сущности. Существуют три осн. группы 3.: специфические, или частные (напр., 3. сложения скоростей… … Естествознание. Энциклопедический словарь

Параллелограмм скоростей — геометрическое построение, выражающее закон сложения скоростей. Правило П. с. состоит в том, что при сложном движении (см. Относительное движение) абсолютная скорость точки представляется как диагональ параллелограмма, построенного на… … Большая советская энциклопедия

ПРОСТРАНСТВО И ВРЕМЯ — категории, обозначающие осн. формы существования материи. Пр во (П.) выражает порядок сосуществования отд. объектов, время (В.) порядок смены явлений. П. и в. осн. понятия всех разделов физики. Они играют гл. роль на эмпирич. уровне физ. познания … Физическая энциклопедия

АБЕРРАЦИЯ СВЕТА — в астрономии, изменение видимого положения светила на небесной сфере, обусловленное конечностью скорости света и движением наблюдателя вследствие вращения Земли (суточная А. с.), обращения Земли вокруг Солнца (годичная А. с.) и перемещения Солн.… … Физическая энциклопедия

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — физическая теория, рассматривающая пространственно временные закономерности, справедливые для любых физ. процессов. Универсальность пространственно временных св в, рассматриваемых О. т., позволяет говорить о них просто как о .св вах пространства… … Физическая энциклопедия

Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор … Википедия

dic.academic.ru

Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Закон сложения скоростей

Формулировка закона:

Как в учебнике Буховцева для 10 класса:

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.

Вторая формулировка запоминается проще, какой ползоваться решайте сами!

К₁ — подвижная система отсчета
V₁ — скорость тела относительно подвижной системы отсчета (К₁)

Алгоритм решения задачи на закон сложения скоростей

Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)

3. Ввести обозначения скоростей (V₁, V₂, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.

Пример решения простейшей задачи на закон сложения скоростей

Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.

Решение:

3. Вводим обозначения скоростей:
V₁ — скорость тела (первого авто) относительно подвижной системы отсчета (второго авто) — найти!
V₂ — скорость тела (первого авто) относительно неподвижной систеы отсчета (дороги) — дано 10м/с
V — скоростьь подвижной системы отсчета (второго авто) относительно неподвижной системы отсчета (дороги) — дано 20двух уравнений:м/с

5. далее по алгоритму .

§ 10. Закон сложения скоростей

Преобразования Лоренца дают нам возможность вычислять изменение координат события при переходе от одной системы отсчета к другой. Поставим теперь вопрос о том, как при изменении системы отсчета будет меняться скорость одного и того же тела?

В классической механике, как известно, скорость тела просто складывается со скоростью системы отсчета. Сейчас мы убедимся, что в теории относительности скорость преобразуется по более сложному закону.

Мы снова ограничимся рассмотрением одномерного случая. Пусть две системы отсчета S и S` «наблюдают» за движением некоторого тела, которое перемещается равномерно и прямолинейно параллельно осям х и х` обеих систем отсчета. Пусть скорость тела, измеренная системой отсчета S, есть и; скорость того же тела, измеренную системой S`, обозначим через и` . Буквой v будем по-прежнему обозначать скорость системы S` относительно S.

Допустим, что с нашим телом происходят два события, координаты которых в системе S суть x₁,t₁, и х₂, t₂. Координаты тех же событий в системе S` пусть будут х`₁, t`<sub>1</sub>; x`₂, t`₂. Но скорость тела есть отнощение пройденного телом пути к соответствующему промежутку времени; поэтому, чтобы найти скорость тела в той и другой системах отсчета, нужно разность пространственных координат обоих событий разделить на разность временных координат

которую можно, как всегда, получить из релятивистской, если скорость света считать бесконечной. Ту же формулу можно записать в виде

Для небольших, «обычных» скоростей обе формулы— релятивистская и классическая — дают практически совпадающие результаты, в чем читатель при желании легко сможет убедиться. Но при скоростях, близких к скорости света, разница становится весьма ощутимой. Так, если v=150 000 км/сек, u`=200 000 км/сек, то вместо классического результата u = 350 000 км/сек релятивистская формула дает u = 262 500 км/сек. Согласно смыслу формулы сложения скоростей, этот результат означает следующее.

Пусть система отсчета S` движется относительно системы отсчета S со скоростью v = 150 000 км/сек. Пусть в том же направлении движется тело, причем измерение его скорости системой отсчета S` дает результат u =200 000 км/сек. Если теперь измерить скорость того же тела с помощью системы отсчета S то получится u=262 500 км/сек.


Следует подчеркнуть, что полученная нами формула предназначена именно для пересчета величины скорости одного и того же тела от одной системы отсчета к другой, а отнюдь не для вычисления «скорости сближения» или «удаления» двух тел. Если мы из одной и той же системы отсчета наблюдаем два движущихся навстречу друг другу тела, причем скорость одного тела равна 150 000 км/сек, а второго — 200 000 км/сек, то расстояние между этими телами каждую секунду будет уменьшаться на 350 000 км. Теория относительности не упраздняет законов арифметики.

Читатель уже понял, конечно, что, применяя эту формулу к скоростям, не превосходящим скорость света, мы снова получим скорость, не превосходящую с. Не представляет никакого труда доказать это утверждение вполне строго. Действительно, легко проверить.

Пусть система отсчета S` движется относительно системы отсчета S со скоростью v = 150 000 км/сек. Пусть в том же направлении движется тело, причем измерение его скорости системой отсчета S` дает результат u` =200 000 км/сек. Если теперь измерить скорость того же тела с помощью системы отсчета S то получится u=262 500 км/сек.


Следует подчеркнуть, что полученная нами формула предназначена именно для пересчета величины скорости одного и того же тела от одной системы отсчета к другой, а отнюдь не для вычисления «скорости сближения» или «удаления» двух тел. Если мы из одной и той же системы отсчета наблюдаем два движущихся навстречу друг другу тела, причем скорость одного тела равна 150 000 км/сек, а второго — 200 000 км/сек, то расстояние между этими телами каждую секунду будет уменьшаться на 350 000 км. Теория относительности не упраздняет законов арифметики.

Читатель уже понял, конечно, что, применяя эту формулу к скоростям, не превосходящим скорость света, мы снова получим скорость, не превосходящую с. Не представляет никакого труда доказать это утверждение вполне строго. Действительно, легко проверить, что имеет место равенство

Так как и` ≤ с и v 2 /c 2 )
Мы получим тангенс угла наклона луча к оси z`, если разделим и`<sub>х</sub> на и`_z:
tg α = и`<sub>х</sub> / и`_z = (v/c) / √(1 — v 2 /c 2 )

Если скорость v не очень велика, то можно применить известную нам приближенную формулу, с помощью которой получаем
tg α = v/c + 1/2*v 2 /c 2 .
Первое слагаемое представляет собой хорошо известный классический результат; второе слагаемое есть релятивистская поправка.

Орбитальная скорость Земли равна примерно 30 км/сек, так что (v/c) = 10 -4 . Для малых углов тангенс равен самому углу, измеренному в радианах; так как радиан содержит круглым счетом 200 000 угловых секунд, то получаем для угла аберрации:
α = 20°
Релятивистская поправка в 20 000 000 раз меньше и лежит далеко за пределами точности астрономических измерений. Вследствие аберрации звезды описывают ежегодно на небе эллипсы с большой полуосью в 20″.

Когда мы смотрим на движущееся тело, мы видим его не там, где оно находится в данный момент, а там, где оно было несколько раньше, ибо свету нужно некоторое время, чтобы Дойти от тела до наших глаз. Это явление с точки зрения теории относительности эквивалентно аберрации и сводится к ней при переходе к той системе отсчета, в которой рассматриваемое тело неподвижно. На основании этого простого соображения мы можем получить формулу аберрации совершенно элементарным путем, не прибегая к релятивистскому закону сложения скоростей.

Пусть наше светило движется параллельно земной поверхности справа налево (рис. 22). Когда оно прибывает в точку А, наблюдатель, находящийся точно под ним в точке С, видит его еще в точке В. Если скорость светила равна v, а промежуток времени, в течение которого оно проходит отрезок АВ, равен Δt, то

AB = Δt,
BC=cΔt,

sin α = AB/BC = v/c.

Но тогда, согласно формуле тригонометрии,

что и требовалось доказать. Заметим, что в классической кинематике эти две точки зрения не эквивалентны.

Интересен также следующий вопрос. Как известно, в классической кинематике скорости складываются по правилу параллелограмма. Мы заменили этот закон другим, более сложным. Значит ли это, что в теории относительности скорость уже не есть вектор?

Во-первых, то обстоятельство, что u ≠ u`+v (жирными буквами мы обозначаем векторы), само по себе не дает еще оснований отрицать векторную природу скорости. Из двух данных векторов третий вектор можно получить не только путем их сложения, а, например, путем векторного умножения, и вообще бесчисленным множеством способов. Ниоткуда не следует, что при перемене системы отсчета векторы и` и v обязаны именно складываться. И действительно, существует формула, выражающая и через и` и v с помощью операций векторного исчисления:

В связи с этим следует признать, что название «закон сложения скоростей» не совсем удачно; правильнее говорить, как это и делают некоторые авторы, не о сложении, а о преобразовании скорости при перемене системы отсчета.

Во-вторых, и в теории относительности можно указать случаи, когда скорости складываются по-прежнему векторно. Пусть, например, тело двигалось в течение некоторого промежутка времени Δt со скоростью u₁, а затем — такой же отрезок времени со скоростью u₂. Это сложное движение можно заменить движением с постоянной скоростью u = u₁+ u₂. Здесь скорости u₁ и u₂ складываются, как векторы, по правилу параллелограмма; теория относительности не вносит здесь никаких изменений.
Следует вообще заметить, что большинство «парадоксов» теории относительности связано так или иначе с изменением системы отсчета. Если рассматривать явления в одной и той же системе отсчета, то вносимые теорией относительности изменения в их закономерности далеко не столь кардинальны, как часто думают.

Отметим еще, что естественным обобщением обычных трехмерных векторов в теории относительности являются векторы четырехмерные; при перемене системы отсчета они преобразуются по формулам Лоренца. Кроме трех пространственных компонент, они имеют компоненту временную. В частности, можно рассматривать четырехмерный вектор скорости. Пространственная «часть» этого вектора, однако, не совпадает с обычной трехмерной скоростью, и вообще четырехмерная скорость по своим свойствам заметно отличается от трехмерной. В частности, сумма двух четырехмерных скоростей не будет уже, вообще говоря, скоростью.

Закон сложения скоростей в классической механике

Основная статья: Теорема о сложении скоростей

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

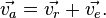
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

1. Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).

2. Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.

3. Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть 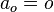, то ускорение 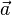тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см. второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-либо конкретной из инерциальных систем отсчета.

Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так:

Если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они накладывают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.

Центра масс системы материальных точек

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где 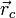— радиус-вектор центра масс, 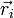— радиус-вектор i-й точки системы, — масса i-й точки.

Для случая непрерывного распределения масс:

где — суммарная масса системы, — объём, — плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами , то радиус-вектор центра масс такой системы 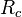связан с радиус-векторами центров масс тел соотношением:

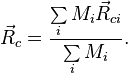
Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.

Закон движения центра масс

Теорема о движении центра масс (центра инерции) системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему.

Объектами, о которых идёт речь в теореме, могут, в частности, являться следующие :

Импульс материальной точки и системы тел — это физическая векторная величина, которая является мерой действия силы, и зависит от времени действия силы.

Закон сохранения импульса (доказательство)

Закон сохранения импульса (Закон сохранения количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородностью пространства.

Согласно второму закону Ньютона для системы из N частиц:

где импульс системы

а — равнодействующая всех сил, действующих на частицы системы

Здесь — равнодействующая сил, действующим на n-ю частицу со стороны m-ой, а — равнодействующая всех внешних сил, действующих k-ю частицу. Согласно третьему закону Ньютона, силы вида и 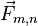будут равны по абсолютному значению и противоположны по направлению, то есть . Поэтому вторая сумма в правой части выражения (1) будет равна нулю, и получаем, что производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на систему:

Внутренние силы исключаются третьим законом Ньютона.

Для систем из N частиц, в которых сумма всех внешних сил равна нулю

или для систем, на частицы которых не действуют внешние силы 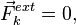(для всех k от 1 до n), имеем

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

(постоянный вектор).

То есть суммарный импульс системы из N частиц, где N любое целое число, есть величина постоянная. Для N = 1 получаем выражение для одной частицы.

Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, но и для систем, сумма всех внешних сил равна нулю. Равенство нулю всех внешних сил достаточно, но не необходимо для выполнения закона сохранения импульса.

Если проекция суммы внешних сил на какую-либо направление или координатную ось равна нулю, то в этом случае говорят о законе сохранения проекции импульса на данное направление или координатную ось.

Динамика вращательного движения твердого тела

Основной закон динамики МАТЕРИАЛЬНОЙ ТОЧКИ при вращательном движении можно сформулировать следующим образом:

«Произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку: «M = I·e.

Основной закон динамики вращательного движения ТВЕРДОГО ТЕЛА относительно закрепленной точки можно сформулировать следующим образом:

«Произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси (z), вокруг которой происходит вращение: «

Основные понятия: момент силы, момент инерции, момент импульса

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массывращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется.

Не нашли то, что искали? Воспользуйтесь поиском:

webcache.googleusercontent.com