Закон сохранения момента силы

Оглавление:

Электронная библиотека

Моментом импульса материальной точки относительно неподвижной точки ( ) называется физическая величина, определяемая векторным произведением:

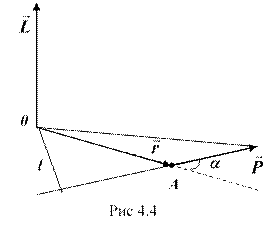где -радиус-вектор, проведенный из точки О в точку А; — импульс материальной точки (рис. 4.4); – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль вектора момента импульса равен:

где – угол между векторами и ; – плечо вектора относительно точки O.

Моментом импульса относительно неподвижной оси (z) называется скалярная величина ( ), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса ( ) не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, то есть радиус является плечом вектора . Поэтому можем записать, что момент импульса отдельной частицы равен: и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцировав уравнение (4.1) по времени получим:

Это выражение есть еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Физический смысл этого выражения: скорость изменения момента импульса равна моменту сил.

В векторной форме это можно записать так:

В замкнутой системе момент ( ) внешних сил равен нулю и, следовательно, , откуда

Выражение (4.2) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется с течением времени. Закон сохранения момента импульса – фундаментальный закон природы.

libraryno.ru

Закон сохранения момента силы

В общем случае движение твердого тела можно представить в виде суммы двух движений — поступательного со скоростью ис и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. Тогда полная кинетическая энергия этого тела.

Здесь Jc — момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.

1.7.5. Закон сохранения момента импульса

Для замкнутой системы тел момент внешних сил М всегда равен нулю, т. к. внешние силы вообще не действуют на замкнутую систему.

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

Это один из фундаментальных законов природы.

Аналогично для замкнутой системы тел, вращающихся вокруг оси z.

Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.

Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.

Закон сохранения момента импульса является прямым следствием законов Ньютона и изотропности пространства — эквивалентности свойств пространства в различных направлениях.

Существует множество различных задач, связанных с вращающимися системами, в которых скорости вращения или моменты импульса можно вычислить с помощью закона сохранения момента импульса.

Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом — быстро вращающимся телом, имеющим три степени свободы.

Гироскоп на кардановом подвесе (как это изображено на рис. 1.7.11) не испытывает действия момента в результате вращения Земли или в результате движения самолета, на котором он укреплен. Поэтому

www.chem-astu.ru

Закон сохранения момента импульса системы материальных точек Момент силы и импульса относительно точки и оси. — презентация

Презентация была опубликована 4 года назад пользователемГлеб Ятнов

Презентация на тему: » Закон сохранения момента импульса системы материальных точек Момент силы и импульса относительно точки и оси.» — Транскрипт:

1 Закон сохранения момента импульса системы материальных точек Момент силы и импульса относительно точки и оси

2 Статика – инженерная наука, изучающая равновесие твердых тел, находящихся под действием сил. Она необходима для определения максимально допустимых нагрузок. Чтобы удержать тело в покое (равновесии), необходимо выполнение 2-х условий: 1.Векторная сумма всех сил равна 0 2. Векторная сумма всех моментов сил равна 0

3 Момент силы F относительно неподвижной точки 0 – физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки 0 в точку приложения силы, на силу F.

4 Момент силы относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора М относительно произвольной точки данной оси. Значение М z не зависит от выбора положения точки 0 на оси z.

5 Момент импульса (количества движения) материальной точки относительно неподвижной точки 0 – физическая величина, определяемая векторным произведением

6 Момент импульса относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора L относительно произвольной точки данной оси. Для движения по окружности:

7 Уравнение моментов Математическая справка:

8 Производная по времени от момента импульса относительно точки равна моменту силы относительно этой точки. Производная по времени от момента импульса относительно оси равна моменту силы относительно этой оси.

9 Закон сохранения момента импульса системы материальных точек При произвольном движении системы n материальных точек:

10 Результирующий момент внутренних сил в соответствии с третьим законом Ньютона равен нулю.

11 В уравнении (1) операции дифференцирования и суммирования можно поменять местами: Если внешние силы на систему не действуют, то Момент импульса замкнутой системы величина постоянная, т.е. с течением времени не меняется – закон сохранения момента импульса.

12 Закон сохранения момента импульса является прямым следствием законов Ньютона и изотропности пространства – эквивалентности свойств пространства в различных направлениях. Во многих задачах, связанных с вращающимися системами, угловая скорость вращения ω и момент импульса можно вычислить с помощью закона сохранения момента импульса.

13 Пример: скамья Жуковского, человек на вращающейся скамье держит в руках пару гантелей. Пусть масса двух гантелей m и R 1 таковы, что в первоначальный момент времени момент импульса человека L ч1 равен моменту импульса гантелей L г1 : L ч1 = L г1 (1). Вращается с угловой скоростью ω 1. Затем сжимает руки и прижимает гантели к себе:

14 Начальный момент импульса системы: Во втором случае: Т.к. L ч1 = L г1 По закону сохранения момента импульса (уравнение (3) равно (5)):

15 Уравнение (7) делим на (8): Уравнение (9) подставляем в (6): Уравнение (4) подставляем в (10):

16 Аналогичная ситуация возникает, когда фигурист прижимает руки к себе и начинает вращаться быстрее.

17 Гироскоп Гироскоп – быстро вращающееся симметричное твердое тело, ось вращения которого может изменять свое направление в пространстве. Происходит от греческого

18 Свойства гироскопа проявляются у вращающихся небесных тел, снаряда (пули), роторов турбин, установленных на судах, волчка, юлы. На свойствах гироскопа основаны различные приборы и устройства, применяемые в технике. Свойства гироскопа проявляются при выполнении двух условий: 1. ось вращения гироскопа должна иметь возможность изменять своё положение в пространстве; 2. частота вращения гироскопа вокруг своей оси должна быть много больше скорости изменения направления оси в пространстве.

19 Для того чтобы ось гироскопа могла свободно поворачиваться в пространстве, его обычно закрепляют на кольцах, так называемая карданова подвеса. Дискообразное тело – гироскоп закреплено на оси аа 1 – ось гироскопа, которая может вращаться вокруг перпендикулярной ей горизонтальной оси bb 1, которая, в свою очередь, может поворачиваться вокруг вертикальной оси dd 1. Все три оси пересекаются в одной точке, называемой центром подвеса. Такой гироскоп имеет 3 степени свободы и может совершать любой поворот около центра подвеса. Силами трения в подшипниках и моментами импульса колец пренебрегаем.

20 Пока гироскоп неподвижен, его можно ориентировать в пространстве любым образом. Если гироскоп начинает вращаться с большой угловой скоростью ω, то при отсутствии внешних сил (F внеш =0) М = 0 и т.е. ось гироскопа сохраняет свое положение в пространстве.

21 Если к оси гироскопа y приложить пару сил F, то возникает вращающий момент М. Ось гироскопа поворачивается вокруг оси z, а не вокруг х, как это могло показаться. Это гироскопический эффект.

22 За время dt гироскоп получит приращение dL и станет Вектор L совпадает с направлением оси вращения гироскопа. Если время воздействия мало dt 0, то даже если момент сил М велик, dL 0, т.е. кратковременное действие сил не приводит к изменению ориентации оси гироскопа, она будет сохранять определённое направление в пространстве.

23 Гироскоп Применение: — навигационные устройства (гирокомпас, гирогоризонт), — поддержание заданного направления движения (автопилот). При конструировании судов и самолетов необходимо учитывать гироскопические силы, возникающие в подшипниках массивных валов двигателей, роторов турбин, гребных валов и т.п.

24 Динамика вращательного движения абсолютно твёрдого тела относительно неподвижной оси Основное уравнение динамики вращательного движения

25 При вращении абсолютно твёрдого тела вокруг неподвижной оси z каждая отдельная точка движется по окружности постоянного радиуса R i с некоторой скоростью v i. Моменты силы: Закон сохранения момента импульса:

26 Момент импульса относительно точки 0 для i точки твёрдого тела: Проекция на ось z относительно точки 0:

28 Твёрдое тело – система жёстко связанных материальных точек. Следовательно, для твёрдого тела: — момент инерции материальной точки относительно оси z. — момент инерции твердого тела относительно оси z. — момент импульса (количества движения) твердого тела относительно оси z.

29 Закон сохранения момента импульса: Т.к. координатную ось z приняли произвольно, индекс можно опустить. – основное уравнение динамики вращательного движения.

30 В общем случае: – ускорение вращения твердого тела относительно неподвижной оси прямо пропорционально моменту всех внешних сил относительно этой оси и обратно пропорционально моменту инерции твердого тела относительно этой оси. Физический смысл: Момент инерции относительно оси – мера инерции твердого тела при вращательном движении относительно оси.

31 Момент инерции. Теорема Гюйгенса-Штейнера Момент инерции системы тел – физическая величина равная сумме произведений m i на : В случае непрерывного распределения масс сумма сводится к интегралу:

32 Кольцо Диск, цилиндр Стержень Шар

33 Теорема Гюйгенса-Штейнера: момент инерции относительно произвольной оси равен моменту инерции относительно параллельной ей оси, проходящей через центр масс J 0, сложенному с произведением массы тела на квадрат расстояния между ними а 2.

34 Пример: расчет момента инерции сплошного цилиндра радиуса R, высотой h. Разобьем на полые цилиндры r, r + dr, dr0. dm – масса всего полого цилиндра.

36 Закон сохранения момента импульса АТТ относительно неподвижной оси В общем виде В замкнутой системе Фундаментальный закон, связан с симметрией пространства, его изотропностью, т.е. физические законы не зависят от выбора направления осей системы координат.

38 Кинетическая энергия при вращательном движении АТТ Т.к. имеется АТТ, следовательно, для всех m i ω = const.

39 Динамика вращательного движения. Работа и мощность при вращательном движении относительно неподвижной оси Основное уравнение динамики вращательного движения: Закон сохранения момента импульса: Кинетическая энергия при вращательном движении:

40 Работа при вращательном движении идёт на увеличение его кинетической энергии: Из (1) следует Уравнение (5) подставляем в (4):

42 Плоское движение твердого тела Плоское движение – движение, при котором все участки траектории любых двух точек твёрдого тела лежат в параллельных плоскостях. Кинетическая энергия складывается из энергии поступательного движения и энергии вращения. v c – скорость центра масс, J c – момент инерции относительно оси, проходящей через центр масс.

43 Поступательное движение Вращательное движение mJmJ

www.myshared.ru

Закон сохранения момента импульса

В замкнутой системе выполняется закон сохранения момента импульса.

Вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться. Физики привычно объясняют этот феномен тем, что такое вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения. Момент импульса вращающегося тела прямо пропорционален скорости вращения тела, его массе и линейной протяженности. Чем выше любая из этих величин, тем выше момент импульса. Если теперь допустить, что тело вращается не вокруг собственного центра массы, а вокруг некоего центра вращения, удаленного от него, оно всё равно будет обладать вращательным моментом импульса. В математическом представлении момент импульса L тела, вращающегося с угловой скоростью ω, равен L = Iω, где величина I, называемая моментом инерции, является аналогом инерционной массы в законе сохранения линейного импульса, и зависит она как от массы тела, так и от его конфигурации — то есть, от распределения массы внутри тела. В целом, чем дальше от оси вращения удалена основная масса тела, тем выше момент инерции.

Сохраняющейся или консервативной принято называть величину, которая не изменяется в результате рассматриваемого взаимодействия. В рамках закона сохранения момента импульса консервативной величиной как раз и является угловой момент вращения массы — он не изменяется в отсутствие приложенного момента силы или крутящего момента — проекции вектора силы на плоскость вращения, перпендикулярно радиусу вращения, помноженной на рычаг (расстояние до оси вращения). Самый расхожий пример закона сохранения момента импульса — фигуристка, выполняющая фигуру вращения с ускорением. Спортсменка входит во вращение достаточно медленно, широко раскинув руки и ноги, а затем, по мере того, как она собирает массу своего тела всё ближе к оси вращения, прижимая конечности всё ближе к туловищу, скорость вращения многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции I, тем выше угловая скорость ω и, как следствие, короче период вращения, обратно пропорциональный ей.

Следует отметить, однако, что не любая приложенная извне сила сказывается на моменте вращения. Предположим, вы поставили свой велосипед «на попа» (колесами вверх) и сильно раскрутили одно из его колес. Понятно, что, приложив тормозящую силу трения к любой окружности колеса (нажав на ручной тормоз, приложив руку к резине или вращающимся спицам), вы, тем самым, снизите угловую скорость его вращения. Однако, сколько бы вы ни старались, вы не остановите вращения колеса, пытаясь воздействовать на ось вращения. Иными словами, для изменения момента вращения необходима не просто сила, а момент силы — то есть, сила, приложенная по направлению, отличному от направления оси вращения, и на некотором удалении от нее. Поэтому закон сохранения момента вращения можно сформулировать и несколько иначе: момент вращения тела изменяется только в присутствии момента силы, направленной на его изменение.

И тут возникает важное дополнительное замечание. До сих пор мы говорили об изменении момента вращения в плане ускорения или замедления вращения, как такового, но при этом тело продолжало вращаться всё в той же плоскости, и ось вращения не изменяла своей ориентации в пространстве. Теперь предположим, что момент силы приложен в плоскости, которая отличается от плоскости, в которой вращается тело. Такое воздействие неизбежно приведет к изменению направления оси вращения. В отсутствие же внешних воздействий закон сохранения момента импульса подразумевает, что направление оси вращения остается неизменным. Этот принцип широко используется в так называемых гироскопических навигационных приборах. В их основе лежит массивное, быстро вращающееся колесо — гироскоп, — которое не изменяет своей ориентации в пространстве, благодаря чему прибор стабильно указывает заданное направление, вне зависимости от угла поворота субмарины, самолета или спутника, на котором он установлен. С технической точки зрения гироскоп представляет собой массивный диск на осевых подшипниках низкого трения, раскрученный с очень большой скоростью. Идеальный гироскоп — это диск бесконечной массы, вращающийся с бесконечной скоростью в идеальном вакууме. В таком случае закон сохранения момента импульса подскажет нам, что направление оси такого идеального гироскопа не отклонится от исходной ни на одну угловую секунду, и он вечно будет указывать нам на изначально заданную точку. Искусственные спутники Земли, как правило, оснащаются несколькими независимыми гироскопами, вращающимися в разных плоскостях, и бортовая электроника, сопоставляя данные нескольких гироскопических компасов и усредняя поправки на возможные отклонения их показаний, безошибочно определяет координаты и ориентацию спутника в околоземном пространстве.

elementy.ru

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Используя связь момента силы и момента импульса для системы м.т. относительно неподвижной оси (например, оси Z ), имеем . Если ось симметрии совпадает с осью вращения, то .

В случае замкнутой системы (внешние силы не действуют, а внутренние силы попарно компенсируют друг друга) последнее выражение приобретает простой вид:

Формула (5.23) выражает закон сохранения вектора момента импульса.

В замкнутой (изолированной) системе тел (м.т.) суммарный вектор момента импульса остается неизменным.

Начальное состояние системы скамья Жуковского+колесо — неподвижное. По закону сохранения момента импульса для этих тел . При неизменном моменте инерции системы возникновение и рост угловой скорости колеса приводит к появлению и росту противоположного момента импульса у скамьи с мальчиком.

В видеодемонстрации «Опыте 2 с колесом» изменение направления вращения колеса на противоположное приводит также к изменению момента импульса скамьм Жуковского также на противоположное. Учитывая связь момента импульса с моментом инерции, имеем

или .

Закон справедлив не только для вектора момента импульса относительно оси, но и относительно полюса.

Закон сохранения вектора момента импульса является фундаментальным .

Замечание 1: момент силы не зависит от того, вращается тело или нет вокруг оси, т.к. в состоянии покоя он уравновешен моментом других сил, действующих на это тело. Если момент сил равен нулю, то тело вращается с постоянной угловой скоростью, т.е. . Если момент инерции тела не равен нулю (I≠ 0), тогда равна нулю производная угловой скорости по времени: d w /dt = 0 . Отсюда следует, что угловая скорость есть величина постоянная w = сonst . Если момент инерции тела может изменяться вследствие изменения взаимного расположения отдельных его частей, то при М = 0, I =сonst. Это значит, что изменение момента инерции тела влечет за собой изменение угловой скорости вращения, а именно: с увеличением момента инерции I его угловая скорость w уменьшается и наоборот.

Справедливость закона сохранения вектора момента импульса неоднократно проверялась на ряде опытов. Например, опыт со скамьей Жуковского.

ЖУКОВСКИЙ Николай Егорович (1847-1921), русский ученый. Им сделаны крупные открытия в области механики, основоположник современной аэродинамики.

Хорошей наглядной иллюстрацией этого закона служит видеодемонстрация «Опыт с гантелями» на скамье Жуковского. Удаление или приближение гантелей к центру соответственно увеличивает или уменьшает момент инерции системы мальчик-кресло. Что по закон сохранения момента импульса уменьшает или соответственно увеличивает угловую скорость вращения кресла.

Замечание 2: закон сохранения вектора момента импульса связан с изотропностью пространства как одного из свойств симметрии пространства-времени.

Под изотропностью пространства понимается следующее. Если замкнутую систему тел повернуть в пространстве на некоторый угол (тела должны находиться в тех же условиях, что и до поворота), то это не отразится на ходе всех последующих явлений в этой системе. Используя изотропность пространства можно доказать закон сохранения вектора момента импульса.

Если система замкнута, то на нее не действуют внешние силы, а действуют только внутренние. Пусть — векторы моментов внутренних сил, действующих на м.т. системы относительно неподвижного полюса 0. Затем совершим поворот всей системы вокруг полюса на малый угол dφ , при этом направления скоростей всех м.т. должны повернуться на такой же малый угол без изменения их величины. В виду изотропности пространства момент всех внутренних сил работы не совершает. Отсюда следует, что скалярное произведение равно нулю: