Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Законы Рауля и Генри

Законы Рауля и Генри. Законы Рауля и Генри описывают поведение любых бесконечно разбавленных растворов. [c.62]

При умеренных и низких давлениях во многих случаях с достаточной степенью точности можно упростить выражения законов Рауля и Генри, заменив летучести давлениями, а именно [c.62]

Законы Рауля и Генри в общем случае описывают поведение любых бесконечно разбавленных растворов. Для произвольных давлений и температур эти законы выражаются следующим образом [c.238]

При умеренных и низких давлениях во многих случаях может быть проведено с удовлетворительной точностью упрощение вышеприведенных выражений законов Рауля и Генри путем замены летучестей давлениями, а именно [c.239]

Приведенные уравнения законов Рауля и Генри, кроме их большого теоретического значения, находят применение при исследовании систем, отличающихся малой растворимостью одного компонента в другом, например при определении растворимостей газов в жидкостях, некоторых твердых тел в жидкостях и т. п. [c.239]

Такие растворы не подчиняются законам Рауля и Генри. Существуют так называемые растворы второго рода которые идеальны относительно имеющихся в них ионов, но не являются идеальными по отношению к молекулярным составляющим [c.385]

Составы растворов (262). 5-7-2. Законы Рауля и Генри (262). 5-7-3 Растворимость (262). 5-7-4. Термические свойства [c.140]

При весьма малых концентрациях растворимость можно связать с изменением температуры парообразования или затвердевания. При таких концентрациях (когда применимы законы Рауля и Генри) изменение температуры кипения жидкого растворителя может быть определено из выражения [c.239]

Кг называется константой Генри. Константы Генри для некоторых газов представлены в табл. 8.1. В области, где выполняется закон Генри, константа Ki не равна давлению пара чистого вещества. Зависимость от мольной доли представлена на рис. 8.3. (Кроме того, там, где вьшолняется закон Генри, стандартный химический потенциал /х°, вообще говоря, не совпадает с химическим потенциалом чистого вещества.) Только для совершенного раствора вьшолняется равенство Ki = р при Xi бесконечно ра -бавленных растворо -., Длч произвольных давлений и темперагур (раствор бинарпы1 ) закон Рауля [c.262]

Экспериментальные исследования ПО казывают, что при ПО строении теории бесконечно разбавленных растворов наиболее целесообразно исходить из закона Генри, так как в разбавленных растворах легче обнаружить отклонения от закона Генр и, чем отклонения от закона Рауля. Следует отметить также, что при формулировке зако номериостей, которым подчиняется давление пара разбавленных растворов, мы не использовал и явное выражение для химического потенциала растворителя и растворенных веществ в разбавленном растворе. Как будет показано в гл. 3, анализ уравнения Гиббса—Дюгема (1.32) и применение закона Генри (2.45) (в сочетании с некоторыми другими утверждениями нетермодинамического характера) позволяют найти аналитические выражения для химических потенциалов веществ в предельно разбавленных растворах. [c.41]

Закон Вант-Гоффа, так же как и закон Рауля для давления пара растворителя (2.46), закон Генри для давления пара растворенного вещества (2.45), криоскопическая (2.68) и эбулиоскопическая (2.79) формулы представляют со- ой примеры предельных законов бесконечно разбавленных растворов. [c.50]

Полученные выше формулы для р.(,(в,р, п) и Ц в,р, п) в рамках уже чисто термодинамического подхода решают все задачи теории слабых растворов, определяют тепловой эффект расширения примеси, обосновывают формулу Вант-Гоффа для осмотического давления, закон Генри о соотношении концентраций примеси в двух несмешивающихся растворителях, закон Рауля о смешении точки фазового перехода, связанного с присутствием примеси и т.д. Саму величину р(в) можно рассчитать, располагая потенциалом взаимодействия частиц примеси и растворителя Фо (1 г ), или ограничиться ее упрошенной оценкой (см. 1, п. г)), использованной при микроскопическом обосновывании уравнения Ван дер Ваальса, которая, несмотря на ее откровенную модельность, показательна в том отношении, что связывает баланс усредненных сил притяжения и отталкивания со свойствами компонент, составляюших данных слабый раствор.. [c.400]

Как отмечалось, со.аержание газа в жидкости соответствует закону Генри лишь в равновесных условиях, поэтому из законов Генри и Рауля нельзя определить скорость удаления газов (кинетику процесса). Между тем от скорости десорбции зависит конечный эффект дегазации, т.е. степень приближения системы к равновесному состоянию. В общем виде скорость десорбции газа определяется по уравнению [c.184]

К этим условиям следует добавить также ур-пия, обеспечивающие баланс частиц (такие, как ур-иии химич. реакций или условия сохранения числа частиц в каждом компоненте при днпамич. равновесии неск. фа и т. д.). Таким путем получаются закон действующих масс (см. также Тер.подина.иическое равновесие), правило фаз Гиббса (см. Фааовне превращения), основные закономерности для разбавленных растворов (законы Вант—1 оффа, Рауля, Генри и т. д.), условия кристаллизации и т. п. [c.377]

Понятие П. д. применимо только к смеси идеальных газов, в реальных жо газовых смес.чх оперируют понятием летучести. Связь П. д. с общим давлением с.месн (нри давлениях, близких к атм.) дается Дальтона закоио.м Pl — PNi, где Pi — П. д. компонента г. Ni —. мольная долл. Р — общее давление. Отсюда следует, что общее давление газовой смеси равно сумме П. д. компонентов. Если смесь паров над жидким бесконечно разбавленным раствором подчиняется законам идеальных газов, то связь между П. д. растворителя и его концентрацией в растворе дается Рауля законом, связь жо можду П. д. растворенного веп(ества и его концентрацией в растворе — Генри законо.м. [c.596]

Смотреть страницы где упоминается термин Законы Рауля и Генри : [c.40] [c.231] [c.413] [c.95] [c.838] [c.236] Смотреть главы в:

mash-xxl.info

Справочник химика 21

Химия и химическая технология

Генри Рауля закон

Если же уравнение (1.47) соблюдается лишь в ограниченном интервале изменения концентраций то А», уже не равно Р , и смысл уравнения (1.47) сводится к установлению простой пропорциональности между парциальным давлением p компонента газовой смеси и его мольной долей в равновесном жидком растворе. В этом случае коэффициент представляет собой константу закона Генри. Если же паровая фаза системы не является смесью идеальных газов, но, так же как и жидкая, подчиняется правилу фугитивности (1.40), законы Рауля и Генри должны выражаться уже с помощью фугитивностей. В общем виде уравнение (1.47) запишется так [c.28]

Р1 =pl° Xi р =Р2 -Х2 Закон Рауля Закон Генри [c.64]

Отклонения от закона Рауля. Закон Генри 83 [c.397]

Идеальный раствор. подчиняется одновременно и закону Рауля, и закону Генри. В этом случае говорят, что он подчиняется объединенному закону Генри—Рауля. Это значит, что одновременно выполняются два уравнения (для любого компонента) /г = //л г и /г = /гх,-, что дает =/ . Тогда стандартные состояния для обоих компонентов совпадают. [c.95]

Для предельно разбавленных растворов оказываются справедливыми ряд простых зависимостей, которые получили название законов разбавленных растворов . Это — законы Генри и Рауля, закон осмотического давления Вант-Гоффа, закон распределения Нернста, закономерности понижения температуры замерзания (криоскопия) и повышения температуры кипения (эбулиоскопия) растворов. Все эти законы были установлены экспериментальным путем и уже после их открытия получили термодинамическую интерпретацию. [c.21]

Таким образом, для бесконечно разбавленного раствора фугитивность растворителя вычисляют ПО закону Рауля, а фугитивность растворенного вещества—по закону Генри. Оба закона справедливы для любого агрегатного состояния раствора. [c.250]

Для растворов при высоком разбавлении оказываются справедливыми некоторые простые зависимости, которые получили название законов разбавленных растворов. Это законы Генри и Рауля, закон осмотического давления Вант-Гоффа, закон распределения Нерн-ста, закономерности понижения температуры замерзания (криоскопия), повышения температуры кипения (эбулиоскопия) раст- [c.48]

Для проблем, обсуждаемых в нашей книге, наиболее важны законы Генри и Рауля. Закон Генри был установлен раньше, в начале прошлого века. Закон утверждает, что растворимость [c.49]

Частные случаи закона распределения — правила и законы, выражающие равновесное распределение в-ва в двухфазных системах. Напр., для расчета равновесия жидкости и пара пользуются законами Рауля и Генри, первым — для в-ва, находящегося в избытке, вторым — для в-ва, являющегося примесью (см. Генри закон, Рауля закон). Распределение растворенного в-ва между двумя несмешивающимися жидкостями при постоянной т-ре характеризуется тем, что отношение его концентраций в этих двух фазах сохраняется постоянным (закон Бертло — Нернста). Распределение примеси между жидкой и твердой кристаллич. фазой описы- [c.55]

Законы термодинамического равновесия определяют условия, при которых процесс переноса любой субстанции (массы, энергии, импульса) приходит к своему завершению. Состояние системы, при котором необратимый перенос субстанции отсутствует, называют равновесным. Равновесное состояние описывается такими законами, как законы Генри, Рауля и др. Знание условий равновесия позволяет решать очень важные для анализа и расчета химико-технологических процессов задачи — определение направления процесса переноса (из какой фазы в какую переходит субстанция) и границ его течения, расчет движущей силы процесса. [c.17]

Разбавленные растворы достаточно точно подчиняются законам меж-фазного равновесия Рауля и Генри. По закону Рауля в равновесном состоянии двухфазной системы парциальное давление пара — того компонента жидкой смеси над раствором пропорционально его мольной доле х в растворе [c.56]

Хотя на практике лишь считанные вещества ведут себя как идеальный газ, их поведение представляет интерес как предельный случай. Основные термодинамические характеристики идеальных газов представлены в табл. А.5, а табл. А.6 суммирует изменения их характеристик в некоторых обычных процессах. Другие предельные соотношения преимущественно для смесей, например законы Генри, Рауля и Льюиса — Рэндалла, используются в последующих главах. В табл. А.2 представлено несколько именных термодинамических уравнений. [c.118]

Закон Рауля, закон осмотического давления и другие законы, относящиеся к разбавленным (или идеальным) растворам, можно вывести из уравнения (13.8). Все эти законы термодинамически связаны с законом Генри, и они распространяются на ту же область концентраций, в которой действителен закон Генри. [c.414]

В соответствии с ур-нием Гиббса — Дюгема П. м. в. растворенного в-ва сильнее зависят от концентрации, чем П. м. в. р-рителя. Поэтому в области малых концентраций поведение растворенного в-ва сильнее отклоняется от законов идеальных разбавл. р-ров (напр., Генри закона) по сравнению с отклонением поведения 1)-рителя от законов идеальных р-ров (напр., Рауля закона). Вблизи критич. точки р-рителя концентрац. зависимость П. м. в. усложняется (см. Критические растворы). [c.424]

Основанная на законах Генри и законах Рауля — Вант-Гоффа, эта термодинамическая теория охватывает такие вопросы, как свойства смеси двух жадностей, растворимость газов, жидкостей и твердых тел. По существу теория суммировала уже известные положения Коновалова, Шредера, [c.23]

Итак, закон Рауля является следствием закона Генри, но закон Генри не является следствием закона Рауля. [c.154]

Для реальных растворов законы Рауля и Генри выдерживаются с тем большей точностью, чем сильнее они разбавлены, а различие между ними выражается в том, что закон Рауля относится к растворителю, а закон Генри — к растворенным компонентам, концентрация которых мала. Принято считать, что раствор содержит по крайней мере один компонент, мольная доля которого может приближаться к единице. Такой компонент обычно называют растворителем. [c.29]

Это возражение представляется нам совершенно необоснованным. Второй закон термодинамики можно рассматривать как непосредственное следствие молекулярно-кинетической природы материи. В тенденции растворенного вещества к диффузии в растворе эта молекулярно-кинетическая природа обнаруживается в самой простой ее форме. Осмотическое давление является непосредственным мерилом этой тенденции. Таким образом, с теоретической точки зрения осмотическое давление является наиболее характерным свойством раствора [Е — 5]. К сказанному Гиншельвудом можно было бы только добавить, что для тех, кто отказывается от использования наглядного представления о парциальных давлениях и об осмотическом давлении как их сумме (или как-либо ограничивает эти представления), законы Генри, Рауля и Вант-Гоффа должны выглядеть как соотношения неожиданные, почти таинственные. [c.258]

Следует отметить, что зависимость, найденная Генри, аналогична закону Рауля. В обоих случаях устанавливается пропорциональность между давлением вещества в газовой фазе и концентрацией этого вещества в растворе. Разница лишь в том, что Рауль рассматривает вещество, составляющее основную массу раствора, а Генри —вещество, составляющее очень малую долю массы раствора. [c.88]

Таким образом, в бесконечно разбавленном растворе летучесть растворителя вычисляется по закону Рауля, а летучесть растворенного вещества по закону Генри. Оба закона справедливы вне зависимости от агрегатного состояния раствора. [c.260]

Существует класс растворов, летучести компонентов которых выражаются законом Рауля во всей области концентраций. В этом случае закон Генри тождествен закону Рауля, и коэффициент Генри равен летучести соответствующего чистого компонента при давлении, равном общему давлению над раствором. Такие растворы получили название идеальных, или совершенных, растворов. [c.60]

Отношение отрезка НЕ к отрезку НЕ характеризует величину коэффициента активности 71 и позволяет оценить степень отклонения раствора от идеальности на различных участках концентраций. Так, при больших концентрациях НКК, когда растворитель следует закону Рауля, его коэффициент активности становится равным единице. На участке же малых концентраций НКК, где выдерживается закон Генри, фугитивность равна К х, а коэффициент активности оказывается постоянным и равным [c.43]

Для аналитического определения парциальных давлений обоих компонентов системы используются законы Рауля и Генри, причем в каждом случае первый из этих законов используется для определения парциальной упругости паров растворителя, за который условно принимается преобладающий в растворе компонент, а второй закон—для определения парциальной упругости паров растворенного вещества, за которое, также условно, принимается компонент, представленный в системе в незначительной степени. [c.156]

На рис. VI, 4 изображена диаграмма р—х для одного из этих растворов (бензол—ацетон). При малых концентрациях бензола (х Смотреть страницы где упоминается термин Генри Рауля закон: [c.424] [c.323] [c.19] [c.21] [c.35] [c.193] [c.222] Физическая химия (1980) — [ c.95 ]

chem21.info

Законы Генри, Дальтона, Сеченова. Применение этих законов при лечении кессонной болезни, лечении в барокамере и исследовании электролитного состава крови

Количество газа, растворенного при данной температуре в определенном объеме жидкости, при равновесии прямо пропорциональны давлению газа.

С(Х) – концентрация газа в насыщенном растворе, моль \ л

Кг(Х) – константа Генри, зависит от природы, растворителя и температуры, моль \ л

Р(Х) – давление, Па

Закон генри лежит в основе кессонной болезни (у водолазов). При погружении происходит увеличение давления, а следовательно и растворимости газа в крови. При быстром подъеме с больших глубин происходит мгновенное выделение пузырьков газа за счет резкого уменьшения растворимости из-за падения давления. Пузырьки закупоривают кровеносные сосуды, что приводит к тяжелому поражению тканей и даже гибели.

Растворимость каждого из компонентов газовой смеси при постоянной температуре пропорциональна парциальному давлению компонента над жидкостью и не зависит от общего давления смеси.

Pi – парциальное давление компонента Xi

Pобщ – общее давление газовой смеси

χ(Xi) – молярная доля i-того компонента

при лечении газовой гангрены и ряда других заболеваний, при которых накапливаются микробы в омертвевших тканях, больных помещают в барокамеры с повышенным давлением кислорода в воздухе. При этом улучшается снабжение тканей кислородом, сто дает хорошие результаты.

Растворимость газов в жидкостях в присутствии электролитов понижается, происходит высаливание газов

С(Х) – растворимость газа Х в присутствии электролита

С₀(Х) – растворимость газа Х в чистом растворителе

С_э – концентрация электролита

Кс – константа Сеченова (зависит от природы газа, электролита, температуры)

В соответствии с законом Сеченова не только электролиты, но и белки, липиды и другие вещества, содержание которых в крови может меняться в известных пределах, оказывают существенное влияние на растворимость кислорода и углекислого газа в крови.

Коллигативные свойства разбавленных растворов. Давление пара над раствором, причины его уменьшения. Расчет давления пара над раствором (закон Рауля). Относительное понижение давления пара над раствором.

Некоторые свойства раствора зависят от теплового движения частиц, то есть определяются не природой компонентов, а количеством растворенных частиц. К ним относятся: понижение упругости пара растворителя над раствором, осмотическое давление, повышение температуры кипения, понижение температуры замерзания раствора.

1) давление пара над раствором.

Пар, находящийся в равновесии с жидкостью называют насыщенным. Давление такого пара называют давлением или упругостью насыщенного пара чистого растворителя. При данной температуре давление насыщенного чистого растворителя остается постоянным – ТД характеристика растворителя. При повышенной температуре давление насыщенного пара над растворителем повышается по принципу Ле-Шателье. Если в летучий растворитель (вода, спирт) внести нелетучее растворенное вещество (сахароза), то концентрация растворителя уменьшается, следовательно, уменьшается число частиц растворителя, переходящих в газовую фазу и давление пара растворителя падает.

В 1886 году Рауль сформулировал закон:

Давление пара раствора, содержащего нелетучее растворенное вещество, прямо пропорционально молярной доле растворителя

Р – давление пара над раствором, Па

Кр – константа Рауля, Па

χ(Х1) – молярная доля растворителя Х1, которая равна:

χ(Х1) = n(X1) \ (n(X1) + n(X2))

n(X1) и n(X2) – количество растворителя и растворенного вещества

если χ(Х1) = 1 , то Кр = Р 0 (давление пара чистого растворителя) Р = Р 0 χ(Х1)

χ(Х1) = 1 — χ(Х2) Р = Р 0 χ(1 — χ(Х2))

χ(Х2) = (Р 0 – Р) \ Р 0

Р 0 – давление пара над чистым растворителем, Па

Р – давление пара растворителя над раствором нелетучего вещества, Па

Р 0 – Р – абсолютное понижение давления пара над раствором, Па

(Р 0 – Р) \ Р 0 – относительное понижение давления пара над раствором, Па

Закон Рауля справедлив только для идеальных растворов, то есть растворов, образование которых не сопровождается химическим взаимодействием и изменением объема.

25. повышение температуры кипения растворов. Формулы расчета. Эбулиометрическая константа, эбулиометрический метод определения молярной массы растворенного вещества.

Дата добавления: 2015-04-19 ; просмотров: 8870 . Нарушение авторских прав

studopedia.info

Закон генри рауля

Кривая p = f (y) называетсялинией параи выражает зависимость давления пара над раствором от состава пара.

Интересно отметить, что даже в случае образования идеальных растворов состав пара не совпадает с составом жидкого растворадля большинства идеальных растворов. Так, парциальное давление компонента А в паре над раствором по закону Рауля равно

.

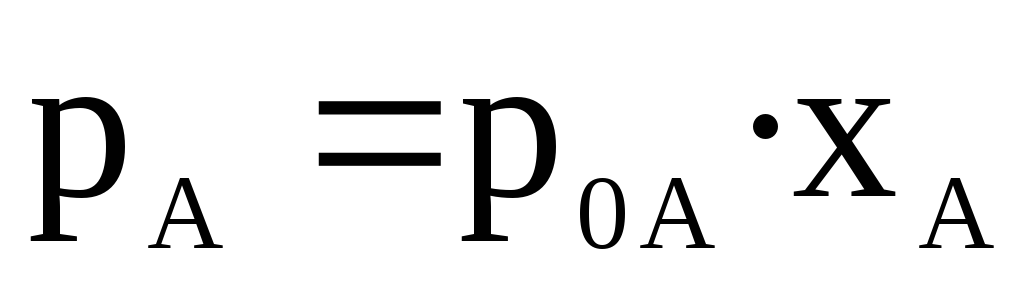x_A — мольная доля компонентаAв растворе.

С другой стороны, из закона Дальтона следует, что

, (14)

где р_общ.— общее давление пара над раствором,y_A— мольная доля компонента А в паре. Тогда

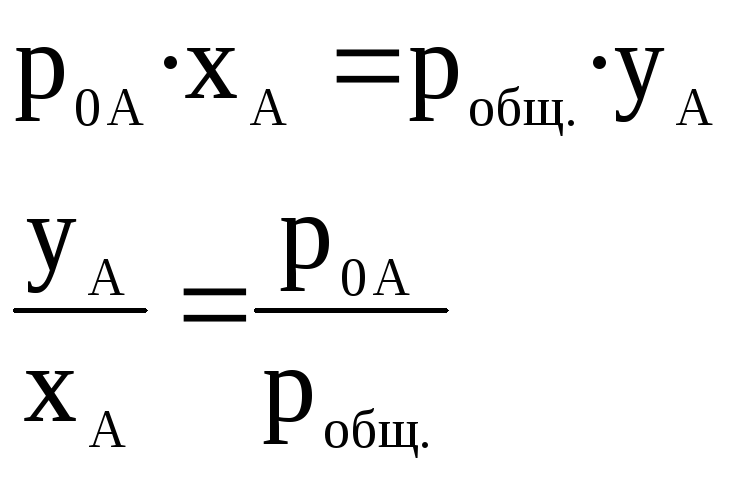
Поскольку давление пара над чистым компонентом A(р_0A) всегда больше общего давления пара для случая, представленного на рис.3, тоy_A>x_Aво всей области концентраций. Для таких систем пар обогащен компонентомAпо сравнению с жидким раствором.

С точки зрения здравого смысла (и опыта) пар должен быть обогащен более летучим компонентом (т.е. имеющим либо большее давление насыщенного пара при данной температуре Т, либо более низкую температуру кипения при заданном давлении р).

Температурой кипения раствора (Т_кип) называют температуру, при которой давление насыщенного пара над раствором равно внешнему давлению p.

Зависимость температуры кипения от состава раствора и пара представлена на рис. 4. В области I диаграммы существует только пар (раствор газов), в области II — только жидкий раствор; область III является областью сосуществования пара и жидкого раствора.

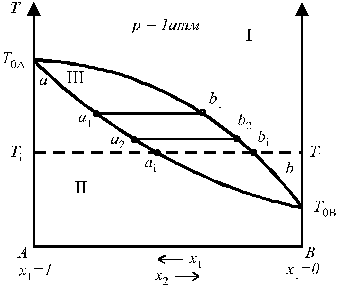
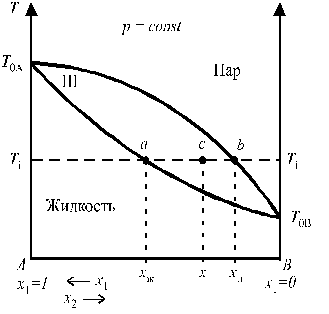
Рис. 4. Зависимость температуры

кипения от состава раствора и пара.

Рис. 5. Диаграмма состояния

бинарного раствора при применении

к ней правила рычага

T_0AиT_0B— температуры кипения чистых жидкостей А и В (более летучим компонентом является В, так какT_0A>T_0B).

Правило рычагаотношение количества (массы) двух фаз, находящихся в равновесии в гетерогенной двухфазной области, обратно пропорциональны расстояниям от соответствующих фазовых точек до фигуративной точки системы.

Для точки системы, обозначенной фигуративной точкой (с) Рис. 5, правило рычага можно записать следующим образом:

или m _жид·l _жид = m _пар·l_пар

studfiles.net

7. Растворы неэлектролитов

Состав растворов обычно выражают в весовых процентах, в молях растворенного вещества на литр раствора (молярность) или на килограмм растворителя (моляльность), а также в мольных долях.

Согласно закону Рауля, давление пара растворителя P₁ над раствором пропорционально мольной доле растворителя X₁ в растворе:

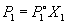
где 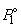– давление пара чистого растворителя при данной температуре. Для бинарного раствора закон Рауля можно представить в следующем виде:

,

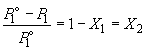то есть относительное понижение давления пара растворителя над раствором равно мольной доле X₂ растворенного вещества.

Если оба компонента раствора летучи, то закон Рауля выполняется для каждого из компонентов:

.

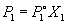
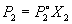Общее давление пара над раствором равно сумме парциальных давлений P₁ и P₂:

P = P₁ + P₂ = ,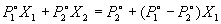

то есть давление пара линейно зависит от состава раствора.

В идеальных растворах закон Рауля выполняется для обоих компонентов во всем интервале составов.

В реальных предельно разбавленных растворах для растворителя выполняется закон Рауля, а для растворенного вещества выполняется закон Генри:

где K₂ – константа Генри. В идеальных растворах закон Генри совпадает с законом Рауля ().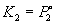

Для описания свойств реальных растворов вводится понятие активности. Активность a_i выражается в виде произведения мольной доли X_i компонента на его коэффициент активности
_i:

a_i = _iX_i.

Коэффициенты активности растворителя можно рассчитать на основании отклонений от закона Рауля:

_i = .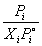

При X_i 1 _i 1, то есть a_i X_i.

Коэффициенты активности растворенного вещества можно рассчитать на основании отклонений от закона Генри:

_i = .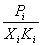

При X_i 0 _i 1, то есть a_i X_i.

Вклад компонента в любое экстенсивное свойство Z раствора определяется его парциальной мольной величиной. Парциальная мольная величина i-го компонента отражает изменение свойства Z при изменении количества i-го компонента на dn_i при постоянных P, T и составе в расчете на 1 моль:

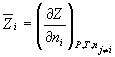
Общее значение свойства Z выражается суммой вкладов всех компонентов:

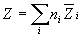
Парциальная мольная энергия Гиббса называется химическим потенциалом :

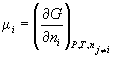
Парциальные мольные величины компонентов при постоянных P и T связаны уравнением Гиббса-Дюгема:

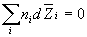
ПРИМЕРЫ

Пример 7-1. Рассчитать состав раствора бензол – толуол, который при нормальном давлении кипит при температуре 100 o C, а также состав образующегося пара. Раствор считать идеальным. Давления пара чистых бензола и толуола при 100 o C равны 1350 Торр и 556 Торр соответственно.

Решение. Мольную долю бензола в растворе находим по закону Рауля:

Мольная доля толуола в растворе равна X₂ = 1 – X₁ = 0.743.

Мольная доля бензола в паре равна

Y₁ = 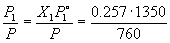= 0.456

Соответственно, мольная доля толуола в паре равна Y ₂ = 1 – Y₁ = 0.544.

Пример 7-2. Мольные объемы CCl₄ и C₆H₆ равны 0.09719 и 0.08927 л . моль –1 соответственно, а их парциальные мольные объемы в эквимолярном растворе равны 0.10010 и 0.10640 л . моль –1 . Рассчитать мольный объем эквимолярного раствора и изменение объема при смешении.

Решение. Объем раствора равен

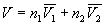= 0.5 . 0.10010 + 0.5 . 0.10640 = 0.10325 (л . моль –1 ).

Общий объем до смешения V₀ = 0.5 . 0.09719 + 0.5 . 0.08927 = 0.09323 (л . моль –1 ).

V_смеш. = V – V₀ = 0.10325 – 0.09323 = 0.01002 (л . моль –1 ).

ЗАДАЧИ

1. Давления пара чистых CHCl₃ и CCl₄ при 25 o C равны 26.54 и 15.27 кПа. Полагая, что они образуют идеальный раствор, рассчитать давление пара и состав (в мольных долях) пара над раствором, состоящим из 1 моль CHCl₃ и 1 моль CCl₄.
2. Дибромэтилен и дибромпропилен при смешении образуют почти идеальные растворы. При 80 o C давление пара дибромэтилена равно 22.9 кПа, а дибромпропилена 16.9 кПа. Рассчитать состав пара, находящегося в равновесии с раствором, мольная доля дибромэтилена в котором равна 0.75. Рассчитать состав раствора, находящегося в равновесии с паром, мольная доля дибромэтилена в котором равна 0.50.
3. Этанол и метанол при смешении образуют почти идеальные растворы. При 20 o C давление пара этанола равно 5.93 кПа, а метанола 11.83 кПа. Рассчитать давление пара раствора, состоящего из 100 г этанола и 100 г метанола, а также состав (в мольных долях) пара над этим раствором при 20 o C.
4. Давления пара чистых бензола и толуола при 60 o C равны 51.3 и 18.5 кПа. При каком давлении закипит при 60 o C раствор, состоящий из 1 моля бензола и 2 молей толуола? Каков будет состав пара?
5. Давления пара чистых C₆H₅Cl и C₆H₅Br при 140 o C равны 1.237 бар и 0.658 бар. Рассчитать состав раствора C₆H₅Cl – C₆H₅Br, который при давлении 1 бар кипит при температуре 140 o C, а также состав образующегося пара. Каково будет давление пара над раствором, полученным конденсацией образующегося пара?
6. Константа Генри для CO₂ в воде при 25 o C равна 1.25 10 6 Торр. Рассчитать растворимость (в единицах моляльности) CO₂ в воде при 25 o C, если парциальное давление CO₂ над водой равно 0.1 атм.
7. Константы Генри для кислорода и азота в воде при 25 o C равны 4.40 10 9 Па и 8.68 10 9 Па соответственно. Рассчитать состав (в %) воздуха, растворенного в воде при 25 o C, если воздух над водой состоит из 80% N₂ и 20% O₂ по объему, а его давление равно 1 бар.
8. Константы Генри для кислорода и азота в воде при 0 o C равны 2.54 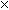10 4 бар и 5.45 10 4 бар соответственно. Рассчитать понижение температуры замерзания воды, вызванное растворением воздуха, состоящего из 80% N₂ и 20% O₂ по объему при давлении 1.0 бар. Криоскопическая константа воды равна 1.86 К . кг . моль –1 .
9. При 25 o C давление пара хлорметана над его раствором в углеводороде при разных мольных долях следующее:

www.chem.msu.su