Законы Кирхгофа. Система уравнений электрического равновесия цепи

Законы Кирхгофа. Система уравнений электрического равновесия цепи

Первый закон Кирхгофа: алгебраическая сумма мгновенных значений токов в узле равна нулю, при этом токи, втекающие в узел считают положительными, а вытекающие – отрицательными:

,

где — номер ветви, подключенной к рассматриваемому узлу.

Это уравнение называют уравнением баланса токов в узле. Первый закон Кирхгофа является следствием закона сохранения заряда, согласно которому, в любой точке электрической цепи заряды не накапливаются и не расходуются.

Второй закон Кирхгофа: алгебраическая сумма мгновенных напряжений в контуре равна нулю, при этом напряжение ветви считается положительным, если его положительное направление совпадает с направлением обхода контура, и отрицательным в противном случае.

,

где — номера ветвей, входящих в рассматриваемый контур.

Это уравнение называют уравнением баланса напряжения в контуре. Второй закон Кирхгофа является следствием закона сохранения энергии.

Уравнения составленные на основании первого и второго законов Кирхгофа, называют топологическими, т.к. они отражают свойства цепи, которые определяются только ее топологией и не зависят от того, какие элементы входят в состав ветвей.

Уравнения, устанавливающие связь между током и напряжением каждой ветви, называют компонентными (уравнениями ветвей).

На основании топологических и компонентных уравнений цепи можно составить систему уравнений, позволяющую определит токи и напряжения в цепи. Такую систему называют системой уравнений электрического равновесия цепи.

Рассмотрим последовательную RLC—цепь, изображенную на рисунке. Согласно второму закону Кирхгофа

u_L+u_C+u_R=e.

С учетом компонентных уравнений получим:

,

т.е. уравнение электрического равновесия цепи является интегро-дифференциальным уравнением. Продифференцировав последнее соотношение по времени получим:

;

т.е. уравнение электрического равновесия цепи может быть сведено к дифференциальному уравнению цепи, порядок которого равен числу независимых реактивных элементов цепи.

works.doklad.ru

Доклад законы кирхгофа

1.10. Правила Кирхгофа для разветвленных цепей

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа , которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки ( узлы ), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

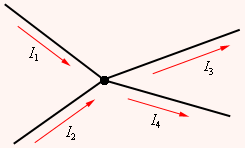
В цепи можно выделить три контура abcd , adef и abcdef . Из них только два являются независимыми (например, abcd и adef ), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd . Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура . При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.

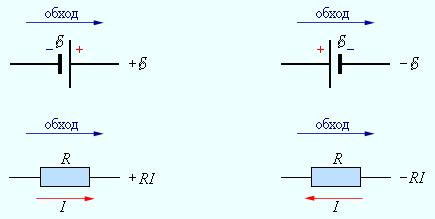
Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc : I ₁ R ₁ = Δφ _bc – 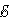₁.

Для участка da : I ₂ R ₂ = Δφ _da – 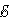₂.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφ _bc = – Δφ _da , получим:

Аналогично, для контура adef можно записать:

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура .

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I ₁, I ₂ и I ₃ имеет вид:

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

physics.ru

Территория электротехнической информации WEBSOR

Законы Кирхгофа и их применение

Воздушная линия > Постоянный ток

Законы Кирхгофа и их применение

Для расчета разветвленной сложной электрической цепи существенное значение имеет число ветвей и узлов.
Ветвью электрической цепи и ее схемы называется участок, состоящий только из последовательно включенных источников ЭДС и приемников с одним и тем же током. Узлом цепи и схемы называется место или точка соединения трех и более ветвей (узлом иногда называют и точку соединения двух ветвей).
При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

На рис. 1.13 в качестве примера показана схема электрической цепи с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с резистивными элементами без источников ЭДС (ветвь 1 — у) и с сопротивлениями, практически равными нулю (ветвь 2 — р). Так как напряжение между выводами ветви 2 — р равно нулю (сопро-тивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один.
Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна пулю:

В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, направленные к узлу, с отрицательными знаками, а направленные от узла, — с положительными.
Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В дальнейшем будет показано, что в ряде случаев целесообразно писать в одной части равенства (1.19а) алгебраическую сумму токов в ветвях, а в другой части алгебраическую сумму токов, обусловленных источниками токов:

где I — ток одной из ветвей, присоединенной к рассматриваемому узлу, a J — ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в (1.196) с положительным знаком, если направлен к узлу, и с отрицательным, если направлен от узла.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю :

при этом положительные направления для напряжений на элементах и учасчках выбираются произвольно; в уравнении (1.20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.

Часто применяется другая формулировка второго закона Кирхгофа: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящими в этот контур, равна алгебраической сумме ЭДС :

В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике довольно часто встречаются задачи анализа. Кроме того, для овладения приемами синтеза цепей необходимо предварительно изучить методы их анализа, которые преимущественно и будут в дальнейшем рассматриваться.
Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны параметры всех элементов цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа и, наконец, составить уравнения для контуров на основании второго закона Кирхгофа.
Пусть электрическая цепь содержит В ветвей и У узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно У — 1 и В — У + 1 взаимно независимых уравнений, что в сумме дает необходимое и достаточное число уравнений для определения В токов (во всех ветвях).
На основании первого закона Кирхгофа для У узлов (рис. 1.13) можно написать У уравнений:

Так как любая ветвь связывает между собой только два узла, то ток каждой ветви должен обязательно войти в эти уравнения 2 раза, причем I 12 =-I 21 ; I 13 =-I 31 и т.д.
Следовательно, сумма левых частей всех У уравнений дает тождественно нуль. Иначе говоря, одно из У уравнений может быть получено как следствие остальных У — 1 уравнений или число взаимно независимых уравнений, составленных на основании первого закона Кирхгофа, равно У — 1, т. е. на единицу меньше числа узлов. Например, в случае цепи по рис. 1.14,о с четырьмя узлами


Добавим к этим У — 1 = 3 уравнениям уравнение

Суммируя четыре уравнения, получаем тождество 0 = 0; следовательно, из этих четырех уравнений любые три независимые, например первые три (1.21а).
Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности — сечению.
Например, для поверхности S (рис. 1.14,а), как бы рассекающей электрическую схему на две части, справедливо уравнение , что можно также получить из уравнений (1.21) для узлов 3 и 4.
Чтобы установить число взаимно независимых уравнений, вытекающих из второго закона Кирхгофа, напишем для всех В ветвей схемы (рис. 1.13) В уравнений на основании закона Ома (1.11а):

где — сопротивление ветви, со-единяющей узлы р и у; Е ру — суммарная ЭДС, действующая в ветви р — у в направлении от р к у; — потенциалы узлов р и у.
В этих уравнениях суммарное число неизвестных токов В ветвей и потенциалов У узлов равняется В + У.
Не изменяя условий задачи, можно принять потенциал одного из узлов равным любому значению, в частности нулю. Если теперь из системы В уравнений (1.22) исключить оставшиеся неизвестными У — 1 потенциалов, то число уравнений уменьшится до В — (У — 1). Но исключение потенциалов из уравнений (1.22) приводит к уравнениям, связывающим ЭДС источников с напряжениями на резистивных элементах, т. е. к уравнениям, составленным на основании второго закона Кирхгофа.
Таким образом, число независимых уравнений, которые можно составить на основании второго закона Кирхгофа, равно В — (У- 1).
В качестве примера напишем уравнения, связывающие потенциалы узлов с токами и ЭДС для схемы рис. 1.14, а по ( 1.126):

Сложив третье и четвертое уравнения и вычтя полученную сумму из первого, получим

Если применим второй закон Кирхгофа (1.206) к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получим это же уравнение.
Аналогичным путем можно получить уравнения для других контуров:
для контура 1-3-2-1

для котуpa 2-4-3-2

Совместное решение любых пяти уравнений (1.21), (1.23) и (1.24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1.14, а. Если и результате решения этих уравнений получится отрицательное значение для какого-либо тока, то это значит, что действительное направление противоположно принятому за положительное.
При записи уравнений по второму закону Кирхгофа следует обращать особое внимание на то, чтобы составленные уравнения были взаимно независимыми. Контуры необходимо выбрать гак. чтобы в них вошли все ветви схемы, а в каждый из контуров — возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей. Например, контур 1-3-4-2-1 (рис. 1.14, а) можно получить из контуров 1-3-4-1 и 1-4-2-1 путем удаления ветви 1-4. Поэтому уравнение для контура 1-3-4-2-1 является следствием уравнений (1.23), (1.24а) и получается путем их суммирования. Далее будет дано наиболее общее правило выбора контуров, обеспечивающих получение независимых уравнений.
Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений (1.20) искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения U 52 (рис. 1.14, а) можно написать уравнение для контура 2-1-5-2

или для контура 5-4-2-5

откуда легко найти искомое напряжение.
Пример 1.2.
Пользуясь законами Кирхгофа, написать два выражения для тока I 0 в ветви с гальванометром (рис. 1.15), приняв известным в одном случае ток I , а в другом напряжение U .
Решение.

На основании законов Кирхгофа напишем для заданной схемы с шестью неизвестными токами уравнения:

Решив совместно эти уравнения, получим выражения для тока I 0 при заданном напряжении U

и при заданном токе I

Для полной характеристики электрического состояния цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.
В соответствии с законом сохранения энергии развиваемая всеми источниками мощность равна суммарной мощности приемников и мощности потерь в источниках (из-за внутренних сопротивлений)

В левой части (1.25) суммы алгебраические. Это значит, что если при заданных направлениях действия источника ЭДС (см. рис. 1.7) или тока (см. рис. 1.8) для тока I в источнике ЭДС или напряжения U 12 на выводах источника тока получится отрицательное численное значение, то этот источник в действительности не разовьет мощность, а получит ее от других источников. Соответствующее слагаемое в левой части (1.25) получится со знаком минус. Если требуется найти необходимую мощность источников питания цепи, то такие слагаемые следует записать с обратным знаком в правой части (1.25).

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока

www.websor.ru

Законы Кирхгофа

Академия ФСО России

Кафедра Физики

«Законы Кирхгофа и их применение для расчета электрических цепей»

Содержание

Первый закон Кирхгофа

Второй закон Кирхгофа

Расчет сложных цепей с помощью уравнений Кирхгофа

Первый закон Кирхгофа

Алгебраическая сумма токов в ветвях сходящихся к любому узлу электрической цепи тождественно равна нулю. Согласно этому закону если к некоторому узлу цепи подсоединено n ветвей с токами i ₁ i ₂ . i _n то в любой момент времени

где если направление тока положительно и ориентировано от узла (ток выходит из узла) или если ток входит в узел. Таким образом любому узлу цепи соответствует уравнение связывающее токи в ветвях цепи соединенных с данным узлом.

В качестве примера приведем схему на рисунке 1.

В соответствии с первым законом Кирхгофа:

.

Общее число уравнений которое можно составить по первому закону Кирхгофа для цепи равно числу узлов цепи .

Так для четырех узлов графа (рисунок 2) можно составить следующие четыре уравнения:

Рис.2.

узел 1:

узел 2:

узел 3:

узел 4: .

Первый закон Кирхгофа часто называют законом Кирхгофа для токов и сокращенно в тексте обозначают ЗКТ.

Число независимых уравнений равно трем так как любое из этих уравнений отличается от суммы трех остальных только знаком. Итак если цепь содержит узлов то для неё можно составить по первому закону Кирхгофа независимых уравнений. Совокупность из N узлов цепи уравнения для которых образуют систему линейно независимых уравнений называют совокупностью независимых узлов цепи .

Примеры на применение первого закона Кирхгофа. Параллельное соединение элементов

В качестве примера на применение первого закона Кирхгофа рассмотрим параллельное соединение нескольких элементов активных сопротивлений конденсаторов катушек индуктивности.

Особенностью параллельного соединения нескольких элементов является равенство напряжений приложенных к зажимам любого из элементов входящих в соединение. Цепь при таком соединении характеризуется только одним независимым узлом.

Пусть параллельно соединены n элементов активного сопротивления. Если выбрать направления отчетов токов в элементах такими как это показано на рисунке 3 то согласно первому закону Кирхгоффа при параллельном соединении элементов запишем:

;

учитывая что имеем

где .

Зависимость не отличается от зависимости между напряжением на зажимах и током в элементе активного сопротивления с проводимостью G . Следовательно цепь составленная из нескольких сопротивлении включенных параллельно может быть заменена одним активным сопротивлением при этом проводимость эквивалентного элемента равна сумме проводимостей элементов входящих в соединение.

При параллельном соединении конденсаторов (рисунок 4) ток ветви можно определить по формуле: .

Для вычисления общего тока необходимо просуммировать токи ветвей:

где _. .

Таким образом при параллельном соединении нескольких конденсаторов эквивалентная ёмкость равна сумме емкостей входящих в соединение.

В случае параллельного соединения катушек индуктивностей (рисунок 5)

Уравнение для вычисления общего тока имеет вид:

.

Следовательно то есть .

Это означает что значение эквивалентной индуктивности будит меньше наименьшего из значений соединённых параллельно индуктивностей.

Второй закон Кирхгофа

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма напряжений ветвей в любом контуре цепи тождественно равна нулю. Для замкнутого контура изображённого на рисунке 6 можно записать соотношение:

.

В соответствии со вторым законом Кирхгофа при обходе контура по часовой стрелке справедливо соотношение:

.

Изменение направления обхода эквивалентно изменению знаков напряжений на противоположные (умножению на минус единицу).

Примеры на применение второго закона Кирхгофа

Последовательное соединение элементов

В соответствии с выбранным направлением обхода по второму закону Кирхгофа получим уравнение:

характерной особенностью последовательного соединения является равенство токов в каждом из элементов входящих в соединение.

При запишем:

то есть .

Таким образом при последовательном соединении нескольких резисторов эквивалентное сопротивление равно сумме сопротивлений входящих в соединение.

При последовательном соединении катушек индуктивности (рисунок 8) можно записать:

.

Если то

следовательно .

Это означает что эквивалентная индуктивность равна сумме индуктивностей входящих в последовательное соединение.

В случае последовательного соединения конденсаторов (рисунок 9) по второму закону Кирхгофа можно записать:

Заменяя получим: .

Обратная ёмкость всех конденсаторов соединенных последовательно равна сумме обратных ёмкостей конденсаторов входящих в соединение:

.

При этом эквивалентная ёмкость соединения будет меньше наименьшей ёмкости конденсатора входящего в последовательное соединение.

Расчет сложных цепей с помощью уравнений Кирхгофа

Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера рассмотрим вариант расчета с помощью уравнений Кирхгофа электрической цепи (рисунок 10). Цепь содержит = 4 узлов и= 6 ветвей включая источники напряжения.

Для определения всех токов и напряжений в схеме достаточно найти значения токов во всех ветвях цепи. Зная ток проходящий через любую из ветвей цепи можно найти как напряжение этой ветви так и напряжение между любой парой узлов цепи.

Если мы зададимся произвольно положительными направлениями токов в ветвях цепи и пронумеруем произвольно эти токи то по первому закону Кирхгофа можно составить уравнений относительно токов в ветвях цепи.

По второму закону Кирхгофа будет линейно-независимых уравнений для напряжений ветвей схемы.

Совокупность из уравнений по первому закону Кирхгофа и уравнений составленных по второму закону Кирхгофа образует систему линейно – независимых уравнений. Эта система будет неоднородной системой уравнений так как ее свободными членами являются заданные напряжения источников.

Подобная система уравнений имеет единственное решение позволяющее найти токи в ветвях цепи а по ним и значения напряжений между любой парой узлов цепи.

Для примера составим систему уравнений по первому закону Кирхгофа (рисунок 10).

Число уравнений: .

Узел 1:

узел 2:

узел 3: .

В тоже время по второму закону Кирхгофа для контуров I II III можно составить систему из уравнений.

.

Контур I:

контур II:

контур III: .

Таким образом решая систему из 6 уравнений с шестью неизвестными токами например по методу Крамера определим неизвестные. Если в цепи будет источник тока то в системе уравнений неизвестным будет напряжение на зажимах этого источника а ток через источник будет равен току задающего источника. Общее число неизвестных сохранится прежним.

Для цепи (рисунок 11) определить токи и если E = 20 В I ₀ = 2 A R ₁ = 15 Ом R ₂ = 85 Ом.

Выберем направления токов и обхода в контуре составим уравнения по законам Кирхгофа. Число уравнений составляемых по первому закону Кирхгофа:

.

Число уравнений по второму закону Кирхгофа:

.

Уравнение токов для узла 1:

. (a)

Уравнение по второму закону Кирхгофа:

. (б)

Подставим в уравнения (а) и (б) числовые значения получим:

.

Решив эту систему определим токи и :

; .

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь 1986.

2. Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь 1998.

3. Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат. 1974.

4. В.П. Попов Основы теории цепей – М.: Высшая школа 2000

ВЕРКА ВТОРОГО ЗАКОНА КИРХГОФА Цель работы: Приобрести практические навыки работы с приборами. Научиться на практике определять падение напряжения на различных участках цепи.

Особенности и отличительные признаки параллельного и последовательного соединения резисторов, их практическая демонстрация, схематическое обоснование. Порядок сборки схемы соединения резисторов, измерение силы тока в цепи и падения напряжения на участке.

Анализ электрической цепи без учета и с учетом индуктивных связей между катушками. Определение токов методом узловых напряжений и контурных токов. Проверка по I закону Кирхгофа. Метод эквивалентного генератора. Значения токов в первой и третьей ветвях.

абораторная работа № 1 Тема : Последовательное и параллельное соединение потребителей электрической энергии. Цель работы : проверить законы параллельного и последовательного соединения

Связь комплексных амплитуд тока и напряжения в пассивных элементах электрической цепи. Законы Кирхгофа для токов и напряжений, представленных комплексными амплитудами. Применение при расчёте трёхфазных цепей.

Соотношения при последовательном соединении резисторов. Напряжение при последовательном соединении. Закон Ома для полной цепи и для ее участка. Второй закон Кирхгофа, его справедливость. Общее сопротивление при последовательном соединении резисторов.

Лабораторная работа №7 Тема: «Последовательное и параллельное соединение резисторов» Цель: Проверка на опыте особенностей последовательного и параллельного соединения резисторов.

Федеральное агентство по образованию Федеральное государственное образовательное учреждение Высшего профессионального образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

1. Исходные данные Рисунок 1 — Исходная схема 2В Таблица 1 — Данные для расчета Параметры цепи Порядок расчета цепи постоянного тока: 1. Преобразовать исходную схему до двухконтурной, заменив треугольник сопротивлений эквивалентной звездой.

Федеральное агентство по образованию Ухтинский государственный технический университет Кафедра электрификации и автоматизации технологических процессов

Определение всех неизвестных токов и сопротивления, величины и полярности с помощью законов Кирхгофа и Ома. Электрическая схема, получающаяся при замыкании ключей. Расчет схемы с двумя узлами методом узлового напряжения. Уравнение баланса мощностей.

Определение потребляемой мощности, отдаваемой всеми источниками, нахождение тока. Расчет значений реактивных сопротивлений в цепи, проверка найденных токов с помощью потенциальной диаграммы. Построение графиков изменения токов с помощью программы Mathcad.

Расчет токов и напряжения во время переходного процесса, вызванного коммутацией для каждой цепи. Классический и операторный методы. Уравнение по законам Кирхгофа в дифференциальной форме для послекоммутационного режима. Составляющие токов и напряжений.

Специфика измерения силы тока амперметром и напряжения вольтметром. Методика расчета падения напряжения на приемниках по закону Ома и по второму закону Кирхгофа на различных участках цепи. Сравнительный анализ расчетных и измерительных параметров цепи.

Методика сборки схем для наглядного изображения особенностей последовательного и параллельного соединения резисторов, описание необходимого для этого оборудования и приборов. Правила и порядок оформления результатов измерений и вычислений по схемам.

Задание на выполнение работы Схема исследуемой цепи: Рис. 1. Принципиальная схема исследуемой цепи Таблица 1. Параметры элементов схемы Элемент схемы

Цель работы: Приобретение практических навыков работы с приборами. Научиться на практике определять токи в ветвях электрической цепи. Ход работы: 1. Собрал схему согласно рисунку 1.

Министерство образования и науки Украины Донбасская государственная машиностроительная академия Кафедра электротехники и электрооборудования

ЛАБОРАТОРНАЯ РАБОТА Виды соединения резисторов. Проверка I закона Кирхгофа. Цель: проверить опытным путем справедливость соотношений при параллельном соединении резисторов, справедливость первого закона Кирхгофа.

Лабораторная работа 5 Тема : «Изучение соединений резисторов и проверка законов Ома и Кирхгофа» Цель: Проверка на опыте особенностей последовательного и параллельного соединения резисторов.

Расчет заданной схемы по законам Кирхгофа. Определение токов в ветвях методом контурных токов. Уравнение баланса мощностей, проверка его подстановкой числовых значений. Комплексные действующие значения токов в ветвях схемы. Построение векторных диаграмм.

Практические рекомендации по расчету сложных электрических цепей постоянного тока методами наложения токов и контурных токов. Особенности составления баланса мощностей для электрической схемы. Методика расчета реальных токов в ветвях электрической цепи.

Составление по данной схеме на основании законов Кирхгофа уравнений, необходимых для определения всех токов. Определение токов всех ветвей методом контурных токов. Расчет потенциалов узлов, построение графика зависимости мощности, выделяемой на резисторе.

Особенности измерения силы тока в цепи с помощью амперметра. Методика расчета силы тока в неразветвленной части электрической цепи по первому закону Кирхгофа, проверка его правильности. Анализ абсолютной и относительной погрешностей параметров цепи.

Составление на основе законов Кирхгофа системы уравнений для расчета токов в ветвях схемы. Определение токов во всех ветвях схемы методом контурных токов. Расчет системы уравнений методом определителей. Определение тока методом эквивалентного генератора.

ТипОвая расчетная работа №1. Дано: =110 В =0,2 Ом =0,4 Ом =1 Ом =60 В =50 В Найти: токи в ветвях тремя методами. Решение: Метод законов Кирхгофа. Запишем I закон Кирхгофа для узла А:

СОДЕРЖАНИЕ: 1 Перечень сокращений и условных обозначений 2 2 Задание на курсовую работу 3 3 Комплексная схема замещения 6 4 Расчет токов по законам Кирхгофа 9

аздел: Цепи постоянного тока. Тема: Законы Кирхгофа. Цепи в которых резисторы , а также источники питания соединены произвольно , называют разветвленными или сложными.

Студентам предлагаются комплексные задания, включающие теоретический расчет электрических цепей, а также сравнение рассчитанных режимов как с опытными данными (реальный эксперимент), так и с показаниями виртуальных приборов в компьютерном эксперименте

Проверка справедливости соотношений при параллельном соединении резисторов и первого закона Кирхгофа. Особенности сопротивления приемников. Методика расчета напряжения и тока для различных соединений. Сущность закона Ома для участка и для всей цепи.

Лабораторная работа. Практически убедится в физических сущности закона Ома для участка цепи. Проверить опытным путем законы Кирхгофа.

Формулировка первого и второго законов Кирхгофа, их проверка с помощью построения электрических схем в среде MicroCAP. Анализ теоремы наложения. Определение параметров эквивалентных источников энергии. Модулирование проверки законов на программном уровне.

Составление баланса мощностей для электрической схемы. Расчет сложных электрических цепей постоянного тока методом наложения токов и методом контурных токов. Особенности второго закона Кирхгофа. Определение реальных токов в ветвях электрической цепи.

ТипОвая расчетная работа №1. Дано: Е1=110 В R1=0,2 Ом R8=R9=0,4 Ом R5=R6=1 Ом U5=60 В U6=50 В Найти: токи в ветвях тремя методами. Решение: Метод законов Кирхгофа.

refy.ru