Законы отражения и преломления света принцип ферма

Все законы геометрической оптики следуют из закона сохранения энергии. Все эти законы не являются независимыми друг от друга.

4.3.1. Закон независимого распространения лучей

Если через точку пространства проходит несколько лучей, то каждый луч ведет себя так, как если бы других лучей не было.

Это справедливо для линейной оптики, где показатель преломления не зависит от амплитуды и интенсивности проходящего света.

4.3.2. Закон обратимости

Траектория и длина хода лучей не зависят от направления распространения.

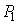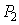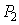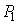То есть, если луч, который распространяется от точки до точки , пустить в обратном ходе (от к ), то он будет иметь такую же траекторию, как и в прямом.

4.3.3. Закон прямолинейного распространения

4.3.4. Закон преломления и отражения

Закон отражения и преломления подробно рассматривается в Главе 3. В рамках геометрической оптики формулировки законов преломления и отражения сохраняются.

4.3.5. Принцип таутохронизма

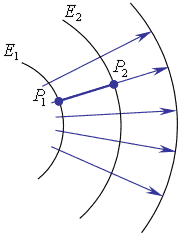
Рис.4.3.1. Принцип таутохронизма.

Рассмотрим распространение света, как распространение волновых фронтов (рис.4.3.1).

Оптическая длина любого луча между двумя волновыми фронтами одна и та же:

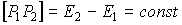
Волновые фронты – поверхности, которые оптически параллельны друг другу. Это справедливо и для распространения волновых фронтов в неоднородных средах

4.3.6. Принцип Ферма

Пусть имеются две точк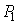и и 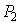, расположенные, возможно, в различных средах. Эти точки можно соединить между собой различными линиями. Среди этих линий будет только одна, которая будет являться оптическим лучом, который распространяется в соответствии с законами геометрической оптики (рис.4.3.2).

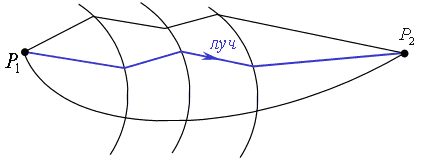
Рис.4.3.2. Принцип Ферма.

Можно сосчитать для сравнения оптическую длину этого луча и каких-либо других линий. В результате такого сравнения был получен принцип Ферма (Fermat principle).

Оптическая длина луча между двумя точками минимальна по сравнению со всеми другими линиями, соединяющими эти две точки:

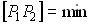
Существует более полная формулировка:

Оптическая длина луча между двумя точками является стационарной по отношению к смещению этой линии.

Луч – кратчайшее расстояние между двумя точками. Если линия, вдоль которой мы измеряем расстояние между двумя точками, отличается от луча на величину 1-го порядка малости, то оптическая длина этой линии отличается от оптической длины луча на величину 2-го порядка малости.

Если оптическую длину луча, соединяющего две точки, поделить на скорость света, то получим время, необходимое на преодоление расстояния между двумя точками:

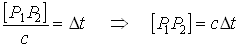(4.3.3)

Еще одна формулировка принципа Ферма:

Луч, соединяющий две точки, идет по такому пути, который требует наименьшего времени (по самому быстрому пути).

Из этого принципа могут быть выведены законы преломления, отражения и т.д.

4.3.7 Закон Малюса-Дюпена

Нормальная конгруэнция сохраняет свойства нормальной конгруэнции в процессе прохождения через различные среды.

4.3.8 Инварианты

Инварианты (от слова неизменный) – это соотношения, выражения, которые сохраняют свой вид при изменении каких-либо условий, например, при прохождении света через различные среды или системы.

Интегральный инвариант Лагранжа

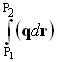
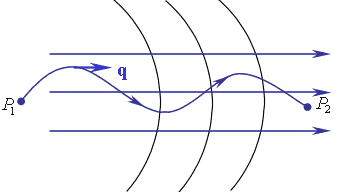
Рис.4.3.3. Интегральный инвариант Лагранжа.

Дифференциальный инвариант Лагранжа

Луч в пространстве полностью описывается радиус-вектором 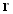, который содержит три линейные координаты 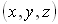, и оптическим вектором 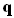, который содержит три угловые координаты 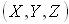. Всего, таким образом, имеется 6 параметров для определения некоторого луча в пространстве. Однако из этих 6 параметров только 4 являются независимыми, так как можно получить два уравнения, которые связывают параметры луча друг с другом.

Первое уравнение определяется из длины оптического вектора:

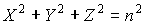(4.3.5)

где 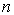– показатель преломления среды.

Второе уравнение вытекает из условия ортогональности векторов 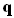и :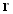

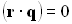
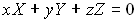(4.3.6)

Из выражений (4.3.5) и (4.3.6), воспользовавшись аналитической геометрией, можно вывести следующее соотношение:

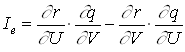
Дифференциальный инвариант Лагранжа:
Величина 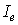сохраняет свое значение для данного луча при распространении пучка лучей через любую совокупность оптических сред.

Инвариант Штраубеля

Рассмотрим в пространстве бесконечно малые площадк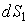и и 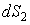, находящиеся на некотором расстоянии друг от друга (рис.4.3.4). Углы 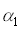и 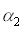– углы между нормалями к площадкам и направлением луча.

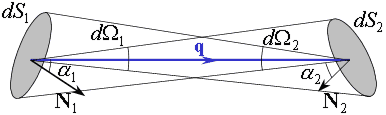
Рис.4.3.4. Световая трубка.

Если мы соединим все возможные точки краев площадки друг с другом, то получим так называемую лучевую (световую) трубку.

Геометрический фактор лучевой трубки записывается так:

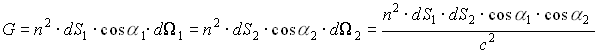(4.3.8)

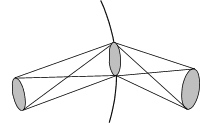
Рис.4.3.5. Инвариант Штраубеля.

Инвариант Штраубеля:
Геометрический фактор остается инвариантным при распространении лучевой трубки через любую последовательность различных сред (рис.4.3.5).

Инвариант Штраубеля выражает закон сохранения энергии, так как он показывает неизменность лучистого потока.

Из определения яркости (2.1.11) можно получить следующее равенство:

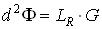(4.3.9)
где 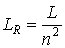– приведенная яркость, которая инвариантна, как уже было сказано в главе 2.

aco.ifmo.ru

Принцип Ферма

Принцип минимального времени

В 1660 г. П. Ферма, сформулировал принцип, который явился обобщенным законом и геометр ической оптики. В простейшей формулировке этот принцип звучит так.

В вакууме скорость света максимальна. В оптической среде с показателем преломления п время прохождения светом того же расстояния увеличивается в п раз. Величина s , равная п po изведению абсолютного показателя преломления n на пройденном расстояние l ( s = nl ), называется оптической длиной пути. Принцип Ферма относится именно к оптической длине пути

Прямолинейность распространения света.

Используя принцип Ферма, можно получить закон прямолинейного распространении света. Свет из одной точки в другую распространяется по крат чайшему расстоянию. В однородной среде кратчайшим оптически и путем является прямая линия.

Однако в неоднородной среде кратчайшим оптическим путем может оказаться некоторая кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометри ческой прямой. Этим объясняется явление преломления света и ис кривление световых лучей в неоднородной среде — явление ре фракции.

Закон отражения.

Пусть на зеркальную поверхность падает свет из точки А. В точке А’ собираются лучи, отраженные от зеркала. Предположим, что свет из точки А в точку А’ может распространяться двумя путями — отражаясь от точек О и О’. Время, которое потребуется свету, чтобы пройти из источника А в точку А’ через точку О, можно определить из вы ражения

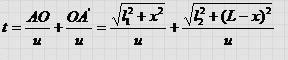
Здесь u — скорость распространения света. Покажем, что время прохождения света по траектории АОА’ меньше, чем по любой другой траектории АО’А’.

Продифференцируем выражение и приравняем произ водную нулю в соответствии с принципом Ферма.

Учтем, что sin a = x / AO , sin a ’ = ( L — х) /ОА’. Получим:

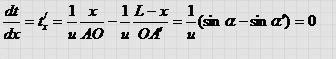
Отсюда получаем sin a = sin a ‘; а так как оба угла острые, то отсюда следует равенство углов:

Мы получили соотношение, выражающее закон отражения угол отражения a ‘ равен углу падения a . Из принципа Ферма следует и вторая часть этого закона: отраженный луч лежит в плоскости, проходящей через падающий луч и нормаль сражающей поверхности. Ведь если бы эти лучи лежали в разных плоскостях, то не был бы минимальным путь АОА’.

Закон преломления света

Закон преломления света. Аналогичным образом, используя принцип Ферма, рассмотрим явление, происходящее на границе разд ела двух сред. Пусть в среде I скорость света u ₁ , в среде II — u ₂ . Для прохождения света из точки А₁ в точку A ₂ будет затрачено время

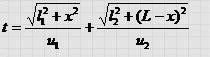
Выберем из всех возможных траекторий распространения света ту, которой соответствует минимальное время распростране ния света. Продифференцировав и положив производную равной пулю, получим:

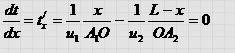
Учитывая, что sin a 1 = x / A 1 O , sin a 2 = ( L — х) /ОА2 получим : 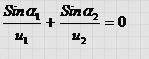Откуда следует :

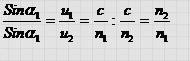
Это и есть закон преломления света. Запишем его в более удобной форме.

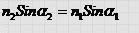
Из построений и принципа Ферма следует также, что преломленный луч лежит в плоскости, проходящей через падающий луч и перпендикуляр к поверхности раздела двух сред.

Рассматривая падение светового пучка на границу раздела двух сред, мы говорили раздельно об отражении и преломлении света. Это было вызвано необходимостью вывода законов отражения и преломления света. Однако практически всегда на границе раздела двух сред световой пучок разделяется на два — отраженный и преломленный.

optika-zaharova.narod.ru

Основные законы геометрической оптики известны ещё с древних времен. Так, Платон (430 г. до н.э.) установил закон прямолинейного распространения света. В трактатах Евклида формулируется закон прямолинейного распространения света и закон равенства углов падения и отражения. Аристотель и Птолемей изучали преломление света. Но точных формулировок этих законов геометрической оптики греческим философам найти не удалось.

Геометрическая оптика является предельным случаем волновой оптики, когда длина световой волны стремится к нулю.

Простейшие оптические явления, например возникновение теней и получение изображений в оптических приборах, могут быть поняты в рамках геометрической оптики.

В основу формального построения геометрической оптики положено четыре закона, установленных опытным путем:

· закон прямолинейного распространения света;

· закон независимости световых лучей;

· закон преломления света.

Для анализа этих законов Х. Гюйгенс предложил простой и наглядный метод, названный впоследствии принципом Гюйгенса.

Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

Основываясь на своем методе, Гюйгенс объяснил прямолинейность распространения света и вывел законы отражения и преломления.

Закон прямолинейного распространения света:

· свет в оптически однородной среде распространяется прямолинейно.

Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их источниками малых размеров.

Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит через очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия.

Тень, отбрасываемая предметом, обусловлена прямолинейностью распространения световых лучей в оптически однородных средах.

Астрономической иллюстрацией прямолинейного распространения света и, в частности, образования тени и полутени может служить затенение одних планет другими, например затмение Луны, когда Луна попадает в тень Земли (рис. 7.1). Вследствие взаимного движения Луны и Земли тень Земли перемещается по поверхности Луны, и лунное затмение проходит через несколько частных фаз (рис. 7.2).

Закон независимости световых пучков:

· эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.

Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо.

· отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;

· угол падения α равен углу отражения γ: α = γ

Для вывода закона отражения воспользуемся принципом Гюйгенса. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред (рис. 7.4). Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.

· Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.

Закон преломления (закон Снелиуса) (рис. 7.5):

· луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;

· отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.

Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна u (рис. 7.6).

Пусть время, затрачиваемое волной для прохождения пути ВС, равно Dt. Тогда ВС = сDt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = uDt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. 7.6 видно, что

, т.е. .

Отсюда следует закон Снелиуса:

.

Несколько иная формулировка закона распространения света была дана французским математиком и физиком П. Ферма.

Физические исследования относятся большей частью к оптике, где он установил в 1662 г. основной принцип геометрической оптики (принцип Ферма). Аналогия между принципом Ферма и вариационными принципами механики сыграла значительную роль в развитии современной динамики и теории оптических инструментов.

Согласно принципу Ферма, свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.

Покажем применение этого принципа к решению той же задачи о преломлении света.

Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела (рис. 7.7).

В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

.

Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

,

отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: .

Принцип Ферма сохранил свое значение до наших дней и послужил основой для общей формулировки законов механики (в том числе теории относительности и квантовой механики).

Из принципа Ферма вытекает несколько следствий.

Обратимость световых лучей: если обратить луч III (рис. 7.7), заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.

Другой пример – мираж, который часто наблюдают путешественники на раскаленных солнцем дорогах. Они видят впереди оазис, но когда приходят туда, кругом оказывается песок. Сущность в том, что мы видим в этом случае свет, прошедший над песком. Воздух сильно раскален над самой дорогой, а в верхних слоях холоднее. Горячий воздух, расширяясь, становится более разреженным и скорость света в нем больше, чем в холодном. Поэтому свет проходит не по прямой, а по траектории с наименьшим временем, заворачивая в теплые слои воздуха.

Если свет распространяется из среды с большим показателем преломления (оптически более плотной) в среду с меньшим показателем преломления (оптически менее плотной) ( > ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α (рис. 7.8 а).

С увеличением угла падения увеличивается угол преломления (рис. 7.8 б, в), до тех пор, пока при некотором угле падения ( ) угол преломления не окажется равным π/2.

Угол называется предельным углом. При углах падения α > весь падающий свет полностью отражается (рис. 7.8 г).

· По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.

· Если , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 7.8 г).

· Таким образом, при углах падения в пределах от до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Предельный угол определим из формулы:

;

.

Явление полного отражения используется в призмах полного отражения (Рис. 7.9).

Показатель преломления стекла равен n » 1,5, поэтому предельный угол для границы стекло – воздух = arcsin (1/1,5) = 42°.

При падении света на границу стекло – воздух при α > 42° всегда будет иметь место полное отражение.

На рис. 7.9 показаны призмы полного отражения, позволяющие:

а) повернуть луч на 90°;

б) повернуть изображение;

в) обернуть лучи.

Призмы полного отражения применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя , определяем относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).

Явление полного отражения используется также в световодах, представляющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала.

В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцевина) которого окружается стеклом – оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углам больше предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение и распространяется только по световедущей жиле.

Световоды используются при создании телеграфно-телефонных кабелей большой емкости. Кабель состоит из сотен и тысяч оптических волокон тонких, как человеческий волос. По такому кабелю, толщиной в обычный карандаш, можно одновременно передавать до восьмидесяти тысяч телефонных разговоров.

Кроме того, световоды используются в оптоволоконных электронно-лучевых трубках, в электронно-счетных машинах, для кодирования информации, в медицине (например, диагностика желудка), для целей интегральной оптики.

ens.tpu.ru