Правила линейной функции и её графика

Линейная функция и ее график

Алгоритм построения графика уравнения ах + by + с = 0, который мы сформулировали в § 28, при всей его четкости и определенности математикам не очень нравится. Обычно они выдвигают претензии к первым двум шагам алгоритма. Зачем, говорят они, дважды решать уравнение относительно переменной у: сначала ах1 + Ьу + с = О, затем ахг + Ьу + с = О? Не лучше ли сразу выразить у из уравнения ах + by + с = 0, тогда легче будет проводить вычисления (и, главное, быстрее)? Давайте проверим. Рассмотрим сначала уравнение 3x — 2у + 6 = 0 (см. пример 2 из § 28).

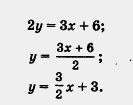
Придавая х конкретные значения, легко вычислить соответствующие значения у. Например, при х = 0 получаем у = 3; при х = -2 имеем у = 0; при х = 2 имеем у = 6; при х = 4 получаем: у = 9.

Видите, как легко и быстро найдены точки (0; 3), (- 2; 0), (2; 6) и (4; 9), которые были выделены в примере 2 из § 28.

Точно так же уравнение Ьх — 2у = 0 (см. пример 4 из § 28) можно было преобразовать к виду 2у =16 -3x . далее у = 2,5x; нетрудно найти точки (0; 0) и (2; 5), удовлетворяющие этому уравнению.

Наконец, уравнение 3x + 2у — 16 = 0 из того же примера можно преобразовать к виду 2y = 16 -3x и далее 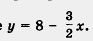нетрудно найти точки (0; 0) и (2; 5), которые ему удовлетворяют.

Рассмотрим теперь указанные преобразования в общем виде.

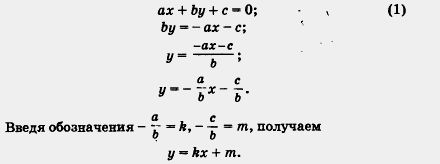
Таким образом, линейное уравнение (1) с двумя переменными х и у всегда можно преобразовать к виду
y = kx + m,(2) где k,m — числа (коэффициенты), причем .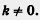

Этот частный вид линейного уравнения будем называть линейной функцией.

С помощью равенства (2) легко, указав конкретное значение х, вычислить соответствующее значение у. Пусть, например,

у = 2х + 3. Тогда:
если х = 0, то у = 3;
если х = 1, то у = 5;
если х = -1, то у = 1;
если х = 3, то у = 9 и т. д.

Обычно эти результаты оформляют в виде таблицы:

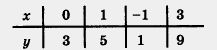
Значения у из второй строки таблицы называют значениями линейной функции у = 2х + 3, соответственно, в точках х = 0, х = 1, х = -1,х=-3.

В уравнении (1) переменные хну равноправны, а в уравнении (2) — нет: конкретные значения мы придаем одной из них — переменной х, тогда как значение переменной у зависит от выбранного значения переменной х. Поэтому обычно говорят, что х — независимая переменная (или аргумент), у — зависимая переменная.

Обратите внимание: линейная функция — это специальный вид линейного уравнения с двумя переменными. Графиком уравнения у — kx + т, как всякого линейного уравнения с двумя переменными, является прямая — ее называют также графком линейной функции y = kx + тп. Таким образом, справедлива следующая теорема.

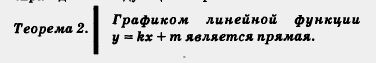
Пример 1. Построить график линейной функции у = 2х + 3.

Решение. Составим таблицу:

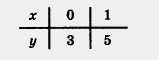
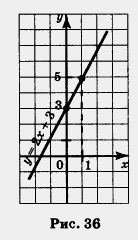
Построим на координатной плоскости хОу точки (0; 3) и (1; 5) и проведем через них прямую. Это и есть график линейной функции у = 2х + 3 (рис. 36).

Замечание. В § 25 мы уже говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введенное понятие требует уточнения, развития. Именно так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы еще довольно долго будем привыкать к нему, набираться опыта, работать с этим понятием пока не придем к строгому определению (зто будет в 9 классе).

Практические задания

Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.Приведем примеры.

Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?

Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у — 500 + ЗОд:. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации.

Теперь нетрудно установить, что:

при х = 2 имеем у = 560 (в уравнение у = ЗОд: + 500 подставили
х = 2 и получили у = 560);
при х = 4 имеем у = 620;
при х = 10 имеем у = 800.

Вторая ситуация. На складе было 500 т угля. Ежедневно стали увозить по 30 т угля. Сколько угля будет на складе через 2, 4,10 дней?

Здесь математической моделью ситуации является линейная функция у = 500 — З0x. С помощью этой модели нетрудно ответить на вопрос задачи:

если х = 2, то у = 440 (в уравнение у = 500 — З0x подставили
х — 2 и получили у = 440);
если х = 4, то у = 380;
если х = 10, то у = 200.

Третья ситуация. Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?

Математической моделью ситуации является линейная функция у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А (в километрах). С помощью этой модели отвечаем на вопрос задачи:

если х = 2, то у = 23 (в уравнение у = 15 + 4д: подставили х = 2
и получили у = 23);
если д: = 4, то у = 31;
если х = 6, то у = 39.

На самом деле во всех математических моделях этих трех ситуаций мы допустили неточности, поскольку ничего не сказали о тех ограничениях на х, которые вытекают из смысла задачи. Ведь ясно, что в первой ситуации независимая переменная х может принимать только значения 1, 2, 3, . поскольку х — число дней.

Следовательно, уточненная математическая модель первой ситуации выглядит так:

Во второй ситуации независимая переменная х, обозначающая, как и в первой ситуации, число дней, может принимать только значения 1, 2, 3, . 16. Действительно, если х = 16, то по формуле у = 500 — З0x находим: у = 500 — 30 • 16 = 20. Значит, уже на 17-й день вывезти со склада 30 т угля не удастся, поскольку на складе к этому дню останется всего 20 т и процесс вывоза угля придется прекратить. Следовательно, уточненная математическая модель второй ситуации выглядит так:

у = 500 — ЗОд:, где х = 1, 2, 3, . 16.

В третьей ситуации независимая переменная х теоретически может принять любое неотрицательное значение (напр., значение х = 0, значение х = 2, значение х = 3,5 и т. д.), но практически турист не может шагать с постоянной скоростью без сна и отдыха сколько угодно времени. Значит, нам нужно было сделать разумные ограничения на х, скажем, 0 0?
в) при каких значениях х будет у 0 при х > 3. В самом деле если х > 3, то прямая расположена выше оси ж, значит, ординаты соответствующих точек прямой положительны.

в) у 0 (получили х > 3);
в) неравенство 2x — 6 0, то линейная функция у = kx + m возрастает.

Рассмотрим график линейной функции, изображенный на рисунке 49, б. Если двигаться по этому графику слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин убывание и говорят так: если k

edufuture.biz

Линейная функция « y = kx + b » и её график

Прежде чем перейти к изучению функции « y = kx » внимательно изучите урок
«Что такое функция в математике» и «Как решать задачи на функцию».

Функцию вида « y = kx + b » называют линейной функцией.

Буквенные множители « k » и « b » называют числовыми коэффициентами .

Вместо « k » и « b » могут стоять любые числа (положительные, отрицательные или дроби).

Другими словами, можно сказать, что « y = kx + b » — это семейство всевозможных функций, где вместо « k » и « b » стоят числа.

Примеры функций типа « y = kx + b ».

Давайте определим для каждой функций выше, чему равны числовые коэффициенты « k » и « b » .

Обратите особое внимание на функцию « y = 0,5x » в таблице. Часто совершают ошибку при поиске в ней числового коэффициента « b ».

Рассматривая функцию « y = 0,5x », неверно утверждать, что числового коэффициента « b » в функции нет.

Числовый коэффициент « b » присутствет в функции типа « y = kx + b » всегда. В функции « y = 0,5x » числовый коэффициент « b » равен нулю .

Как построить график линейной функции
« y = kx + b »

Графиком линейной функции « y = kx + b » является прямая .

Так как графиком функции « y = kx + b » является прямая линия , функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств), что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что чтобы построить график функции вида
« у = kx + b » нам достаточно будет найти всего две точки.

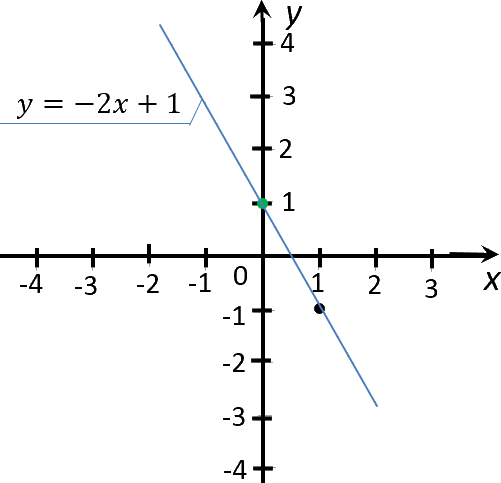
Для примера построим график функции « y = −2x + 1 ».

Найдем значение функции « y » для двух произвольных значений « x ». Подставим, например, вместо « x » числа « 0 » и « 1 ».

Выбирая произвольные числовые значения вместо « x », лучше брать числа « 0 » и « 1 ». С этими числами легко выполнять расчеты.

Полученные значения « x » и « y » — это координаты точек графика функции.

Запишем полученные координаты точек « y = −2x + 1 » в таблицу.

Отметим полученные точки на системе координат.

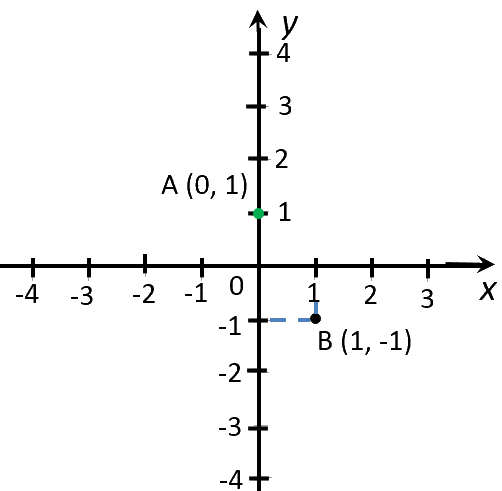
Теперь проведем прямую через отмеченные точки. Эта прямая будет являться графиком функции « y = −2x + 1 ».

Как решать задачи на
линейную функцию « y = kx + b »

Построить график функции « y = 2x + 3 ». Найти по графику:

• значение « y » соответствующее значению « x » равному −1; 2; 3; 5 ;
• значение « x », если значение « y » равно 1; 4; 0; −1 .

Вначале построим график функции « y = 2x + 3 ».

Используем правила, по которым мы строили график функции выше. Для построения графика функции « y = 2x + 3 » достаточно найти всего две точки.

Выберем два произвольных числовых значения для « x ». Для удобства расчетов выберем числа « 0 » и « 1 ».

Выполним расчеты и запишем их результаты в таблицу.

Отметим полученные точки на прямоугольной системе координат.



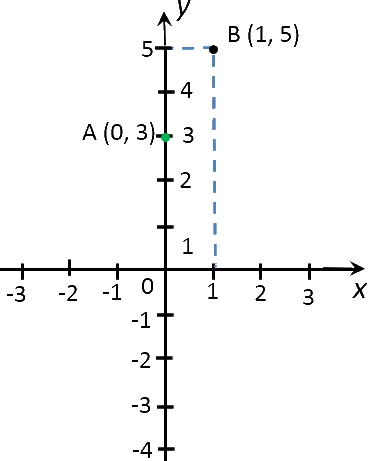
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции « y = 2x + 3 ».



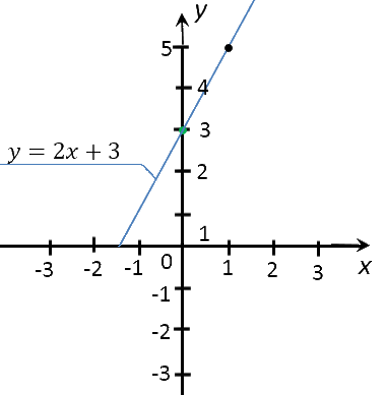
Теперь работаем с построенным графиком функции « y = 2x + 3 ».

Требуется найти значение « y », соответствующее значению « x »,
которое равно −1; 2; 3; 5 .

Тему «Как получить координаты точки функции» с графика функции мы уже подробно рассматривали в уроке «Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

Чтобы найти значение « y » по известному значению « x » на графике функции необходимо:

1. провести перпендикуляр от оси « Ox » (ось абсцисс) из заданного числового значения « x » до пересечения с графиком функции;
2. из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси « Oy » (ось ординат);
3. полученное числовое значение на оси « Oy » и будет искомым значением.

   По правилам выше найдем на построенном ранее графике функции « y = 2x + 3 » необходимые значения функции « y » для « x » равным −1; 2; 3; 5 .

   math-prosto.ru

   Построение графика линейной функции

   Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

   График линейной функции – прямая линия. Прямую можно провести через две точки.

   Чтобы построить график линейной функции вида , нужно:

4. вычислить координаты любых двух точек (взять любые два значения аргумента и вычислить соответствующие два значения
5. для каждой пары найти точку в системе координат, и провести прямую через эти две точки.

   Пример для функции :

   

   Проще всего найти функцию, если аргумент: .

   Итак, первая точка имеет координаты .

   Теперь возьмем любое другое число в качестве , например, .

   Вторая точка имеет координаты .

   Угловой коэффициент – это тангенс угла наклона прямой. Для его нахождения выберем две точки и на графике и построим прямоугольный треугольник с гипотенузой

   

   Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция, и с чем ее едят. Если ты считаешь себя профи по части линейных функций, добро пожаловать. Но если нет, тебе стоит прочитать тему «Линейная функция».

   Начнем с небольшой проверки:

   Как выглядит линейная функция в общем виде (формула)?

   Почему она называется линейной?

   Как влияет коэффициент при на график линейной функции?

   Если ты сходу смог ответить на эти вопросы, продолжай читать. Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».

   Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить график по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?

   Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.

   Итак, дамы и господа, линейная функция: .

   Построение графика линейной функции: ты берешь два каких-либо икса, (например, и ), подставляешь их в формулу, находишь соответствующие игреки.

   Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.

   Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.

   Разберем пример:

   Постройте график уравнения .

   Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам. Это да, но можно сделать проще и интересней.

   Выясним, в какой точке эта прямая будет пересекать ось . Что характерно для этой точке? Правильно, . Так и пишем:

   А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось ?

   Вот и они – две точки графика. Осталось только приложить линейку:

   

   Согласись, это было быстро и просто?

   А теперь сам:

   Ладно, а как еще можно задать функцию?

   Ну, например словесно:

   Прямая проходит через точку , а ее угловой коэффициент равен .

   Ну что же, вспоминаем: что такое угловой коэффициент?

   Это, с одной стороны, коэффициент при , а с другой – это тангенс угла между прямой и осью . Вот это мы и используем когда делаем построение графика линейной функции: ставим точку , и рисуем прямоугольный треугольник так, что один его катет параллелен оси , а другой – перпендикулярен. При этом второй катет должен быть ровно в раз больше первого. Очень удобно в этом случае, чтобы первый катет был равен , тогда второй будет равен :

   

   Теперь реши сам:

   Прямая, уравнение которой имеет вид ( неизвестно), проходит через точку . Постройте ее.

   Должно получиться вот так:

   

   Еще пример:

   Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку и параллельной прямой . Строить график прямой нельзя.

   О, это что-то новенькое. Про параллельность прямых мы еще не учили.

   Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:

   

   Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты и . И сразу становится ясно: раз отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось – секущая), значит, у них одинаковый коэффициент !

   Вернемся к задаче. Напомню условие:

   Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку и параллельной прямой .

   Итак, угловой коэффициент нашей прямой равен угловому коэффициенту прямой , то есть . Теперь задача становится точь в точь как мы решали до этого:

   

   График пересекает ось ординат в точке . Это и есть коэффициент :

   И снова пример для самостоятельного решения:
   Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку и параллельной прямой . Строить график прямой нельзя.

   Ответ: .

   И еще один тип прямых. Самый простой из всех:

   Хм… Даже на линейную функцию непохоже, чего это он самый простой?

   А вот почему: достаточно небольшого преобразования, и получится самая обычная линейная функция:

   А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…

   Ладно, ничего сложного здесь нет: . Это и есть все отличие от обычной прямой : просто надо будет выколоть из графика одну точку: .

   

   Ответ:

   Ну вот, ты увидел, как можно строить график любой линейной функции. Конечно, можно было бы придумать еще миллион «интересных случаев», но хватит терять время на эту халявную тему, пора уже перейти к более серьезным вещам.

   Комментарии

   Распространение материалов без согласования допустимо при наличии dofollow-ссылки на страницу-источник.

   Политика конфиденциальности

   Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

   Сбор и использование персональной информации

   Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

   От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

   Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

   Какую персональную информацию мы собираем:

6. Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Спасибо за сообщение!

Ваш комментарий принят, после модерации он будет опубликован на данной странице.

Хотите узнать что скрыто под катом и получать эксклюзивные материалы по подготовке к ОГЭ и ЕГЭ? Оставьте e-mail

youclever.org

Линейная функция и ее график (В.А.Тарасов)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти



На данном уроке мы познакомимся с понятием линейной функции, выведем ее в общем виде и рассмотрим частные случаи. Введем новую терминологию, рассмотрим типовые задачи и элементарные примеры.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Числовые функции» и «Функции»

Напоминание некоторых теоретических фактов и решение опорной задачи

В предыдущих уроках мы изучали линейное уравнение с двумя переменными, это уравнение вида , . Мы выяснили, что графиком данного уравнения является прямая. Рассмотрим пример:

(1)

Перепишем его таким образом, чтобы у был в одной части, а все остальное в другой:





Перенесем у в левую часть, а все остальное в правую:

(2)

Мы получили частный случай уравнения 1, в котором стоит обособленно в левой части, графиком обоих выражений будет одна и та же прямая, но запись 2 мы будем называть линейной функцией у от х.

Построим график данной функции, для этого составим таблицу:



Рис. 1. График функции y=2x-3

Выведение линейной функции и ее параметров в общем случае, введение новых терминов

Определим линейную функцию в общем случае из линейного уравнения с двумя переменными:





Поскольку можем обе части поделить на b:



Введем более удобные обозначения:

,

(3)

Для примера №1 ,

Таким образом, пара чисел k и m задают конкретную линейную функцию.

Введем некоторую терминологию. В линейной функции переменную х называют независимой переменной или аргументом функции, мы сами можем выбирать произвольное значение х и по нему находить соответствующее значение у.

называют зависимой переменной или функцией.

Линейная функция характеризуется тем, что если задано значение х, можно сразу получить значение у. у – это линейная функция от х.

Найдем для линейной функции в общем виде (3) точки пересечения с осями. Для всех точек на оси у характерно то, что их абсцисса – координата х, равна нулю.

, ;

Точка пересечения с осью у: (0, m)

Отсюда геометрический смысл переменной m – это ордината точки пересечения прямой 3 с осью у. Параметр m однозначно задает точку пересечения прямой 3 с осью ординат.

Параметр носит название угловой коэффициент.

Для всех точек на оси х характерно то, что их ордината равна нулю. Найдем точку пересечения нашей функции с осью х:

, , ,

Точка пересечения с осью х: ()

Решение примера, выявление свойств параметров линейной функции

Построим графики двух линейных функций: (4), (5)

В функции 4

В функции 5

Для построения графиков составим таблицы, в которых запишем точки их пересечения с осями координат:

interneturok.ru