Как записать закон движения точки x t

1.3. Равномерное движение

Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью . Такое движение называется равномерным . При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x . Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX . Поэтому перемещение и скорость при прямолинейном движении можно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.

Если в некоторый момент времени t ₁ тело находилось в точке с координатой x ₁ , а в более поздний момент t ₂ – в точке с координатой x ₂ , то проекция перемещения Δ s на ось OX за время Δ t = t ₂ – t ₁ равна

Эта величина может быть и положительной и отрицательной в зависимости от направления, в котором двигалось тело. При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем. Скоростью равномерного прямолинейного движения называют отношение

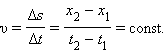
Если υ > 0 , то тело движется в сторону положительного направления оси OX ; при υ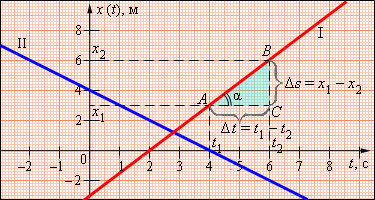

Для закона движения, изображенного на графике I (рис. 1.3.1), при t = 0 тело находилось в точке с координатой x ₀ = –3 . Между моментами времени t ₁ = 4 с и t ₂ = 6 с тело переместилось от точки x ₁ = 3 м до точки x ₂ = 6 м . Таким образом, за Δ t = t ₂ – t ₁ = 2 с тело переместилось на Δ s = x ₂ – x ₁ = 3 м . Следовательно, скорость тела составляет

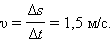
Величина скорости оказалась положительной. Это означает, что тело двигалось в положительном направлении оси OX . Обратим внимание, что на графике движения скорость тела может быть геометрически определена как отношение сторон BC и AC треугольника ABC (см. рис. 1.3.1)

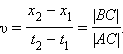
Чем больше угол α , который образует прямая с осью времени, т. е. чем больше наклон графика ( крутизна ), тем больше скорость тела. Иногда говорят, что скорость тела равна тангенсу угла α наклона прямой x ( t ) . С точки зрения математики это утверждение не вполне корректно, так как стороны BC и AC треугольника ABC имеют разные размерности : сторона BC измеряется в метрах, а сторона AC – в секундах.

Аналогичным образом для движения, изображенного на рис. 1.3.1 прямой II, найдем x ₀ = 4 м , υ = –1 м/с .

На рис. 1.3.2 закон движения x ( t ) тела изображен с помощью отрезков прямых линий. В математике такие графики называются кусочно-линейными . Такое движение тела вдоль прямой не является равномерным . На разных участках этого графика тело движется с различными скоростями, которые также можно определить по наклону соответствующего отрезка к оси времени. В точках излома графика тело мгновенно изменяет свою скорость. На графике (рис. 1.3.2) это происходит в моменты времени t ₁ = –3 с , t ₂ = 4 с , t ₃ = 7 с и t ₄ = 9 с . По графику движения нетрудно найти, что на интервале ( t ₂; t ₁ ) тело двигалось со скоростью υ₁₂ = 1 м/с , на интервале ( t ₃; t ₂ ) – со скоростью υ₂₃ = –4/3 м/с и на интервале ( t ₄; t ₃ ) – со скоростью υ₃₄ = 4 м/с .

Следует отметить, что при кусочно-линейном законе прямолинейного движения тела пройденный путь l не совпадает с перемещением s . Например, для закона движения, изображенного на рис. 1.3.2, перемещение тела на интервале времени от 0 с до 7 с равно нулю ( s = 0 ). За это время тело прошло путь l = 8 м .

physics.ru

EasyFizika

Основное меню

Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти

Условие задачи:

Прямолинейное движение точки задано уравнением \(x=-2+3t-0,5t^2\) (м). Найти путь за 8 с.

Задача №1.3.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

В условии дано уравнение движения точки, давайте попробуем найти как меняется со временем её скорость. Это можно сделать двумя способами.

Первый способ — простой, его следует использовать, если вы не умеете брать производные от функций. В общем случае уравнение прямолинейного ускоренного движения точки выглядит так:

Мы же имеем такое уравнение:

Просто сопоставим эти уравнения. Тогда начальная координата \(x_0\), начальная скорость \(\upsilon _0\) и ускорение \(a\) в нашем случае равны:

Уравнение скорости в общем виде такое:

Подставив полученные нами значения, мы имеем такое уравнение скорости:

Суть второго способа заключается в том, что первая производная от функции координаты есть функция скорости.

\[\upsilon = ( — 2 + 3t — 0,5)’\]

Как видите, мы получили то же самое.

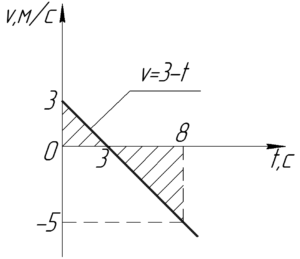Зная тот факт, что площадь фигуры под графиком зависимости скорости от времени есть пройденный путь, построим график \(\upsilon = 3 — t\) (рисунок справа). Получается, чтобы узнать путь \(S\) нужно посчитать площади двух треугольников и сложить их.

Кстати, расположение этих треугольников (над или под осью) также несет смысл. Если график скорости пересекает ось, значит тело меняет направление своего движения. Поэтому, в случае если мы ищем путь, по полученные площади необходимо сложить, если же мы пытаемся найти перемещение, то нужно отнять из большего меньшее.

Площадь прямоугольных треугольников определяется как половина произведения двух катетов, поэтому ответ такой:

\[S = \frac \cdot 3 \cdot 3 + \frac \cdot \left( \right) \cdot 5 = 17\; м\]

Наша точка прошла 4,5 м по оси \(x\) и 12,5 м против нее.

Ответ: 17 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок.

2 мысли о « Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти »

площадь прямоугольного треугольника=половине произведения двух катетов,но расчёт верный

easyfizika.ru

§ 7. Равномерное прямолинейное движение

При равномерном движении модуль скорости не изменяется: || = const, т.е. _t = 0.

При равномерном прямолинейном движении не изменяется ни модуль, ни направление скорости (таблица 1):

, т.е. _ср = _мгн = const.

Из формул (1, 2, 3) получим для равномерного прямолинейного движения:

вектор скорости , (13)

модуль скорости , (14)

проекция вектора скорости (на ОХ) . (15)

Из формулы модуля скорости (14) путь равномерного движения прямо пропорционален времени движения:

Из формулы (13) получим уравнение равномерного прямолинейного движения материальной точки:

(17)

Пример. При равномерном прямолинейном движении в положительном направлении оси ОХ (движение от начала отсчета) проекция вектора скорости – положительное число v_x > 0 (рис. 20). Уравнение движения и формула пути будут:

(18)

При равномерном прямолинейном движении в направлении, противоположном положительному направлению оси ОХ (движение к началу отсчета), проекция скорости – отрицательное число v_x 0

|₂| = const и v_2x 0 – то движение в положи-тельном направлении оси координат; если v_x 0.

Формула пути (14):

S₃ = v₃ (t – t₀₃) S = 2 м/с (t – 6 с) S = 2 м/с (8–6) с = 4 м.

Путь за 8 с равен: S = S₁ + S₃ = 8 (м).

Построим графики зависимости проекции скорости и пути от времени для этого движения.

1. Какое движение называется равномерным? равномерным прямоли-нейным?

2. Что характерно для равномерного движения? для равномерного пря-молинейного движения?

3. Какая зависимость пути и координаты при равномерном прямоли-нейном движении?

4. Напишите уравнение равномерного прямолинейного движения.

1. Скорость точки равна 72 км/ч. Выразить эту скорость в м/с.

2. Скорость точки равна 5 м/с. Выразить эту скорость в км/ч.

3. Две точки движутся по оси x.

Уравнения движения точек:

Построить графики зависимости координаты, пути и проекции скорости на ось х от времени: x_1,2(t); S_1,2(t); v_1,2(t).

4. Две точки движутся по оси х.

5. Дан график зависимости координаты движения точки от времени. Написать уравнения движения точки x(t) для интервалов времени:

t₁ [0; 2 с]

t₂ [2 с; 6 с]

t₃ [6 с; 8 с]

Построить график v_x(t), t [0; 8 с]. Найти путь и перемещение точки за интервал времени t I [0; 8 с].

6. Дан график зависимости проекции скорости на ось х от времени v_x(t).

Построить график зависимости координаты точки от времени x(t), если x₀ = 2 м и график зависимости пути от времени для интервала времени

t [0; 8 с].

Найти модуль перемещения точки за 8 с.

7. Тело движется равномерно под углом 30° к горизонту. Скорость тела 54 км/ч. На какую высоту поднимется тело за 30 секунд?

7.1 Примеры решения задач

(равномерное прямолинейное движение)

Задачи по кинематике (равномерное прямолинейное движение) можно решать аналитическим методом (применяя формулы данного движения табллица 2), графическим методом (надо знать графики простейших элементарных функций §7), координатным методом.

Для решения задач координатным методом следует (алгоритм решения):

– Выбрать тело отчета и связать с ним систему координат, направление осей координат, момент начала отчета времени.

Прямолинейное движение удобно рассматривать в системе координат, одну из осей которой лучше направить по направлению движения тела (или одного из тел).

– Сделать рисунок и проанализировать характер движения, кинематические характеристики движения.

– Записать уравнения равномерного прямолинейного движения, определяющие положение материальной точки в любой момент времени, в векторной записи (и в проекции на оси координат) – §7 (17).

– Решить полученное уравнение (или систему уравнений). Надо проверить равно ли число уравнений числу неизвестных.

– Задачу следует решать в общем виде, что позволяет проверить правильность решения.

Приступая к решению задач по данной теме повторите теорию §7 и тему «Векторы. Действия с векторами» – §18.

Две точки движутся по оси х.

Найти время и координату встречи. Сделать рисунок. Построить гра-фики S = S(t), x = x(t).

x₀₁ = 4 м; t₀₁ = 0; v_1x = 2 м/с, .

Построить графики x₁ = f(t) и x₂ = f(t)

Из второго уравнения запишем: x₀₂ = 11 м; t₀₂ = 0; v_2x = –5 м/с, .

Вывод:
1) первая точка движется равномерно прямолинейно в положительном направлении оси ОХ (от начала отсчета) (рис. 20).

2) вторая точка движется равномерно прямолинейно противоположно положительному направлению оси ОХ (к началу отсчета) (рис. 21).

Сделаем рисунок. Тела встречаются, и в момент встречи (т. С) их коор-динаты (расстояние от т. О) равны:

4 + 2t = 11 – 5t; 7t = 7; t_{встречи} = 1 (с).

Найдем координату места встречи (т. С): x₁ = 4 + 2t_{встречи}; x₁ = 4 + 2 • (1 c) = 6 (м), или x₂ = 11 – 5t_{встречи}; x₂ = 11 – 5 • (1 c) = 6 (м).

Итак, встреча произошла в т. С, расположенной от начала координат на расстоянии 6 м.

Построим графики x₁ = f(t) и x₂ = f(t) (§ 7).

web-local.rudn.ru

Графики равномерного прямолинейного движения (Колебошин С.В.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы узнаем, как графическим методом описать прямолинейное равномерное движение. Научимся строить график такого движения по закону или с помощью графика записывать закон движения. Также узнаем геометрический смысл графика зависимости проекции скорости от времени и решим несколько типовых задач на данную тему.

На прошлом уроке мы изучили прямолинейное равномерное движение (далее ПРД). На примере такого движения мы познакомимся и начнем работать с одним из способов изучения физических процессов – графическим способом. С таким способом представления информации мы хорошо знакомы: биржевые сводки (рис. 1), прогнозы погоды (рис. 2), инфографика (рис. 3).

Рис. 1. Биржевые сводки

Рис. 2. Прогноз погоды

Рис. 3. Инфографика

Работа с графиками очень удобна и полезна. Например, сравните данные о погоде на рис. 4 и рис. 5. С помощью графика можно мгновенно оценить, в какой день была самая высокая температура, самая низкая, одинаковая и т. д.

Рис. 4. Табличный способ задания температуры в каждый день недели

Рис. 5. Данные о температуре, заданные с помощью графика

[00:01:56Формулы для прямолинейного равномерного движения]

1. Проекция перемещения

2. Закон прямолинейного равномерного движения (зависимость координаты от времени)

В этих формулах значения величин (начальной координаты) и (проекции скорости) являются постоянными, а значения (перемещения), (координаты) и t (времени) – переменными.

Из курса математики нам известно уравнение, аналогичное . Это уравнение прямой (линейная зависимость):

Следовательно, графически обе зависимости будут выглядеть одинаково.

График зависимости перемещения от времени

Такой график проходит через начало координат и представляет собой график прямой пропорциональной зависимости. В зависимости от знака проекции скорости проекция перемещения возрастает или убывает со временем. На рисунке 6 для первого и второго тела проекция скорости больше нуля (у первого тела модуль скорости больше, так как больше наклон графика), для четвертого – меньше нуля. Для третьего тела проекция перемещения равна нулю, поэтому тело находится в состоянии покоя, проекция скорости равна нулю.

Рис. 6. График прямолинейного равномерного движения

Для ПРД путь всегда равен модулю перемещения, поэтому при проекции скорости, большей нуля, графики пути от времени и перемещения от времени совпадают (рис. 7а). Если проекция скорости меньше нуля, то график будет являться зеркальным отражением графика относительно оси времени (путь не может уменьшаться с течением времени) (рис. 7б).

Рис. 7а. График зависимости перемещения от времени и пути от времени при

Рис. 7б. График зависимости перемещения от времени и пути от времени при

График зависимости координаты от времени

График зависимости координаты от времени легко получить смещением графика вверх или вниз (в зависимости от знака начальной координаты ). На рисунке 8 показаны графики для нескольких движений, имеющих одинаковую скорость и различные координаты начальной точки: для первого тела – , для второго – , для третьего – , для четвертого – .

Рис. 8. График зависимости координаты от времени

При построении графиков в физике необходимо подписывать каждую ось не только символом той или иной физической величины, но и ее единицами измерения (рис. 9).

Рис. 9. Примеры оформления графиков в физике

Задача 1 (построение графика по уравнению движения)

Постройте графики движений, описываемых уравнениями: , .

Общий вид закона при ПРД:

Для первого движения:

— начальная координата ;

— проекция скорости .

Для второго движения:

— начальная координата ;

— проекция скорости .

Графики данных движений являются прямыми, поэтому для их построения нужны две точки. Одна точка – это начальная координата. Вторую точку найдем, подставив произвольный момент времени t в соответствующее уравнение движения.

Для первого тела возьмём 2 с:

м

Для второго тела возьмем :

м

Получили вторую точку, следовательно, можно строить графики движений (рис. 10).

1 – график движения, описываемый уравнением ;

2 – график движения, описываемый уравнением .

Рис. 10. Иллюстрация к задаче

Задача 2 (нахождение уравнения движения тела по графику )

По имеющимся графикам зависимости координаты от времени запишите уравнения движения тел (рис. 11). Определите графически время и место встречи тел. Проверьте полученный результат аналитически.

Рис. 11. Иллюстрация к задаче

Закон ПРД в общем виде:

1. Для каждого тела находим начальную координату и проекцию скорости.

Для первого тела:

;

Проекция скорости равна отношению перемещения ко времени:

Координату берем в произвольный и удобный для нас момент времени. Например, через 6 секунд () координата :

Следовательно, для первого тела уравнение движения выглядит так:

Для второго тела:

Через 2 секунды координата :

Для второго тела уравнение движения выглядит так:

2. Встреча двух тел – точка, в которой координаты тел одинаковые. На рисунке 12 видно эту точку. Опустим из нее перпендикуляры на ось времени (время встречи) и на ось координат (место встречи).

Рис. 12. Иллюстрация к задаче

Графически трудно определить точные числовые значения времени и места встречи. Приблизительно они равны:

Точные координаты можно определить аналитически. Так как координаты тел при пересечении совпадают, то , то есть можно приравнять уравнения движений:

Подставим данное значение времени встречи в любое уравнение движения, например во второе:

График зависимости проекции скорости от времени

ПРД можно охарактеризовать как движение с постоянной скоростью и по модулю, и по направлению, а это значит, что график проекции скорости от времени для такого движения будет представлять собой горизонтальную прямую. Например, графикам зависимости перемещения от времени на рисунке 6 соответствуют графики зависимости проекции скорости от времени на рисунке 13.

Рис. 13. Графики зависимости и для ПРД

Если в качестве положительного направления оси Х выбрать направление справа налево, то тогда первое и второе тело будет моделироваться движением легкового автомобиля (рис. 14), а движение четвертого тела будет моделироваться движением грузового автомобиля (его проекция скорости отрицательна). Третье тело находится в состоянии покоя.

Рис. 14. Моделирование движения первого, второго и четвертого тел

С помощью графика можно определять перемещение тела (геометрический смысл перемещения).

Пусть нас интересует перемещение тела за некоторое время t (рис. 15). Опустим перпендикуляр к оси абсцисс из соответствующей точки графика зависимости проекции скорости от времени. Рассмотрим полученный прямоугольник, его площадь равна произведению высоты на основание t:

Но произведение на t – это перемещение. Следовательно, площадь фигуры между графиком и осью абсцисс численно равна модулю перемещения тела.

Рис. 15. График зависимости

Пользуясь только графиком решить главную задачу механики невозможно (определить положение тела в любой момент времени), так как для этого необходимо знать начальную координату тела .

Задача 3 (построение графика по графику )

По имеющемуся графику зависимости проекции скорости от времени (рис. 16) постройте график зависимости координаты от времени, если известно, что тело начало свое движение из точки с координатой 2 метра.

Рис. 16. Иллюстрация к задаче

1. Определим уравнение движения тела.

Из графика видно, что тело движется равномерно прямолинейно. В общем виде закон ПРД выглядит так:

Начальная координата известна из условия . Из графика видно, что проекция скорости равна .

Следовательно, уравнение движения выглядит так:

2. Построим график движения для получившегося уравнения. График представляет собой прямую линию. Для ее построения необходимо 2 точки: одна точка нам известна – , вторую точку найдем, подставив произвольный момент времени t в соответствующее уравнение движения (рис. 17).

Рис. 17. Иллюстрация к задаче

Получили соответствующий графику график .

Итоги урока

На этом уроке мы научились описывать ПРД графическим методом. То есть, видя график такого движения, можем записать закон или, наоборот, по закону построить график. Мы узнали геометрический смысл графика зависимости проекции скорости от времени. Следовательно, мы изучили всё о ПРД и можем смело переходить к другим более сложным видам движения, так как в природе ПРД встречается крайне редко. Чаще всего, это неравномерное движение (рис. 18).

Рис. 18. Неравномерное движение

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
3. О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
4. А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Упражнение 1 (1, 2) стр. 22 – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы);
2. Что представляет собой график зависимости координаты тела от времени при равномерном прямолинейном движении?
3. Вдоль оси Ox движутся два тела, координаты которых изменяются согласно формулам: и . Как движутся эти тела? В какой момент времени тела встретятся? Найдите координату точки встречи.
4. Как по графику зависимости определяется перемещение тела при равномерном прямолинейном движении?
5. По графику движения тела (рис. 19) составить описание движения и записать уравнение движения этого тела.

   

   Рис. 19. Иллюстрация к задаче

   Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

   interneturok.ru