Идеальные газы. Законы идеального газа. Уравнение Менделеева — Клапейрона.

1. Идеальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.
2. Для идеальных газов справедливы следующие законы:

а) Закон Бойля — Mаpuomma: при неизменных температуре и массе произведение численных значений давления и объема газа постоянно:
pV = const

Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1).

б) Закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:
V = V0(1 + at)

где V — объем газа при температуре t, °С; V0 – его объем при 0°С. Величина a называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С–1). Следовательно,
V = V0(1 +(1/273)t)

Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к –273°С) закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

в) Закон Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре:
p = p0(1+gt)

где р0 — давление газа при температуре t = 273,15 К.
Величина g называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1. Таким образом,
p = p0(1 +(1/273)t)

Графическая зависимость давления от температуры изображается прямой линией – изохорой (Рис. 3).

г) Закон Авогадро: при одинаковых давлениях и одинаковых температурах и равных объемах различных идеальных газов содержится одинаковое число молекул; или, что то же самое: при одинаковых давлениях и одинаковых температурах грамм-молекулы различных идеальных газов занимают одинаковые объемы.
Так, например, при нормальных условиях (t = 0°C и p = 1 атм = 760 мм рт. ст.) грамм-молекулы всех идеальных газов занимают объем Vm = 22,414 л.· Число молекул, находящихся в 1 см3 идеального газа при нормальных условиях, называется числом Лошмидта; оно равно 2,687*1019> 1/см3
3. Уравнение состояния идеального газа имеет вид:
pVm = RT

где р, Vm и Т — давление, молярный объем и абсолютная температура газа, а R — универсальная газовая постоянная, численно равная работе, совершаемой 1 молем идеального газа при изобарном нагревании на один градус:
R = 8.31*103 Дж/(кмоль*град)

Для произвольной массы M газа объем составит V = (M/m)*Vm и уравнение состояния имеет вид:
pV = (M/m) RT

Это уравнение называется уравнением Менделеева — Клапейрона.
4. Из уравнения Менделеева — Клапейрона следует, чти число n0 молекул, содержащихся в единице объема идеального газа, равно
n0 = NA/Vm = p*NA /(R*T) = p/(kT)

где k = R/NA = 1/38*1023 Дж/град — постоянная Больцмана, NA — число Авогадро.

www.examen.ru

Объединение учителей Санкт-Петербурга

Основные ссылки

Уравнение состояния идеального газа. Газовые законы.

Уравнение состояния идеального газа

(уравнение Менделеева – Клапейрона).

Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.

В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеаль­ного газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.

В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.

Мы знаем, что 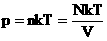. Следовательно, 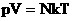. Учитывая, что 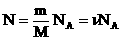, получим: .

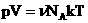Произведение постоянных величин есть величина постоянная, следовательно: 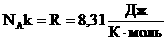— универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).

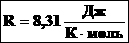
Таким образом, имеем:

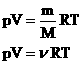— уравнение состояния (уравнение Менделеева – Клапейрона).

Другие формы записи уравнения состояния идеального газа.

1.Уравнение для 1 моля вещества.

Если n=1 моль, то, обозначив объем одного моля V_м, получим: .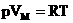

Для нормальных условий получим: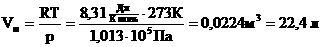

2. Запись уравнения через плотность: 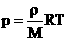— плотность зависит от температуры и давления!

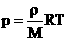
3. Уравнение Клапейрона.

Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: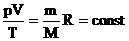

Эта запись означает, что для данной массы данного газа справедливо равенство: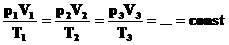

Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: .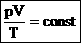

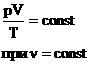
Газовые законы.

1. Закон Авогадро.

В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов).

Доказательство: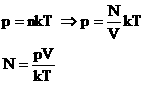

Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.

2. Закон Дальтона.

Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.

Доказательство: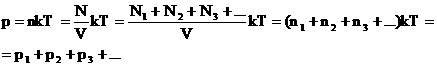

3. Закон Паскаля.

Давление, производимое на жидкость или газ, передается во все стороны без изменения.

www.eduspb.com

Законы идеального газа

Конспект лекции с демонстрациями

Аннотация: традиционное изложение темы, дополненное демонстрацией на компьютерной модели.

Из трех агрегатных состояний вещества наиболее простым является газообразное состояние. В газах силы, действующие между молекулами, малы и при определенных условиях ими можно пренебречь.

Газ называется идеальным, если:

— можно пренебречь размерами молекул, т.е. можно считать молекулы материальными точками;

— можно пренебречь силами взаимодействия между молекулами (потенциальная энергия взаимодействия молекул много меньше их кинетической энергии);

— удары молекул друг с другом и со стенками сосуда можно считать абсолютно упругими.

Реальные газы близки по свойствам к идеальному при:

— условиях, близких к нормальным условиям (t = 0 0 C, p = 1.03·10 5 Па);

— при высоких температурах.

Законы, которым подчиняется поведение идеальных газов, были открыты опытным путем достаточно давно. Так, закон Бойля — Мариотта установлен еще в 17 веке. Дадим формулировки этих законов.

Закон Бойля — Мариотта. Пусть газ находится в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими).Тогда для данной массы газа произведение давления на объем есть величина постоянная:

Эту формулу называют уравнением изотермы. Графически зависимость p от V для различных температур изображена на рисунке.

Свойство тела изменять давление при изменении объема называется сжимаемостью. Если изменение объема происходит при T=const, то сжимаемость характеризуется изотермическим коэффициентом сжимаемости который определяется как относительное изменение объема, вызывающее изменение давления на единицу.

Для идеального газа легко вычислить его значение. Из уравнения изотермы получаем:

Знак минус указывает на то, что при увеличении объема давление уменьшается. Т.о., изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления. С ростом давления он уменьшается, т.к. чем больше давление, тем меньше у газа возможностей для дальнейшего сжатия.

Закон Гей — Люссака. Пусть газ находится в условиях, когда постоянным поддерживается его давление (такие условия называются изобарическими). Их можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. Тогда изменение температуры газа приведет к перемещению поршня и изменению объема. Давление же газа останется постоянным. При этом для данной массы газа его объем будет пропорционален температуре:

где V₀ — объем при температуре t = 0 0 C, — коэффициент объемного расширения газов. Его можно представить в виде, аналогичном коэффициенту сжимаемости:

Графически зависимость V от T для различных давлений изображена на рисунке.

Перейдя от температуры в шкале Цельсия к абсолютной температуре , закон Гей — Люссака можно записать в виде:

Закон Шарля. Если газ находится в условиях, когда постоянным остается его объем (изохорические условия), то для данной массы газа давление будет пропорционально температуре:

где р₀ — давление при температуре t = 0 0 C, — коэффициент давления. Он показывает относительное увеличение давления газа при нагревании его на 1 0 :

Закон Шарля также можно записать в виде:

Закон Авогадро: один моль любого идеального газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях (t = 0 0 C, p = 1.03·10 5 Па) этот объем равен м -3 /моль.

Число частиц, содержащихся в 1 моле различных веществ, наз. постоянная Авогадро:

Легко вычислить и число n₀ частиц в 1 м 3 при нормальных условиях:

Это число называется числом Лошмидта.

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов, т.е.

где — парциальные давления — давления, которые бы оказывали компоненты смеси, если бы каждый из них занимал объем, равный объему смеси при той же температуре.

Уравнение Клапейрона — Менделеева. Из законов идеального газа можно получить уравнение состояния, связывающее Т, р и V идеального газа в состоянии равновесия. Это уравнение впервые было получено французским физиком и инженером Б. Клапейроном и российским учеными Д.И. Менделеевым, поэтому носит их имя.

Пусть некоторая масса газа занимает объем V₁, имеет давление p₁ и находится при температуре Т₁. Эта же масса газа в другом состоянии характеризуется параметрами V₂, p₂, Т₂ (см. рисунок). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического (1 — 1′) и изохорического (1′ — 2).

Для данных процессов можно записать законы Бойля — Мариотта и Гей — Люссака:

Исключив из уравнений p₁ ‘ , получим

Так как состояния 1 и 2 были выбраны произвольно, то последнее уравнение можно записать в виде:

Это уравнение называется уравнением Клапейрона, в котором В — постоянная, различная для различных масс газов.

Менделеев объединил уравнение Клапейрона с законом Авогадро. Согласно закону Авогадро, 1 моль любого идеального газа при одинаковых p и T занимает один и тот же объем V_m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. Тогда

Это уравнение и является уравнением состояния идеального газа, которое также носит название уравнение Клапейрона — Менделеева.

Числовое значение универсальной газовой постоянной можно определить, подставив в уравнение Клапейрона — Менделеева значения p, T и V_m при нормальных условиях:

Уравнение Клапейрона — Менделеева можно записать для любой массы газа. Для этого вспомним, что объем газа массы m связан с объемом одного моля формулой V=(m/M)V_m, где М — молярная масса газа. Тогда уравнение Клапейрона — Менделеева для газа массой m будет иметь вид:

где — число молей.

Часто уравнение состояния идеального газа записывают через постоянную Больцмана:

Исходя из этого, уравнение состояния можно представить как

где — концентрация молекул. Из последнего уравнения видно, что давление идеального газа прямо пропорционально его температуре и концентрации молекул.

Небольшая демонстрация законов идеального газа. После нажатие кнопки «Начнем» Вы увидите комментарии ведущего к происходящему на экране (черный цвет) и описание действий компьютера после нажатия Вами кнопки «Далее» (коричневый цвет). Когда компьютер «занят» (т.е. идет опыт) эта кнопка не активна. Переходите к следующему кадру, лишь осмыслив результат, полученный в текущем опыте. (Если Ваше восприятие не совпадает с комментариями ведущего, напишите!)

Вы можете убедиться в справедливости законов идеального газа на имеющейся компьютерной модели самостоятельными измерениями.

teachmen.ru

Газовые законы. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона, уравнение Клапейрона) — презентация

Презентация была опубликована 3 года назад пользователемТаисия Литвинова

Похожие презентации

Презентация на тему: » Газовые законы. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона, уравнение Клапейрона)» — Транскрипт:

2 Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона, уравнение Клапейрона)

3 Газовые законы- Количественные зависимости между двумя параметрами газа при фиксированном значении третьего

4 Изотермический процесс T=const Закон Бойля – Мариотта. Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется. В термостате pV = const p, V обратная пропорциональность

5 Изотермы Изотермическое расширение T = const p V V, p 1 2 T

6 Изотермы Изотермическое сжатие T = const p V V, p 2 1 T

8 Изобарный процесс p=const Закон Гей – Люссака. Для газа данной массы отношение объема газа к температуре постоянно, если давление газа не меняется. В цилиндре с подвижным поршнем V, T прямая пропорциональность

9 Изобары Изобарное расширение (нагревание) p = const p V V, T 12 T

10 Изобары Изобарное сжатие (охлаждение) p = const p V V, T 2 1 T

12 Изохорный процесс V=const Закон Шарля. Для газа данной массы отношение давления газа к температуре постоянно, если объем не меняется. В закрытом сосуде p, T прямая пропорциональность

13 Изохоры Изохорное нагревание V = const p V p, T 1 2 T

14 Изохоры Изохорное охлаждение V = const p V p, T 2 1 T

16 Закон Дальтона Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. ПАРЦИАЛЬНОЕ ДАВЛЕНИЕ – это такое давление, которое производил бы газ, если бы один занимал весь объем, равный объему смеси.

www.myshared.ru

Идеальный газ. Уравнение состояния идеального газа.Газовые законы;

Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.
Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. R = 8,31 Дж/моль • К.
Газовые законы– количественные зависимости между двумя параметрами, при фиксированном значении третьего параметра.

Процесс- это переход газа из одного состояния в другое.

Изопроцесс– процесс, в котором изменяются два параметра при неизменном третьем.

1. Изобарный процесс – процесс изменения состояния термодинамической системы протекающий при постоянном давлении(р=const) .Для него справедливо соотношение, вытекающее из уравнения состояния идеального газа. . 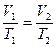или уравнение 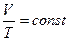,которое называется законом Гей-Люссака.

2. . Изохорный процесс – процесс изменения состояния термодинамической системы , протекающий при постоянном объеме(V=const).

3..Изотермический процесс— процесс, протекающий в системе с неизменной массой при постоянной температуре(T=const). Он описывается законом Бойля—Мариотта: РV =const

studopedia.su