Сложение чисел с разными знаками, правило, примеры.
В этой статье мы разберемся со сложением чисел с разными знаками. Здесь мы приведем правило сложения положительного и отрицательного числа, и рассмотрим примеры применения этого правила при сложении чисел с разными знаками.
Навигация по странице.
Правило сложения чисел с разными знаками
Положительные и отрицательные числа можно трактовать как имущество и долг соответственно, при этом модули чисел показывают величину имущества и долга. Тогда сложение чисел с разными знаками можно рассматривать как сложение имущества и долга. При этом понятно, что если имущество меньше долга, то после взаимозачета останется долг, если имущество больше долга, то после взаимозачета останется имущество, а если имущество равно долгу, то после расчетов не останется ни долга, ни имущества.
Объединим приведенные выше рассуждения в правило сложения чисел с разными знаками. Чтобы сложить положительное и отрицательное число, надо:
- найти модули слагаемых;
- сравнить полученные числа, при этом
- если полученные числа равны, то исходные слагаемые являются противоположными числами, и их сумма равна нулю,
- если же полученные числа не равны, то надо запомнить знак числа, модуль которого больше;
- из большего модуля вычесть меньший;
- перед полученным числом поставить знак того слагаемого, модуль которого больше.
- Плюс на минус дает минус;
- Минус на минус дает плюс.
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Озвученное правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшего числа. Также понятно, что в результате сложения положительного и отрицательного числа может получиться или положительное число, или отрицательное число, или нуль.
Также заметим, что правило сложения чисел с разными знаками справедливо для целых чисел, для рациональных чисел и для действительных чисел.
Примеры сложения чисел с разными знаками
Рассмотрим примеры сложения чисел с разными знаками по правилу, разобранному в предыдущем пункте. Начнем с простого примера.
www.cleverstudents.ru
Сложение и вычитание дробей
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
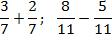
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
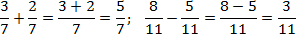
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
Разберем все это на конкретных примерах:
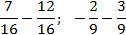
В первом случае все просто, а во втором внесем минусы в числители дробей:
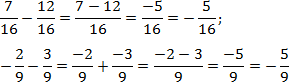
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
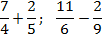
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
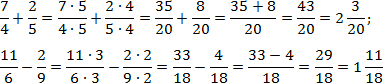
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
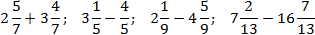
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
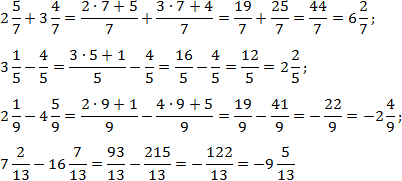
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
www.berdov.com
Сложение дробей с разными знаками правило
Действия с отрицательными и положительными числами
Абсолютная величина (модуль). Сложение.
Вычитание. Умножение. Деление.
Абсолютная величина ( модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
1) при сложении двух чисел с одинаковыми знаками складываются
их абсолютные величины и перед суммой ставится общий знак.
2) при сложении двух чисел с разными знаками их абсолютные
величины вычитаются ( из большей меньшая ) и ставится знак
числа с большей абсолютной величиной.
Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
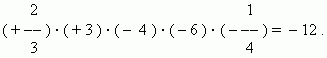
Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
www.bymath.net
Урок математики по теме «Сложение и вычитание чисел с разными знаками» (6-й класс)
Разделы: Математика
Цели и задачи урока:
- Обобщить и систематизировать знаний учащихся по данной теме.
- Развивать предметные и общеучебные навыки и умения, умение использовать полученные знания для достижения поставленной цели; устанавливать закономерности многообразия связей для достижения уровня системности знаний.
- Воспитание навыков самоконтроля и взаимоконтроля; вырабатывать желания и потребности обобщать полученные факты; развивать самостоятельность, интерес к предмету.
В результате этого урока учащиеся смогут:
- закрепить знания по темам: делимость чисел, обыкновенные дроби, отношения и пропорции, сложение и вычитание положительных и отрицательных чисел,
- активизировать внимание на различных этапах урока;
- научиться взвешивать и доказывать альтернативные мнения, принимать продуманные решения, общаться друг с другом;
Учебник: Математика. Учебник для 6 класса общеобразовательных учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.– М: “Русское слово”, 2009 г.
I. Вступительное слово учителя.
II. Проверка домашнего задания.
III. Повторение правил сложения и вычитания чисел с разными знаками. Актуализация знаний.
IV. Решение заданий по учебнику.
V. Самостоятельная работа по вариантам.
VI. Подведение итогов урока. Постановка домашнего задания.
- Компьютер
- Мультимедийный проектор, звуковые колонки
- Программа “Microsoft PowerPoint 2003” .Презентация.
- научить складывать отрицательные числа, числа с разными знаками и противоположные числа;
- развитие познавательной активности, творческих способностей, умения оценивать друг друга;
- формирование умения самостоятельно мыслить.
- 4 + 1,5 =
- 6,3 + 3,4 =
- 7,2 — 4,1 =
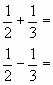
- 1,3 и 2,4;
- 3,15 и 3,17;
-
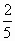 и
и 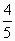 ;
; -
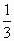 и
и 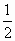 ;
; -
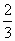 и
и 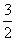 .
.
I. Организационный момент
Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.
xn--i1abbnckbmcl9fb.xn--p1ai
Сложение чисел с разными знаками. 6-й класс
Цели урока:
Ход урока
Устная работа: (приложение, слайд №2-4)
1. Как сложить две десятичные дроби?
(Сложение по разрядам, запятая — под запятой.)
2. Как сложить две обыкновенные дроби?
(- найти общий знаменатель;
— найти дополнительные множители;
3. Вычислить:
4. Как сравнить десятичные дроби? (по разрядам.)
5. Как сравнить обыкновенные дроби, если:
а) знаменатели равны; (из двух дробей с равными знаменателями больше та, числитель которой — больше)
б) числители равны; (из двух дробей с равными числителями больше та, числитель которой — меньше)
в) и числитель, и знаменатель — разные. (если числители и знаменатели дробей разные, то приводим их к общему знаменателю, а затем сравниваем их также как с равными знаменателями)
6. Сравнить:
7. Какие числа называются отрицательными? (числа со знаком «минус»)
8. Какие числа называются положительными? (числа со знаком «плюс»)
9. Какие числа называются противоположными? (числа, находящиеся на одинаковом расстоянии от нуля, но в противоположном направлении.)10. Назовите положительные, отрицательные и противоположные числа:
-5,2; 35; 7,8; 5,2; -19; 24; -1,7; 28,6; 19; 1/2; -16,7; 107; 293; -1/2; 25,6; 15,015; -3/4; 27 1/2; -5,2; 1/4; -35.
11. Когда возникли отрицательные числа? Где? Какие действия с ними умели выполнять древние? (приложение, слайд №5)
— Отрицательные числа появились приблизительно 2100 лет тому назад в Древнем Китае. Древние толковали о долге (отрицательные числа) и имуществе (положительные числа). Долгое время такие числа считали «несуществующими» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущество» или «долги», но как понимать произведение «имущества» и «долга»? Однако несмотря на такие сомнения и недоумения действия сложения, вычитания, умножения и деления выполнялись, правила для чего были предложены греческим математиком Диофантом еще в III в нашей эры.
Рассмотрим следующие задачи: (приложение, слайд № 6-10)
1. В книге доходов и расходов купца сделаны следующие записи:
