Правила алгебраической дроби

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень

Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень

Умножение алгебраических дробей осуществляется по тому же правилу, что и умножение обыкновенных дробей:

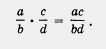
Аналогично обстоит дело с делением алгебраических дробей, с возведением алгебраической дроби в натуральную степень. Правило деления выглядит так:

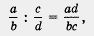
а правило возведения в степень

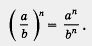
Прежде чем выполнять умножение и деление алгебраических дробей, полезно их числители и знаменатели разложить на множители — это облегчит сокращение той алгебраической дроби, которая получится в результате умножения или деления.

Пример 1. Выполнить действия:

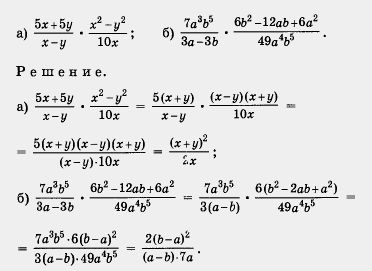
Воспользуемся тем, что (b — а) 2 = (а — b) 2 . Получим

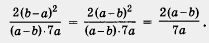
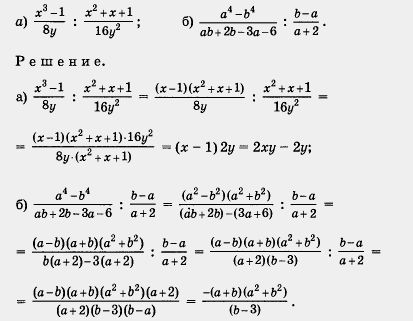
Мы учли, что в результате деления а — b на b — а получится -1.
Впрочем, знак «-» в данном случае лучше переместить в знаменатель:

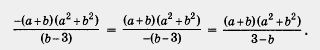
Пример З. Выполнить действия:

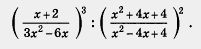
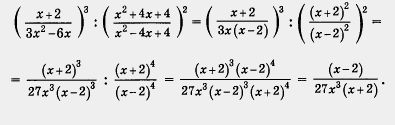
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Математика за 8 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

edufuture.biz

Алгебраические дроби. Сокращение алгебраических дробей

Прежде чем перейти к изучению алгебраических дробей рекомендуем вспомнить, как работать с обыкновенными дробями.

Любая дробь, в которой есть буквенный множитель, называется алгебраической дробью.

Примеры алгебраических дробей.

Как и у обыкновенной дроби, в алгебраической дроби есть числитель (наверху) и знаменатель (внизу).

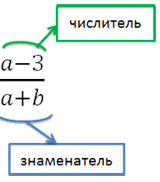
Сокращение алгебраической дроби

Алгебраическую дробь можно сокращать. При сокращении пользуются правилами сокращения обыкновенных дробей.

Напоминаем, что при сокращении обыкновенной дроби мы делили и числитель, и знаменатель на одно и тоже число.

Алгебраическую дробь сокращают таким же образом, но только числитель и знаменатель делят на один и тот же многочлен.

Рассмотрим пример сокращения алгебраической дроби.

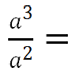
Определим наименьшую степень, в которой стоит одночлен « a » . Наименьшая степень для одночлена « a » находится в знаменателе — это вторая степень.

Разделим, и числитель, и знаменатель на « a 2 ». При делении одночленов используем свойство степени частного.

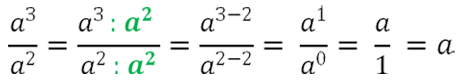
Напоминаем, что любая буква или число в нулевой степени — это единица.

Нет необходимости каждый раз подробно записывать, на что сокращали алгебраическую дробь. Достаточно держать в уме степень, на которую сокращали, и записывать только результат.

Краткая запись сокращения алгебраической дроби выглядит следующим образом.

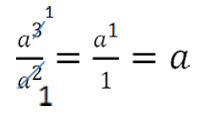
Сокращать можно только одинаковые буквенные множители.

Нельзя сокращать

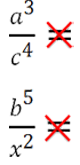
Можно сокращать

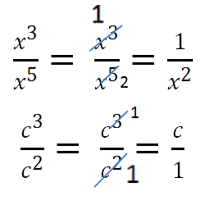
Другие примеры сокращения алгебраических дробей.

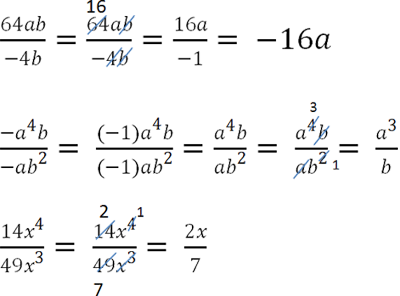
Как сократить дробь с многочленами

Рассмотрим другой пример алгебраической дроби. Требуется сократить алгебраическую дробь, у которой в числителе стоит многочлен.

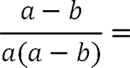
Сокращать многочлен в скобках можно только с точно таким же многочленом в скобках!

Ни в коем случае нельзя сокращать часть многочлена внутри скобок!

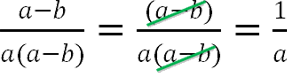
Определить, где заканчивается многочлен, очень просто. Между многочленами может быть только знак умножения. Весь многочлен находится внутри скобок.

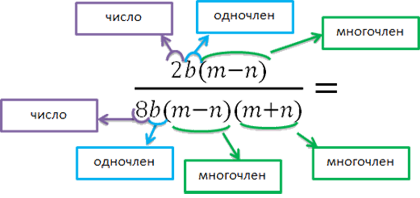
После того, как мы определили многочлены алгебраической дроби, сократим многочлен « (m − n) » в числителе с многочленом « (m − n) » в знаменателе.

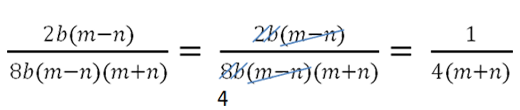
Примеры сокращения алгебраических дробей с многочленами.

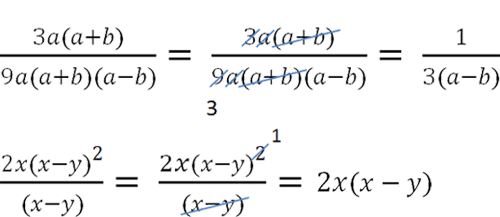
Вынесение общего множителя при сокращении дробей

Чтобы в алгебраических дробях появились одинаковые многочлены иногда нужно вынести общий множитель за скобки.

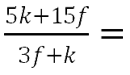
В таком виде сократить алгебраическую дробь нельзя, так как многочлен
« (3f + k) » можно сократить только со многочленом « (3f + k) ».

Поэтому, чтобы в числителе получить « (3f + k) », вынесем общий множитель « 5 ».

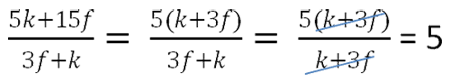
Сокращение дробей с помощью формул сокращенного умножения

В других примерах для сокращения алгебраических дробей требуется
применение формул сокращенного умножения.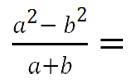

В первоначальном виде сократить алгебраическую дробь нельзя, так как нет одинаковых многочленов.

Но если применить формулу разности квадратов для многочлена « (a 2 − b 2 ) », то одинаковые многочлены появятся.

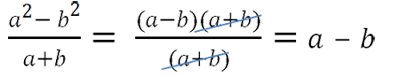
Другие примеры сокращения алгебраических дробей с помощью формул сокращенного умножения.

math-prosto.ru

Умножение алгебраических дробей

При умножении алгебраических дробей используют правила умножения обыкновенных дробей.

Правило умножения алгебраических дробей

При умножении алгебраических дробей
числитель умножается на числитель , а знаменатель — на знаменатель .

Рассмотрим пример умножения алгебраических дробей.

При сокращении алгебраических дробей используют правила сокращения алгебраических дробей.

Рассмотрим еще один пример умножения алгебраических дробей, которые содержат многочлены и в числителе, и в знаменателе.

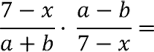
При умножении алгебраических дробей, которые содержат многочлены и в числителе, и в знаменателе, заключайте многочлены в скобки целиком.

Неправильно

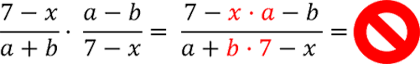
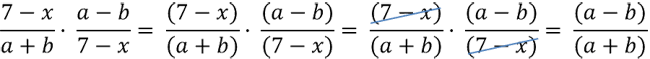
Как умножить алгебраическую дробь на одночлен (букву)

Рассмотрим пример умножения алгебраической дроби на одночлен.

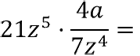
Представим одночлен « 21z 5 » как алгебраическую дробь со знаменателем « 1 ». Это можно сделать, так как при делении на « 1 » получается тот же самый одночлен.

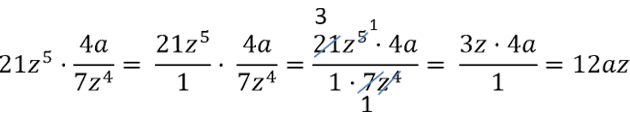
При умножении алгебраической дроби не забывайте использовать правило знаков.

Рассмотрим пример умножения двух отрицательных алгебраических дробей.

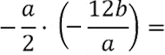
Перед тем как перемножить алгебраические дроби, определим итоговый знак по правилу знаков: « минус на минус дает плюс ».

Значит, итоговым знаком произведения будет знак « + ».

Методическая разработка по теме «Алгебраические дроби». 7-й класс

Разделы: Математика

Данный урок проводился в конце изучения темы “Алгебраические дроби” с целью повторения и закрепления знаний основных алгоритмов преобразований и действий с алгебраическими дробями.

Тема методической разработки.

Методика организации урока обобщения и систематизации знаний в соответствии с требованиями новых ФГОС.

Цели методической разработки.

Использование различных видов деятельности учащихся, применение элементов современных педагогических технологий (метапредметной технологии, технологии разноуровневого обучения, проблемно-развивающего обучения, коллективной работы, работы в парах).

Методическое обоснование темы.

Изучение темы “Алгебраические дроби” вызывает затруднения у многих учащихся, особенно, сложение и вычитание алгебраических дробей. Умение выполнять преобразования с алгебраическими дробями предполагает наличие знаний и умений учащихся по предыдущим темам, изучаемым в 7-м классе: “Алгебраические выражения”, “Одночлены и многочлены”, “Разложение многочлена на множители”, а также правил действия с обыкновенными дробями и др.

Решение многих теоретических и практических задач сводится к составлению математических моделей в виде алгебраических выражений, включающих алгебраические дроби. Приобретая опыт работы с такими моделями, учащиеся могут использовать этот опыт при изучении других предметов в школе и в практической жизни.

Сложность данной темы и ее важность для развития метапредметных умений учащихся очевидны и требуют особенно внимательного подхода к ее изучению с учетом введения в школе новых образовательных стандартов.

Методические рекомендации по проведению урока.

На изучение темы “Алгебраические дроби” по учебнику Алимова Ш.А по программе выделяется 22 часа. Из них 5 часов – на тему “Совместные действия с алгебраическими дробями”. Рассматриваемый урок рекомендуется проводить в завершение изучения данной темы перед контрольной работой.

Учитывая математическую подготовленность класса, можно варьировать объем самостоятельной работы учащихся, допуская повторение изученных алгоритмов действий с алгебраическими дробями по учебнику.

Тема урока: “Алгебраические дроби”

Тип урока: Урок повторения, систематизации и обобщения знаний, закрепления умений.

Вид урока: Урок-соревнование.

Формы работы на уроке: Коллективная, индивидуальная, в парах, в диалоге.

Цель методическая: Более глубокое усвоение, обобщение и систематизация знаний по теме “Алгебраические дроби” для обеспечения возможности их осмысленного использования учащимися вне урока математики.

• Обучения: Закрепление знаний, отработка навыков использования формул сокращенного умножения, приемов разложения многочленов на множители, правил преобразования, совместных действий над алгебраическими дробями. Обобщение материала по теме.
• Развития: Создание условий, обеспечивающих активную познавательную позицию учеников на уроке путем использования различных видов опроса, самостоятельной работы, межпредметной связи, развитие умений объяснять особенности, закономерности, анализировать, сопоставлять, сравнивать.
• Воспитания: Воспитание самооценки, самоконтроля в ходе самостоятельного выбора уровня сложности заданий. Воспитание общей культуры труда.

Материально-техническое обеспечение урока: карточки с разноуровневыми заданиями, жетоны (синие – 1 балл, зеленые – 2 балла, красные – 3 балла), компьютерная техника (компьютер, мультимедийный проектор, мобильный экран).

• Постановка цели урока и мотивация учебной деятельности учащихся (презентация учителя).
• Воспроизведение и коррекция опорных знаний по теме “Алгебраические дроби”, включающей операции сокращения, сложения и вычитания, умножения и деления алгебраических дробей, а также совместные действия с алгебраическими дробями. Сопоставление алгоритмов действий с обыкновенными и алгебраическими дробями. Решение заданий различной степени сложности.
• Релаксационная пауза (включается в ход урока после повторения темы “Сложение и вычитание алгебраических дробей”).
• Решение задачи, показывающей межпредметную связь.
• Подведение итогов урока.
• Домашнее задание.

1. Вступительное слово учителя

Сегодня на уроке мы повторим большую тему “Алгебраические дроби”, подготовимся к контрольной работе и постараемся понять, зачем нам нужны знания по данной теме.

Наш урок пройдет в виде соревнования за личное первенство. В ходе работы на уроке каждый из вас может “заработать” баллы за правильно выполненные задания, ответы и получить соответствующую оценку.

Давайте попытаемся ответить на вопросы:

• Что такое алгебраическая дробь?
• Какие операции производят с алгебраическими дробями?
• Математическая модель. Что это такое?
• Где используются алгебраические дроби?

Учащиеся отвечают на вопросы.

Правильно оценить ответы нам поможет презентация учителя “В мире алгебраических дробей” (Приложение 1).

Какой выводы мы можем сделать после просмотра презентации?

Учащиеся высказывают свои мнения.

• Алгебраические дроби используются не только на уроках математики, но и во многих сферах деятельности человека.
• Для применения алгебраических дробей необходимо научиться правильно оперировать ими: выполнять сокращение, сложение, вычитание, умножение, деление.

2. Повторение темы: “Алгебраическая дробь. Сокращение алгебраических дробей”.

2.1. Дифференцированный опрос у доски по карточкам:



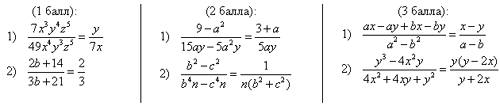
2.2. Во время подготовки отвечающих у доски – фронтальный опрос (за каждый правильный ответ – 1 балл):

• Дать определение алгебраической дроби.
• Как найти ее числовое значение?
• Любое ли значение могут принимать буквы, входящие в алгебраическую дробь?
• В чем заключается основное свойство дроби?
• Что значит сократить обыкновенную дробь?
• Что значит сократить алгебраическую дробь?
• Отличаются ли правила сокращения обыкновенных и алгебраических дробей?
• Какие способы разложения многочлена на множители вы знаете?

Учитель подводит итог:

Правила сокращения обыкновенных и алгебраических дробей аналогичны.

2.3. Слушаем, дополняем пояснениями, оцениваем ответы учеников, стоящих у доски.
За правильные дополнительные ответы учащиеся получают жетоны (баллы).



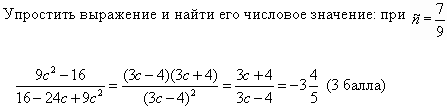
Проверку правильности решения делают учащиеся, работая в парах.

3. Повторение темы: “Сложение и вычитание алгебраических дробей”

3.1. Индивидуальный дифференцированный опрос по карточкам на доске. Выбор сложности задания осуществляется по желанию. Время выполнения – 10 минут.



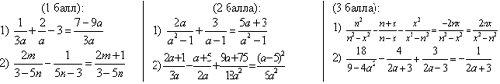
Ответы появляются на мобильном экране позже (во время проверки).

3.2. Во время подготовки учащихся по карточкам класс пишет диктант. Диктант составлен из выполненных упражнений. Задания предъявляются на мобильном экране (ответы – позже). В решении некоторых из них допущены ошибки. Выполненные задания записать в тетрадь. Если задание выполнено правильно, давать краткий ответ: “Да”, если неправильно: “Нет”. Выделять место появления ошибки (карандашом).



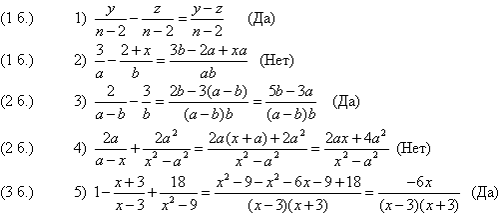
Проверку правильности решения делают учащиеся, работая в парах. Правильные ответы объявляет учитель.

3.3. Слушаем, дополняем, комментируем ответы учеников, выполняющих задания на доске. Повторяем правила сложения и вычитания алгебраических дробей. За правильные дополнения учащиеся получают жетоны (баллы).

Вопрос: Что вы можете сказать, сравнив правила сложения обыкновенных и алгебраических дробей?

Ответ: Да, правила сложения обыкновенных и алгебраических дробей аналогичны.

4. Релаксационная пауза.

Выполняем упражнения для расслабления глаз. Сядьте прямо. Прикройте глаза ладонями, опустите веки. Попытайтесь вспомнить что-нибудь приятное, например, море, звездное небо, речную гладь. Даже за 15–30 секунд ваши глаза немного отдохнут.

5. Повторение темы: “Умножение и деление алгебраических дробей”.

5.1. Индивидуальный дифференцированный опрос по карточкам:



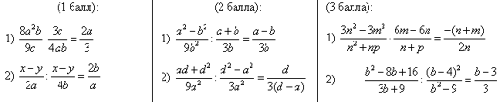
Примеры под цифрой 1) предложить для решения у доски, под цифрой 2) – самостоятельно, выбирая по желанию один пример из трех.

Слушаем, дополняем, комментируем ответы учеников, выполняющих задания на доске. За правильные дополнения учащиеся получают жетоны (баллы).

5.2. Перекрестный опрос:

• Правило умножения алгебраических дробей (1 балл).
• Правило деления алгебраических дробей (1 балл).
• Правило возведения в степень алгебраической дроби (1 балл).
• Правила умножения, деления, возведения в степень обыкновенных дробей.

Вопрос: Какой вывод вы можете сделать?

Ответ: Да, правила умножения и деления обыкновенных и алгебраических дробей аналогичны.

6. Повторение темы: “Совместные действия над алгебраическими дробями”.

Вопросы для повторения:

• Как устанавливается порядок действий в числовом выражении?
• Как устанавливается порядок действий в алгебраическом выражении?
• Какие способы записи решения при выполнении совместных действий над алгебраическими дробями вы знаете?

Предварительная работа – в парах, затем – фронтальный опрос.

Самостоятельная работа. Выполнить действия:

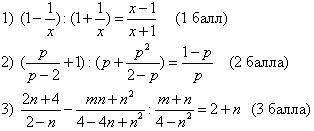
Время работы ограничено. Выбор заданий – по желанию, после предъявления правильных ответов учащиеся делают самопроверку самостоятельной работы.

7. Задача и учебника № 518 – как пример использования межпредметной связи.

Сопротивление R участка цепи, состоящего из двух параллельно соединенных проводников, вычисляется по формуле:

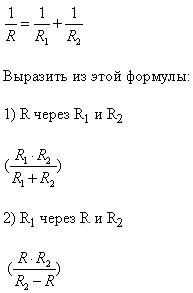
8. Подведение итогов:

• Каждый ученик самостоятельно подсчитывает число “заработанных” баллов, ставит себе оценку.

“5” – более 25 баллов
“4” – 20-25 баллов
“3” – 15-20 баллов

Тетради сдаются на проверку

• Целью нашего урока было не только повторение данной темы, но и возможность осмысленного применения полученных знаний на других уроках и в практической жизни.

9. Домашнее задание:

• Подготовьте карточки с заданиями на сокращение, сложение, вычитание, умножение, деление алгебраических дробей, совместные действия с алгебраическими дробями (для работы в парах на следующем уроке). Решите эти задания сами. Оцените степень их сложности по 3-бальной шкале.
• Подберите задачу, которую вы решали на уроке другого предмета или в практической жизни, решение которой содержит алгебраические дроби.

xn--i1abbnckbmcl9fb.xn--p1ai

Деление алгебраических дробей

Чтобы выполнить деление алгебраических (рациональных) дробей, надо

(Первую дробь умножаем на «перевернутую» вторую).

С помощью схемы деление алгебраических дробей можно изобразить так:



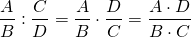
Рассмотрим примеры деления алгебраических дробей.



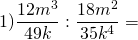
Чтобы разделить данные алгебраические дроби, нужно первую дробь умножить на дробь, обратную ко второй:



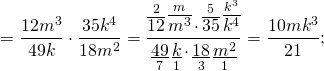
12 и 18 сокращаем на 6, 35 и 49 — на 7, m³ и m² — на m², k⁴ и k — на k.



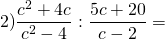
Деление алгебраических дробей заменяем умножением первой дроби на дробь, обратную второй:



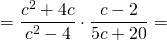
Входящие в состав дробей многочлены раскладываем на множители. У первой дроби в числителе выносим за скобки общий множитель c, знаменатель расписываем по формуле разности квадратов. У второй дроби в знаменателе выносим за скобки общий множитель 5:



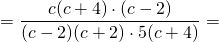
Сокращаем дробь на (c-2) и (c+4):





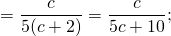
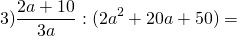
Первую дробь умножаем на дробь, обратную ко второй:



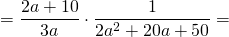
В числителе первой дроби выносим за скобки общий множитель 2, в знаменателе — аналогично:



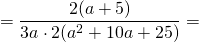
В знаменателе в скобках — полный квадрат суммы:



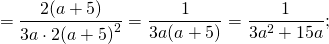
Сокращаем дробь на 2 и (a+5).



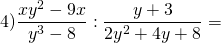
Деление алгебраических дробей заменяем умножением первой дроби на дробь, обратную ко второй:



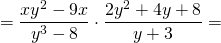
В числителе из первых скобок выносим общий множитель x, из вторых — 2. В знаменателе выражение, стоящее в первых скобках, раскладываем по формуле разности кубов:



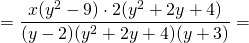
Сокращаем дробь на (y²+2y+4). Выражение y²-9 раскладываем на множители по формуле разности квадратов, после чего сокращаем дробь на (y+3):



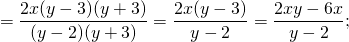
Правило деления алгебраических дробей можно использовать и при деление многочленов (впрочем, можно сразу заменить знак деления дробной чертой).

www.algebraclass.ru