Правила округление дробей

Округление натуральных чисел

Под округлением натурального числа понимают замену его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Правило округления:

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Цифра, записанная в выбранном разряде:

• увеличивается на единицу, если следующая за ней справа цифра — 5,6,7,8 или 9.

Все цифры, стоящие справа от данного разряда, заменяются нулями.

Пример: 143 ≈ 140 (округление до десятков);
5671 ≈ 5700 (округление до сотен).

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра в соседнем старшем разряде (слева) увеличивается на 1.

Пример: 796 ≈ 800 (округление до десятков);
970 ≈ 1000 (округление до сотен).

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление. Цифра, записанная в данном разряде:

• не меняется, если следующая за ней справа цифра — 0, 1, 2, 3 или 4;

Все цифры, стоящие справа от данного разряда, заменяются нулями. Если эти нули находятся в дробной части числа, то их не пишут.

Пример: 143,64 ≈ 143,6 (округление до десятых);
5,687 ≈ 5,69 (округление до сотых);
27,945 ≈ 28 (округление до целых).

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра в предыдущем разряде (слева) увеличивается на 1.

Пример: 89,6 ≈ 90 (округление до десятков);
0,097 ≈ 0,10 (округление до сотых).

files.school-collection.edu.ru

Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».

Приближённые значения

Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.

Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.

Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».

В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:



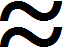
Читается как «приблизительно равно».

Чтобы указать приблизительное значение чего-либо, прибегают к такой операции, как округление чисел.

Округление чисел

Для нахождения приближенного значения применяется такая операция, как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулем. Например, следующие числа являются круглыми,

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числа.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, от нас требуют найти ближайшее круглое число для числа 17. При этом, в ходе этого поиска возможно изменения коснутся и цифры, которая находится в разряде десятков в числе 17 (т.е единицы).

Представим, что все числа от 10 до 20 лежат на прямой линии:



На рисунке видно, что для числа 17 ближайшее круглое число это 20. Значит ответ к задаче таким и будет: 17 приблизительно равно 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова представим, что все числа от 10 до 20 лежат на прямой линии:



На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приблизительно равно 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так случилось мы рассмотрим позже.

Попробуем найти ближайшее число для числа 15. Снова представим, что все числа от 10 до 20 лежат на прямой линии:



На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать большее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

Округлять можно и большие числа. Естественно, для них рисовать прямую линию и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:



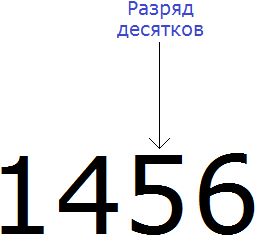
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56



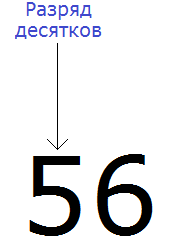
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60



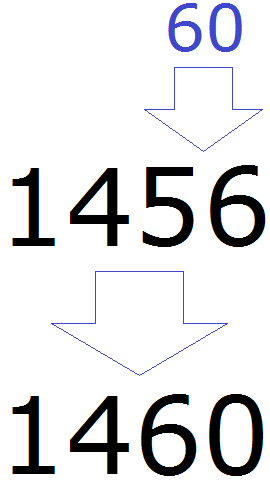
Значит при округлении числа 1456 до разряда десятков получим 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самого разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять можно также до разряда сотен, тысяч, десятков тысяч.

После того, как становится понятно, что округление это ни что иное, как поиск ближайшего числа, можно применять готовые правила, которые значительно облегчают округление чисел.

Первое правило округления

Из предыдущих примеров стало ясно, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.

Первое правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Например, округлим число 123 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.

Видим, что в разряде десятков находится двойка. Значит сохраняемой цифрой является цифра 2



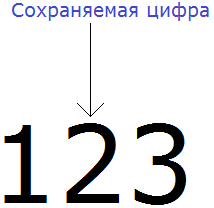
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.



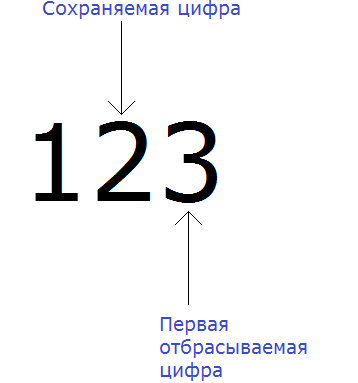
Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):

Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.

Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.

Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.



Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:



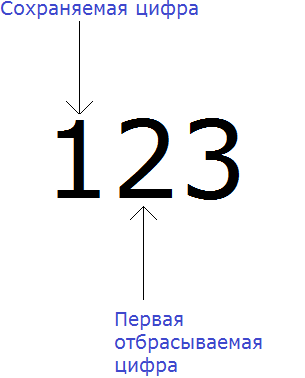
Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:

Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.

Пример 3. Округлить число 1234 до разряда десятков.

Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:

Пример 4. Округлить число 1234 до разряда сотен.

Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:

Пример 3. Округлить число 1234 до разряда тысяч.

Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:

Второе правило округления

Второе правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Например, округлим число 675 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.

Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7



Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.



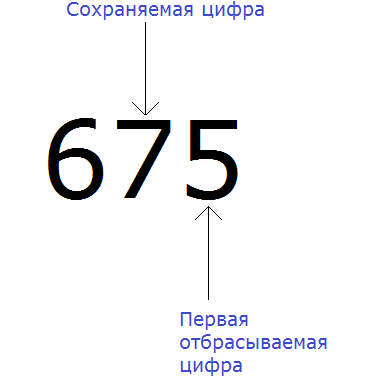
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:

Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.

Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.

Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:



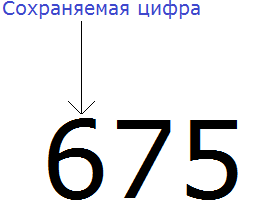
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:



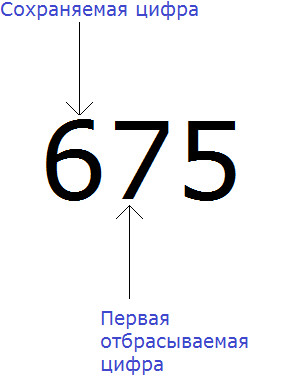
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:

Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.

Пример 3. Округлить число 9876 до разряда десятков.

Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:

Пример 4. Округлить число 9876 до разряда сотен.

Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:

Пример 5. Округлить число 9876 до разряда тысяч.

Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:

Пример 6. Округлить число 2971 до сотен.

При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.

В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:



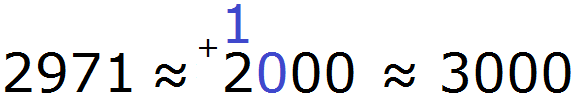
Округление десятичных дробей

При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:

Разряды целой части:

• разряд единиц
• разряд десятков
• разряд сотен
• разряд тысяч

Разряды дробной части:

• разряд десятых
• разряд сотых
• разряд тысячных

Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:



Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.

Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.

Мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3



Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):

Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:



Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:

Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:

123,456 ≈ 123,0 ≈ 123

Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:



Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями

Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:



Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

spacemath.xyz





В практической деятельности человека бывают числа двух видов: точные и приближённые . Часто знание лишь о приближённом числе достаточно для понимания сути дела. Иногда употребляют приближённые числа, так как точное не требуется, а иногда точное число невозможно найти в принципе.

У треугольника 3 стороны. Число 3 – точное.

Сколько учеников в вашей школе? Вряд ли кто-нибудь, кроме директора, ответит точно на этот вопрос. Ученик же посчитает так: 20 классов примерно по 25 человек, получится примерно 500. Если спрашивающего устраивает такая точность, можно считать, что мы получили хорошее приближение.

В приближённых вычислениях часто приходится округлять как точные, так и приближённые числа. Под округлением понимают отбрасывание одной или нескольких последних цифр в десятичном представлении числа. При округлении соблюдают следующие правила.

Если первая из отбрасываемых цифр больше 5, то последняя из сохраняющихся цифр увеличивается на 1. Если первая из отбрасываемых цифр равна 5, а за ней следуют одна или несколько значащих цифр, то последняя из сохраняющихся цифр также увеличивается на 1.

Округлить число 74,28 до десятых.

При округлении числа 74,28 до десятых следует написать 74,3. Действительно, за цифрой 2, обозначающей разряд десятых следует цифра 8, которая больше 5. Следовательно, цифру 2 нужно увеличить на 1. Получается, как и было сказано, 74,3.

Округлить число 74,253 до десятых.

При округлении числа 74,253 до десятых также следует написать 74,3. Действительно, за цифрой 2, обозначающей разряд десятых, следует цифра 5, причём за этой цифрой есть ещё одна значащая цифра. Следовательно, цифру 2 нужно увеличить на 1. Получается, как и было сказано 74,3.

Если первая из отбрасываемых цифр меньше 5, то последняя из сохраняемых цифр остаётся неизменной.

Округлить число 74,24 до десятых.

При округлении числа 74,24 до десятых следует написать 74,2. Действительно, за цифрой 2, обозначающей разряд десятых, следует цифра 4, которая меньше 5. Следовательно, цифру 2 нужно оставить без изменения. Получается, как и было сказано, 74,2.

Если отбрасывается цифра 5, а за ней нет и никогда не было значащих цифр, то последняя из сохраняемых цифр остаётся неизменной, если она чётная, и увеличивается на 1, если она нечётная.



Округлить до десятых число 74,25.

Так как отбрасывается цифра 5, а за ней нет значащих цифр, причём сохраняемая цифра 2 – чётная, то её нужно оставить без изменений. Окончательно: 74,2.

Округлить до десятых число 74,35.

Так как отбрасывается цифра 5, а за ней нет значащих цифр, причём сохраняемая цифра 3 – нечётная, то её нужно увеличить на единицу (до чётного числа). Окончательно: 74,4.

Замечание. Во многих практических задачах пользуются упрощёнными правилами округления, согласно которым цифра, если за ней стоят цифры 0, 1, 2, 3, 4, при округлении не изменяется и увеличивается на 1 в противоположном случае. Это правило немного отлично от строгого правила, приведённого в нашем курсе. Будьте внимательны при решении задач – следует пользоваться строгими правилами округления.

mathematics.ru

5.5.7. Округление чисел

Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения . Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.

Примеры.

Округлить до целых:

1) 12,5; 2) 28,49; 3) 0,672; 4) 547,96; 5) 3,71.

Решение. Подчеркиваем цифру, стоящую в разряде единиц (целых) и смотрим на цифру, стоящую за ней. Если это цифра 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения, а все цифры после нее отбрасываем. Если же за подчеркнутой цифрой стоит цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на единицу.

1) 1 2 ,5≈13;

2) 2 8 ,49≈28;

3) 0 ,672≈1;

4) 54 7 ,96≈548;

5) 3 ,71≈4.

Округлить до десятых:

6) 0, 246; 7) 41,253; 8 ) 3,81; 9) 123,4567; 10) 18,962.

Решение. Подчеркиваем цифру, стоящую в разряде десятых, а затем поступаем согласно правилу: все стоящие после подчеркнутой цифры отбросим. Если за подчеркнутой цифрой была цифра 0 или 1 или 2 или 3 или 4, то подчеркнутую цифру не изменяем. Если за подчеркнутой цифрой шла цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на 1.

6) 0, 2 46≈0,2;

7) 41, 2 53≈41,3;

8 ) 3, 8 1≈3,8;

9) 123, 4 567≈123,5;

10) 18, 9 62≈19,0. За девяткой стоит шестерка, поэтому, девятку увеличиваем на 1. (9+1=10) нуль пишем, 1 переходит в следующий разряд и будет 19. Просто 19 мы в ответе записать не можем, так как должно быть понятно, что мы округляли до десятых — цифра в разряде десятых должна быть. Поэтому, ответ: 19,0.

Округлить до сотых:

11) 2, 045; 12) 32,093; 13) 0, 7689; 14) 543, 008; 15) 67, 382.

Решение. Подчеркиваем цифру в разряде сотых и, в зависимости от того, какая цифра стоит после подчеркнутой, оставляем подчеркнутую цифру без изменения (если за ней 0, 1, 2, 3 или 4) или увеличиваем подчеркнутую цифру на 1 (если за ней стоит 5, 6, 7, 8 или 9).

11) 2, 0 4 5≈2,05;

12) 32,0 9 3≈32,09;

13) 0, 7 6 89≈0,77;

14) 543, 0 0 8≈543,01;

15) 67, 3 8 2≈67,38.

Важно: в ответе последней должна стоять цифра в том разряде, до которого вы округляли.

www.mathematics-repetition.com

Округление числа в Excel

Предположим, что вы хотите округлить число до ближайшего целого, так как десятичные значения вам не важны, или представить число в виде степени 10, чтобы упростить приблизительные вычисления. Существует несколько способов округления чисел.

Изменение количества знаков после запятой без изменения значения

Выделите ячейки, формат которых требуется изменить.

Чтобы после запятой отображалось больше или меньше знаков, на вкладке Главная в группе Число нажмите кнопку Увеличить разрядность или Уменьшить разрядность .

Во встроенном числовом формате

На вкладке Главная в группе Число щелкните стрелку рядом со списком числовых форматов и выберите пункт Другие числовые форматы.



В списке Категория выберите значение Денежный, Финансовый, Процентный или Экспоненциальный в зависимости от типа данных.

В поле Число десятичных знаков введите требуемое число знаков после запятой.

Округление числа вверх

Используйте функцию ОКРУГЛВВЕРХ. В некоторых случаях может потребоваться использовать функции ЧЁТН и НЕЧЁТ для округления вверх до ближайшего четного или нечетного числа.

Округление числа вниз

Округление числа до ближайшего значения

Округление числа до ближайшего дробного значения

Округление числа до указанного количества значимых разрядов

Значимые разряды — это разряды, которые влияют на точность числа.

В примерах этого раздела используются функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ. Они показывают способы округления положительных, отрицательных, целых и дробных чисел, но приведенные примеры охватывают лишь небольшую часть возможных ситуаций.

В приведенном ниже списке содержатся общие правила, которые необходимо учитывать при округлении чисел до указанного количества значимых разрядов. Вы можете поэкспериментировать с функциями округления и подставить собственные числа и параметры, чтобы получить число с нужным количеством значимых разрядов.

Округляемые отрицательные числа прежде всего преобразуются в абсолютные значения (значения без знака «минус»). После округления знак «минус» применяется повторно. Хотя это может показаться нелогичным, именно так выполняется округление. Например, при использовании функции ОКРУГЛВНИЗ для округления числа -889 до двух значимых разрядов результатом является число -880. Сначала -889 преобразуется в абсолютное значение (889). Затем это значение округляется до двух значимых разрядов (880). После этого повторно применяется знак «минус», что дает в результате -880.

При применении к положительному числу функции ОКРУГЛВНИЗ оно всегда округляется вниз, а при применении функции ОКРУГЛВВЕРХ — вверх.

Функция ОКРУГЛ округляет дробные числа следующим образом: если дробная часть больше или равна 0,5, число округляется вверх. Если дробная часть меньше 0,5, число округляется вниз.

Функция ОКРУГЛ округляет целые числа вверх или вниз аналогичным образом, при этом вместо делителя 0,5 используется 5.

В общем при округлении числа без дробной части (целого числа) необходимо вычесть длину числа из нужного количества значимых разрядов. Например, чтобы округлить 2345678 вниз до 3 значимых разрядов, используется функция ОКРУГЛВНИЗ с параметром -4: = ОКРУГЛВНИЗ(2345678,-4). При этом число округляется до значения 2340000, где часть «234» представляет собой значимые разряды.

Округление числа до заданного кратного

Иногда может потребоваться округлить значение до кратного заданному числу. Например, допустим, что компания поставляет товары в ящиках по 18 единиц. С помощью функции ОКРУГЛТ можно определить, сколько ящиков потребуется для поставки 204 единиц товара. В данном случае ответом является 12, так как число 204 при делении на 18 дает значение 11,333, которое необходимо округлить вверх. В 12-м ящике будет только 6 единиц товара.

Может также потребоваться округлить отрицательное значение до кратного отрицательному или дробное — до кратного дробному. Для этого также можно применять функцию ОКРУГЛТ.

support.office.com