I.1.4 ИДЕАЛЬНЫЙ ГАЗ. ГАЗОВЫЕ ЗАКОНЫ. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

В молекулярно – кинетической теории рассматривается идеализированная модель реальных газов – идеальный газ.

Идеальный газ – газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. У реальных газов молекулы испытывают силы межмолекулярного взаимодействия.

При взаимных столкновениях и соударениях со стенками сосуда молекулы идеального газа ведут себя как абсолютно упругие шары с диаметром 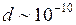м (эффективный диаметр молекулы), зависящим от химической природы газа. Наличие эффективного диаметра означает, что между молекулами действуют силы взаимного отталкивания. Межмолекулярные силы притяжения быстро убывают с увеличением расстояния 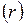между молекулами и не проявляются практически при 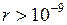м.

Существующие в действительности газы при не слишком низких температурах и достаточно малых давлениях – разреженные газы – по своим свойствам близки к идеальному газу. Например, гелий при комнатной температуре и атмосферном давлении с хорошим приближением подчиняется законам идеальных газов.

Опытным путем был установлен целый ряд законов, описывающих поведение идеальных газов.

Закон Бойля-Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная

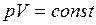. (I.3)

При ; .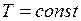

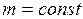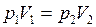. (I.4)

Изотерма – кривая, изображающая зависимость между величинам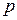и и 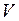, характеризующими свойства вещества при постоянной температуре. Изотермы представляют собой равнобочные гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (рис.1).

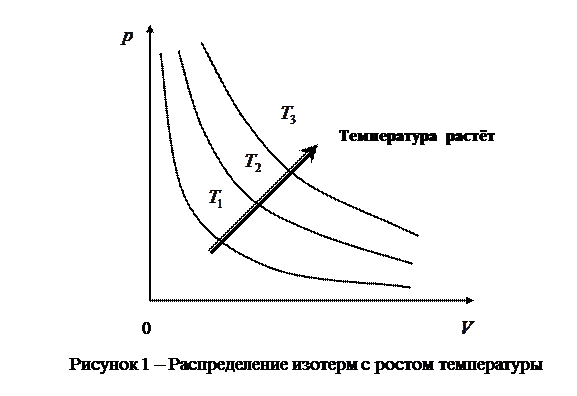
Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется линейно с температурой

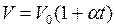. (I.5)

При ;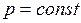

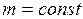
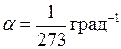(в СИ: 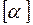= K –1 ).

Или другая форма записи закона

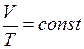. (I.6)

Для 2-х состояний

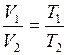. (I.7)

На диаграмме в координатах 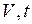(рис.2) этот процесс изображается прямой, называемой изобарой.

poznayka.org

Основы теплотехники

Основные законы теплотехники

Идеальные и реальные газы

Превращение теплоты в механическую работу в тепловых установках происходит при участии рабочего тела, которым обычно является газ или пар. Газы, которые существуют в природе, называют реальными . Молекулы этих газов имеют конечный объем, между ними существуют силы притяжения, существенно влияющие на их энергетические параметры.
Молекулы реального газа находятся в непрерывном хаотическом движении, т. е. обладают кинетической энергией движения. А поскольку между молекулами существует гравитационная, а зачастую и электромагнитная силовая связь, то они обладают и потенциальной энергией взаимодействия, которая зависит от расстояния между молекулами.

Для простоты изучения свойств газообразного рабочего тела введено понятие идеального газа – воображаемого газа, в котором молекулы рассматриваются, как материальные точки, обладающие некоторой массой, но силы взаимодействия между этими точками при анализе состояния рабочего тела и происходящих в нем процессов не учитываются.

При больших объемах и малых давлениях, когда расстояние между молекулами во много раз больше собственных размеров молекул, а также при высоких температурах, когда интенсивность хаотического движения молекул велика, и поэтому они слабо взаимодействуют между собой, складываются условия, при которых реальный газ можно с некоторым приближением считать идеальным.

Это позволяет вести расчеты для реальных газов по уравнениям и зависимостям, выведенным для идеальных газов, что упрощает сами расчеты и понимание сущности процессов, происходящих в газах. В связи с этим изучение термодинамических свойств идеальных газов имеет не только теоретическое, но и большое практическое значение.

Газовые законы термодинамики

Основными законами для идеальных газов, применяемыми в термодинамике, являются закон Бойля — Мариотта, закон Гей-Люссака, закон Шарля и закон Авогадро. Эти законы устанавливают зависимости между основными параметрами газов – давлением, объемом, температурой и молекулярной массой.
Впоследствии газовые законы, описывающие процессы в термодинамических системах с одним неизменным и двумя переменными параметрами газа, были объединены учеными Клайпероном и Менделеевым в уравнениях, описывающей процессы системы при всех переменных параметрах рабочего тела.

Закон Бойля — Мариотта

Закон Бойля — Мариотта утверждает, что произведение абсолютного давления газа на его удельный объем в изотермическом процессе (при постоянной температуре) есть величина постоянная:

Чтобы понять смысловую суть этого закона следует представить термодинамическую систему, состоящую из цилиндра с подвижным поршнем, заполненного в надпоршневом пространстве газом (рис. 1) . Система термоизолирована — тепло к ней не подводится и не отводится.
Тогда при очень медленном перемещении поршня влево или вправо будет уменьшаться или увеличиваться объем газа в цилиндре, при этом изменение объема приведет к обратно пропорциональному изменению давления. Т. е. при уменьшении объема в два раза, давление возрастет в два раза и т. п.
Очень медленное перемещение поршня в этом случае необходимо для того, чтобы не вызывать изменение температуры газа в процессе сжатия или расширения.

Закон справедлив для термодинамических систем с идеальным рабочим телом, в которых неизменным параметром является температура, а переменными — давление и объем. Подобные процессы (протекающие при постоянной температуре) называют изотермическими — абсолютная температура рабочего тела в системе постоянна.
Это не означает, что исключен подвод (или отвод) тепла к термодинамической системе в целом, однако тепловая энергия в этом случае не должна оказывать влияние на температуру газа (рабочего тела), а использоваться, например, для выполнения работы путем преобразования в другой вид энергии. Процессы, при которых полностью исключается подвод и отвод тепла к термодинамической системе носят название адиабатных процессов .

Закон Бойля — Мариотта — один из основных газовых законов, открытый в 1662 году английским ученым Робертом Бойлем. В 1676 году, независимо от выводов Р. Бойля, закон был вторично описан французским физиком Эдмом Мариоттом, поэтому носит двойное название по фамилиям авторов.

Закономерность, установленная Р. Бойлем и Э. Мариоттом, справедлива для идеальных газов, но может быть с высокой степенью точности применима и для разреженных газов. Для сжатых газов применение закона Бойля — Мариотта приводит к большим погрешностям.

Следует отметить, что применение закона Бойля — Мариотта, связывающего начальные и конечные величины давления и объёма газа друг с другом, не ограничивается изотермическими процессами. Он с достаточной степенью точности справедлив и в тех случаях, когда в ходе термодинамического процесса температура изменяется, но начальная и конечная температура газа в результате процесса оказываются равными.

Закон Гей-Люссака

Закон Гей-Люссака гласит, что при постоянном давлении (изобарный процесс) удельный объем газообразного вещества (объем постоянной массы газа) изменяется прямо пропорционально изменению абсолютных температур:

Для простоты рассмотрим, опять же, термодинамическую систему, состоящую из цилиндра с абсолютно подвижным (трение между стенками цилиндра и поршнем отсутствует) и невесомым поршнем. Над поршнем в цилиндре поместим газ.
Очевидно, что при нагреве газа поршень переместится в сторону увеличения объема газа. При этом изменение объема газа будет прямо пропорционально изменению его абсолютной температуры, поскольку мы исключили изменение давления за счет отсутствия сил трения и тяжести, действующих на поршень.

Закон носит имя одного из своих первооткрывателей — французского физика и химика Жозефа Луи Гей-Люссака, описавшего его в 1802 году. В разных источниках (особенно, зарубежных) этот закон нередко упоминается под названием закон Шарля, по имени француза Жака Шарля, который описал его в неопубликованной работе, датируемой 1787 годом.
Авторство приписывают, также, таким видным ученым конца XVII — начала XVIII века, как английский физик Джон Дальтон и французский ученый Гийом Амонтон.
В русскоязычных учебниках этот закон обычно называют по имени Гей-Люссака, который первым продемонстрировал его применимость ко всем газам, а также к парам летучих жидкостей при температуре выше точки кипения.

Закономерность, описанная Ж. Л. Гей-Люссаком, справедлива в системах с одним неизменным параметром — давлением, и переменными параметрами — температура — удельный объем. Такие термодинамические процессы (протекающие при постоянном давлении) называют изобарными (иногда — изобарическими) .

Закон Шарля

Закон Шарля, который иногда называют вторым законом Гей-Люссака, заключается в том, что при неизменном удельном объеме абсолютные давления газа изменяются прямо пропорционально изменению абсолютных температур:

Смысловое содержание закона Шарля проще понять, представив герметичный абсолютно жесткий сосуд, заполненный газом. Тогда при нагреве газа его давление будет увеличиваться прямо пропорционально увеличению абсолютной температуры, т. е. при увеличении абсолютной температуры в три раза, давление газа тоже возрастет в три раза и т. п.

Экспериментальным путем зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Жаком Шарлем, который исследовал термодинамические процессы имеющие место в идеальных газах.
Труды Шарля опубликованы не были, но его идеи были подхвачены видными физиками — Гей-Люссаком, Гильомом Амонтоном и другими, поэтому вопросы авторства некоторых основных законов термодинамики являются предметом спора между специалистами до сих пор.

Закономерность, открытая и описанная Ж. Шарлем, справедлива в системах с неизменным параметром — удельным объемом, и переменными параметрами — температура — давление. Такие термодинамические процессы (протекающие при постоянном объеме) называют изохорными (иногда — изохорическими) .

Закон Авогадро

Закон Авогадро утверждает, что все газы при одинаковом давлении и температуре содержат в равных объемах одинаковое число молекул. Из этого закона следует, что массы двух равных объемов различных газов с молекулярными массами μ₁ и μ₂ равны соответственно:

где: m₁ и m₂ – соответственно масса одной молекулы рассматриваемых газов; N – число молекул во взятом объеме.

Массы молекул пропорциональны молекулярным массам:

где z – коэффициент пропорциональности.

Тогда можно записать:

откуда получим пропорциональную зависимость:

Поскольку мы взяли равные объемы газов, то, разделив числитель и знаменатель левой части уравнения на объем, получим:

где: ρ₁ и ρ₂ – плотность рассматриваемых газов.

Так как удельный объем v является величиной, обратной плотности, т. е. v = 1/ρ , то можно записать полученную зависимость в следующем виде:

т. е. произведение удельного объема на молекулярную массу постоянно для любого газа при одинаковых условиях (давлении и температуре) .

Закон Авогадро можно сформулировать и так: объем киломоля различных газов при аналогичных физических условиях одинаков.

Этот закон был описан в 1811 году итальянским физиком Амедео Авогадро.

Закон Дальтона

Рабочее тело, используемое в термодинамических установках, обычно представляет собой смесь нескольких газов. Например, в двигателях внутреннего сгорания в состав продуктов сгорания, являющихся рабочим телом, входят водород, кислород, азот, окись углерода, углекислый газ, водяные пары воды и некоторые другие газообразные вещества.

В 1801 году английский физик Джон Дальтон установил закон, согласно которому давление, оказываемое смесью равно сумме парциальных давлений отдельных газов, входящих в состав смеси.
Парциальным давлением называют давление компонента смеси, которое он создавал бы, находясь один в занимаемой смесью объеме при температуре смеси.

Это утверждение легко доказать основываясь на выводах из закона Бойля — Маритта, рассматривая парциальные компоненты газовой по отдельности и в смеси.
Закон Дальтона применим для идеальных газов, и может быть использован для реальных газов, имеющих близкие к идеальным физические свойства и параметры.

Уравнение состояния газа

Газовые законы, описанные в начале статьи, справедливы для систем, в которых хотя бы один параметр рабочего тела в процессе остается неизменным. Такие процессы, в зависимости от того, какой из параметр постоянен, называют изотермическими, изобарными или изохорными.
На практике обычно приходится наблюдать термодинамические процессы, во время которых изменяются все основные параметры рабочего тела — политропные процессы .
Для описания политропных процессов учеными Клайпероном и Менделеевым были предложены уравнения состояния газа, полученные, на основе анализа рассмотренных ранее газовых законов Бойля-Мариотта, Гей-Люссака, Шарля и Авогадро.

Предположим, что 1 кг газа переходит из состояния, характеризующегося параметрами p₁ , v₁ , T₁ в другое состояние – с параметрами p₂ , v₂ , T₂ . Допустим, что этот переход происходит сначала при постоянной температуре Т₁ до промежуточного удельного объема v’ , а затем при постоянном давлении р₂ до конечного удельного объема v₂ .

Тогда по закону Бойля — Мариотта имеем:

Следующая часть процесса протекает при постоянном давлении, начинается параметрами газа p₂ , v’ , T₁ и заканчивается параметрами газа v₂ , T₂ и p₂ (последний параметр остался неизменным после первого перехода) . Тогда, в соответствии с законом Гей-Люссака, можно получить выражение при p = const:

Приравняв найденное выражение для v’ в первой и второй частях (переходах) процесса, получим:

Преобразовав это равенство, имеем:

На основании полученного в результате уравнения, можно сделать вывод, что отношение произведения абсолютного давления газа на его удельный объем к абсолютной температуре есть величина постоянная. Для 1 кг газа эту величину называют удельной газовой постоянной и обозначают R :

pv/T = R или pv = RT .

Полученное уравнение называют уравнением состояния идеального газа или уравнением Клайперона.
Впервые это уравнение предложил французский физик и инженер Бенуа Поль Эмиль Клайперон, который долгое время жил и работал в России. Исследуя известный термодинамический цикл Карно, Клайперон в 1834 году вывел уравнение состояния идеального газа, которое носит его имя.

Так как R – величина постоянная для каждого газа, можно определить любой основной параметр газа, если известны два других его параметра.
Удельные газовые постоянные для большинства известных газов приведены в соответствующих справочных таблицах. Так, например, удельная газовая постоянная кислорода равна 259,8 Дж/(кг×К), углекислого газа — 188,9 Дж/(кг×К) и т. п.

Уравнение Менделеева — Клайперона

Если обе части уравнения состояния идеального газа (уравнения Клайперона) умножить на массу газа М , получим следующее выражение:

или, учитывая, что произведение массы на удельный объем это полный объем газа: Mv = V , получим:

Заменив в полученном уравнении объем газа его молекулярным объемом Vμ , а массу газа – молекулярной массой μ , получим уравнение состояния для 1 киломоля газа:

Уравнение состояния идеального газа в таком виде предложил в 1874 году Д. И. Менделеев, и, поскольку оно является частным случаем уравнения Клайперона, то носит название уравнения Менделеева — Клайперона для идеального газа (иногда его называют уравнением Клайперона — Менделеева) .

Из уравнения Менделеева — Клайперона можно определить универсальную газовую постоянную:

При нормальных физических условиях величина универсальной газовой постоянной равна

Используя универсальную газовую постоянную, легко определить величину удельной газовой постоянной для любого газа по формуле:

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники»
(в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

k-a-t.ru

Идеальный газ газовые законы

Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.

1. Изохорический процесс. Закон Шарля. V = const.

Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:

При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.

График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ— и VT-диаграммах (рис. 1.6). Уравнение изохоры:

Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:

При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV— и РT-диаграммах (рис. 1.8).

Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.

Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT— и РT-диаграммах (рис. 1.10).

Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.

5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.

6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится N_A=6,02·10 23 молекул (число Авогадро).

7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:

При , давление смеси газов:

ens.tpu.ru

Справочник химика 21

Химия и химическая технология

Идеальный газ. Газовые законы и уравнение состояния. Реальные газы

Объединенный газовый закон (уравнение состояния идеального газа) РУ = КТ. Нормальные температура и давление. Идеальные и реальные газы. [c.113]

В условиях низких давлений и высоких температур свойства газов удовлетворительно описываются уравнением (4) состояния идеального газа. Когда же газ находится при высоких давлениях и низких температурах, свойства его не подчиняются уравнению (4) и сопутствующим ему газовым законам. В таких случаях для расчетов используют так называемые уравнения состояния реального газа. Наибольшее применение в технологических расчетах получило уравнение состояния, основанное на принципе соответственных состояний [c.28]

Такие газы, как водород, азот, кислород, так называемые действительные или постоянные газы, в обычных условиях приближаются к идеальным. Вообще при нормальных температурах и давлении отклонение от идеальных газов меньше у тех газов, у которых критическая температура очень низка, а критическое давление велико. Для таких газов почти полностью справедливо выражение рУ=сопз1. Реальные газы следуют этому закону приблизительно и то при низких давлениях. Для реальных газов уравнение состояния газа рУ==ЯТ является предельным, т. е. становится справедливым только при р—>-0. Причина отклонения реальных газов от законов газового состояния заключается в следующем. [c.51]

Поскольку закон Дальтона вытекает из представлений об идеальных свойствах газов, он приводит к таким же отклонениям от свойств реальных газов, как и уравнение состояния идеального газа. Однако для большинства газовых смесей при невысоких давлениях эти отклонения не слишком значительны. [c.163]

Идеальный газ. Газовые законы и уравнение состояния. Реальные газы [c.11]

Таким образом метод Льюиса позволяет сохранить для реальных систем (газовых смесей и растворов) форму уравнений, и в первую очередь закона действующих масс, выведенных для идеальных систем. В то же время этот метод не вносит в термодинамику каких-либо новых принципов. Он предлагает путь не преодоления трудностей, возникающих при изучении равновесий в реальных системах, а как бы обхода их стороной. Дело в том, что для нахождения летучестей, входящих в выражение (V.200), используются или какие-либо уравнения состояния реального газа, или непосредственно опытные данные р — V — Т. [c.161]

Идеальным условились считать газ, молекулы которого не имеют собственного объема и между ними нет никакого взаимодействия. Поскольку у реальных газов это не так, газовые законы, в том числе и уравнение состояния, для реальных газов не выполняются. Однако в условиях значительной разреженности газов, когда собственный объем молекул ничтожно мал по сравнению с объемом, занимаемым всем газом, уравнение состояния идеальных газов может с известным приближением применяться. Реально такое применение возможно при малых давлениях (не больше 100 кПа) и высоких температурах (выше критической температуры данного вещества). Тем не менее, поскольку свойства реальных газов отклоняются от свойств идеальных газов вполне закономерно, оказалось возможным ввести в уравнение состояния соответствующие поправки и приблизить его, таким образом, к реальным условиям. Так были получены уравнения состояния реальных газов (см. 111.12). [c.13]

Уравнения (10) и (11), строго говоря, действительны для идеальных газовых систем. Как известно, реальные газы только при низких давлениях в той или иной степени подчиняются законам идеальных газов и при повышенных давлениях дают резкие отклонения от них. Поэтому необходимо получить выражения для оценки равновесия химических реакций, учитывающие отклонения реальных газов от идеальных. Кроме того, реальные химические системы могут быть не только однофазными, они могут заключать в себе газовую, жидкостную и твердую фазы. Эти вопросы также требуют уточнения расчета систем, состоящих из различных фаз одного агрегатного состояния и из многих фаз различного агрегатного состояния. [c.25]

Реальные газы при небольших давлениях достаточно точно подчиняются характеристическому уравнению (7). При высоких давлениях учитывается объем, занятый молекулами газа, и влияние межмолекулярного притяжения. Поэтому основные газовые законы для реальных газов не действительны. Впервые отклонение свойств реального газа от идеального было установлено и объяснено М. В. Ломоносовым. Первое уравнение состояния реального газа было дано Д. И. Менделеевы.м. [c.11]

Рассмотренные выше газовые законы выведены для идеальных газов (молекулы — идеально упругие шары силы сцепления между ними отсутствуют собственным объемом они не обладают). Реальные газы, разумеется, лишены этих идеальных качеств, причем, чем ниже температура и чем выше давление, тем сильнее они отходят от идеала . Ван-дер-Ваальс (1878) вывел уравнение состояния реальных газов [c.290]

При исследовании газовых законов оказалось, что реальные газы могут давать значительные отклонения от величин, вычисляемых по уравнению состояния идеального газа. Так, согласно закону Бойля — Мариотта произведение объема газа на давление при данной температуре должно быть величиной постоянной (рУ = К). [c.22]

Описание газовых законов дополним рассмотрением уравнения состояния реальных газов, так как при значительном повышении давления (плотности) газа начинает сказываться влияние сил межмолекулярного взаимодействия и собственного объема молекул, которые, как мы знаем, в уравнении состояния идеального газа не учитываются (см. также 1.4). [c.18]

При выводе уравнения закона действующих масс в реальных системах, казалось бы, логично использовать тот же путь, что и для идеальных систем, привлекая при рассуждениях вместо уравнения состояния, справедливого для идеальных газов, уравнения для реальных газов. Этим путем в свое время пошел Ван-Лаар при исследовании состояния равновесия в реальных системах. Однако при таком рассмотрении равновесия встретились трудности, связанные в первую очередь с тем, что нет общего уравнения состояния для реальных газов, справедливого в широком интервале давлений. Если же при выводе уравнения для энергии Гиббса газовой смеси воспользуемся одним из приближенных уравнений состояния, например уравнением [c.270]

Приведенные выше простые выражения для химических потенциалов компонентов идеальных фаз получаются при условии, что к газовой фазе применимы законы идеальных газов, а конденсированная фаза представляет собой идеальную смесь. В практике эти условия удовлетворяются сравнительно редко. Если газовая фаза является реальным газом и к ней неприменимо уравнение Клапейрона — Менделеева, то для опреде.иения химических потенциалов нужно знать уравнение состояния этого газа. При этом расчет значения представляет определенные трудности. Чтобы упростить расчеты и сохранить для реальных газов форму уравнений, выведенных для идеальных газов, Льюис [5] ввел функцию /, названную летучестью и определяемую с помош,ью изобарного потенциала Z выражением [c.52]

Законы идеальных газов, следствия, вытекающие из этих законов, и уравнения состояния (1.15), (1.16) часто используют в различных технохимических расчетах. Однако хорошее совпадение вычисленных результатов с опытными данными наблюдается лишь в ограниченной области температур и давлений. Газы, находящиеся в условиях, для которых неприменимы законы идеальных газов и уравнения газового состояния (1.15), (1.16), называются реальными или неидеальными. Параметры состояния р, V, Т таких газов для 1 кмоль связаны между собой уравнением Ван-дер-Ваальса [c.15]

Чтобы обойти это затруднение, Г. Льюис (1901) предложил заменять в уравнениях термодинамики, описывающих равновесия для идеальных газовых систем, давления р на величину /, называемую летучестью газа, или фугитивностью. Этот прием позволяет связать найденные опытным путем свойства реального газа (отклонения его от идеального состояния) с его термодинамическими параметрами. Согласно методу Льюиса летучесть (фугитивность) представляет собой давление, формально исправленное так, что при данной температуре и данном объеме можно применять уравнения термодинамики идеальных газов к реальным газам. Например, уравнение закона действия масс [c.139]

Законы газового состояния справедливы только для идеального газа. Поэтому в технических расчетах, связанных. с реальными углеводородными газами, законы для идеального газа применяют в пределах давлений до 2—10 атмосфер (в зависимости от вида газа) и при температурах, превышающих 0° С. При более высоких давлениях или более низких температурах применяют либо уравнения, учитывающие объем, занимаемый молекулами, и силы взаимодействия между ними, либо вводят в уравнения для идеального газа опытные поправочные коэффициенты — коэффициенты сжимаемости газа. [c.39]

Отклонения газовой фазы от идеального состояния не дают полной картины отклонений реального раствора от закона Рауля, так как они имеют место также и при низких давлениях, когда пар приблилсается по своим свойствам к идеальному газу. Отсюда следует, что жидкая фаза (раствор) также является источником отклонений от этого закона. Отклонения, причиной которых является жидкая фаза, могут быть очень значительными даже при низких давлениях. Мерой этих отклонений служат коэффициенты у1 и уг в уравнениях активносги (12-34). Термодинамика показывает, что существует связь между коэффициентами у1 и у2 для обоих компонентов в данной системе. [c.601]

Это уравнение дает величину минимальной работы, потребной для сжатия идеального газа от объема до Ц. В действительности процесс сжатия всегда необратим и следовательно потребная работа больше этой минимальной. В случае когда реальный газ не следует с достаточным приближением законам идеального газового состояния, соотношение между Р и V сложно и меняется в зависимости от природы газа. Вычисление работы расширения или сжатия интегрированием в этом случае очень кропотливо и удобнее осуществляется графическим методом, который будет описан далее. [c.96]

Для реальных газов в обычных пределах температуры и давления это приблизительно справедливо, и та как реальные газы при низких давлениях подчиняются законам идеального газового состояния, то указанное уравнение достаточно точно для них в этих условиях. При высоких давлениях 7 зависит и от температуры и от давления, и кроме того реальные газы при этом уже заметно отступают от идеальных законов. Следовательно, вышеприведенное уравнение не может быть в этих условиях применено к ним с достаточной точностью. В этих случаях лучшие результаты дают графический метод и энтропийные диаграммы, описанные на стр. 109 и след. Значение Для различных газов см, стр, 38, [c.97]

Законы газового состояния справедливы только для идеального газа. Следовательно, в технических расчетах, связанных с реальными углеводородными газами, законы для идеального газа применяют только в пределах давления до 0,2—1,0 МПа (в зависимости от вида газа) и при температурах, превышающих О °С. При более высоких давлениях или более низких температурах либо применяют уравнения, учитывающие [c.54]

Г азы, находящиеся в условиях, для которых неприменимы законы идеальных газов и уравнение газового состояния (10), называются реальными или неидеальными. Параметры состояния р, V, Т таких газов для 1 кмоль связаны между собой уравнением Ван-дер-Ваальса [c.22]

В методе газового насыщения, впервые примененном Реньо в 1845 г. [84], поток инертного газа проходит сквозь вещество илн над ним С достаточно малой скоростью, обеспечивающей полное равновесное насыщение. Давление пара вычисляют, исходя из предположения, что отношение парциального давления пара к общему давлению равно отношению объема пара к общему объему смеси пара и инертного газа (закон Дальтона). Объем пара должен быть вычислен по газовым законам из веса испарившегося вещества, который обычно находится или конденсированием пара и взвешиванием конденсатора, или определением потери в весе жидкости в сатураторе. Ес.та нужно, вводится небольшая поправка на отклонение уравнения состояния пара от идеального. Таким образом, область применения метода ограничивается условием, что в паре не должна иметь место ассоциация в большинстве случаев это условие выполняется. Джери и Джиллеспи [85] предложили точный способ вычисления давления пара, определяемого методом газового насыщения. Эти авторы пользуются уравнением состояния реального газа Битти — Бриджмена. Если не вводить поправок на неидеаль-ность, то возможны большие ошибки например, для иода эта ошибка составляет 1,6%. Для ознаком.чения с деталями мы отсылаем читателя к оригинальной работе. Там же даны указания о проведении эксперимента . [c.385]

Люис и Рендалл [5] для учета влияния оишонений реальных газов от уравнения состояния идеальных газов ввели в обычные термодипамиче-ские соотношения, основанные на применении идеальных газовых законов, ряд формальных по существу факторов, позволяющих получить более точные результаты нри расчетах. [c.159]

Уравнения, описывающие различные газовые законы, представляют собой строгие математические выражения. Измерения объема, давления и температуры, более точные, чем проводились Бойлем и Гей-Люссаком, показывают, что газы лишь приближенно подчиняются этим уравнениям. Свойства газов значительно отклоняютск от так называемых идеальных свойств, когда газы находятся под высоким давлением или при температурах, близких к температурам кипения соответствующих жидкостей. Таким образом, газовые законы, вернее законы состояния идеального газа, достаточно точно описывают поведение реальных газов только при низких давлениях и при температурах, далеких от температуры кипения рассматриваемого вещества. В разд. 3-8 мы вновь обратимся к проблеме уточнения простого закона состояния идеального газа, с тем чтобы он мог правильнее учитывать свойства реальных, неидеальных газов. [c.132]

Как уже указывалось, законы газового состояния веществ справедливы для идеальных газов. Все существующие реальные газы более или менее отклоняются от идеальных газов. Такие газы, как водород, азот, кислород, так называемые действительные или постоянные газы, в обычных условиях приближаются к идеальным газам. Вообще при нормальных температурах и давлении отклонение от идеальных газов меньше у тех газов, у которых критическая температура очень низка, а критическое давление велико. Для таких газов почти полностью справедливо уравнение Р1 =сопз . [c.23]

Уравнение Ван-дер-Ваальса. При исследовании газовых законов в более широких границах давлений и температур оказалось, что реальные газы практически дают значительные отклонения от величин, вычисляемых по уравнению состояния идеальных газов. Так, согласно закону Бойля— Мариотта, произведение объема газа на соответствующее давление при данной температуре должно быть величиной постоянной рУ=сопз1). Между тем оказалось, что применимость закона Бойля—Мариотта с достаточной точностью возможна только при невысоких давлениях. При значительных давлениях наблюдаются большие отклонения. Например, для азота опытным путем найдено, что если при р 1 атм рУ=100, то при р= =431 атм рУ=127 (вместо 100, как это следовало бы по закону Бойля—Мариотта). [c.15]

Уравнение (3) известно под названием объединенного закона Дальтона — Рауля. Формулируется он так в состоянии равновесия парциальное давление любого компонента смеси в паровой (газовой) фазе равно парциальному давлению пу)ов того же. компонента над жидкостью. Эхо ацаадт, что, аадавшись едр де-ленными температурой и давлением, можно определить равновесный состав паровой и жидкой фаз. Все три закона выведены для идеальных газов. На прак-гаке же при нефтепереработке поведение реальных газов значительно отличается от поведения идеальных (более высокое давление). В этих случаях в формулы вместо значений давлений компонентов нужно подставлять значения их фугитивности. [c.81]

Можно найти известную аналогию в развитии теории растворов электролитов и теории газового агрегатного состояния. В том и другом случаях первоначально предполагалось, что система ведет себя подобно идеальной и что между образующимися частицами нет сил взаимодействия. Приложение полученных на основе таких представлений законов к реальным системам приводило к значительным расхождениям между теорией и опытом. В связи с этим для газов вместо простого уравнгния газового состояния рУ = ЯТ предлагались другие, более сложные, в которых так или иначе учитывались силы взаимодействия между частицами. Одним из них было уравнение Ван-дер-Ваальса [c.73]

Теория газообразного состояния. Важнейшая теоретич. модель газообразного состояния-идеал ьный газ, для к-рого энергия взаимод. между молекулами пренебрежимо мала по сравнению с кинетич, энергией их хаотич. (теплового) движения. Ур-ние состояния для л молей идеального Г., занимающего объем У при т-ре Т и давлении р, имеет вид рУ=пЯТ, где К = 8,31 ДжДмоль-К)-газовая постоянная (см. Клапейрона-Менделеева уравнение). Внутр. энергия 1 моля одиоатомиого идеального газа = 7а Д»я идеального Г. строго выполняются Бойля-Мариотта закон и Гей-Люссака законы-, для реальных Г. эти законы выполняются приближенно-тем лучше, чем дальше р и Т от критич. значений. [c.474]

Во многих случаях для реальных растворов наблюдаются отчетливые отклонения от закона Генри. Причиной этого являются отклонения от идеального состояния газа над раствором и самого раствора. Если откотонение наблюдается только в газовой фазе, то расхождения с законом Генри появляются при высоких давлениях. Парциальное давление газа над раствором будет зависеть тогда не только от концентрации раствора, но и от общего давления. Как известно из рассмотрения процесса дистилляции (гл. XII), в этом случае вместо закона Рауля (14-13) следует применять уравнение активности [c.743]

Смотреть страницы где упоминается термин Идеальный газ. Газовые законы и уравнение состояния. Реальные газы: [c.127] [c.10] [c.536] Смотреть главы в:

chem21.info