Пример закона исключения третьего в логике

Пример закона исключения третьего в логике

3. Закон исключенного третьего

Закон исключенного третьего связан с противоречащими суждениями. Он означает, что может быть лишь два противоречащих друг другу суждения, третьего быть не может. Отсюда и пошло название данного закона.

Если два суждения отрицают друг друга, одно что-либо утверждает, а другое противоречит существованию утверждаемого, можно говорить о том, что эти суждения являются противоречащими. Каждое из этих суждений является самостоятельным и рассматривается отдельно в силу того, что содержит информацию, отрицающую противное суждение. Рассмотрение их в этом плане производится для того, чтобы определить, какое из них истинно, а какое – ложно. Поскольку такие суждения полностью исключают друг друга, т. е. при истинности одного другое всегда является ложным, нет третьего варианта. То есть это означает, что отсутствует любое промежуточное состояние между истинностью и ложностью. Значит, не может быть третьего суждения относительно одного предмета, отражающего те же свойства, которые отражаются (утверждаются или отрицаются) двумя противоречащими суждениями.

Для более полного уяснения вопроса следует привести примеры. Для начала рассмотрим схематичные отражения противоречащих суждений: «Ни одно S не есть Р» и «Некоторые S есть Р»; «Все S есть Р» и «Некоторые S не есть Р»; «Это S есть Р» и «Это S не есть Р». Как можно заметить, все три приведенные пары суждений являются, соответственно, общими, частными и единичными, а также контрадикторными (т. е. типа A и не-А). Суждения «Юрий Гагарин является космонавтом, который первым полетел в космос» и «Юрий Гагарин не является космонавтом, который первым полетел в космос» – это противоречащие суждения.

При рассмотрении закона исключенного третьего всегда возникает вопрос о его различиях с законом непротиворечия. Это связано с тем, что в отношении рассматриваемых сейчас противоречащих суждений применяются оба эти закона. Однако между ними существует различие. Оно становится явным, если рассматривать контрарные (например, «Все люди имеют конечности» и «Ни один человек не имеет конечностей») суждения. В отношении них закон исключенного третьего не применяется.

www.e-reading.mobi

3. ЗАКОН ИСКЛЮЧЁННОГО ТРЕТЬЕГО

Закон исключённого третьего, как и закон противоречия, устанавливает связь между противоречащими друг другу высказываниями. Он утверждает: из двух противоречащих высказываний одно является истинным.

А или не-А. Например: «Аристотель умер в 322 г. до н.э. или он не умер в этом году», «Личинки мух имеют голову или не имеют её» и т.п. Само название закона выражает его смысл: дело обстоит так, как говорится в рассматриваемом высказывании, или так, как говорится в его отрицании, и никакой третьей возможности нет.

Как выразил эту мысль Аристотель: «…Не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать».

Человек говорит прозой или не говорит прозой, кто-то рыдает’ или не рыдает, собака выполняет команду или не выполняет её и т.п. — других вариантов не существует. Мы можем не знать, противоречива некоторая теория или нет, но на основе закона исключённого третьего ещё до начала исследования мы вправе заявить: она или непротиворечива или противоречива.

Этот закон с иронией обыгрывается в художественной литературе. Причина иронии понятна: сказать «Нечто есть или его нет», значит, ровным счётом ничего не сказать, и смешно, если кто-то этого не знает.

В «Мещанине во дворянстве» Ж.-Б.Мольера есть такой диалог:

Г-н Журден. …А теперь я должен открыть вам секрет. Я влюблён в одну великосветскую даму, и мне хотелось бы, чтобы вы помогли написать ей записочку, которую я собираюсь уронить к её ногам.

Учитель философии. Конечно, вы хотите написать ей стихи?

Г-н Журден. Нет, нет, только не стихи.

Учитель философии. Вы предпочитаете прозу?

Г-н Журден. Нет, я не хочу ни прозы, ни стихов.

Учитель философии. Так нельзя: или то, или другое.

Г-н Журден. Почему?

Учитель философии. По той причине, сударь, что мы можем излагать свои мысли не иначе, как прозой или стихами.

Г-н Журден. Не иначе, как прозой или стихами?

Учитель философии. Не иначе, сударь. Все, что не проза, то стихи, а что не стихи, то проза.

В известной сказке Л.Кэролла Белый Рыцарь намерен спеть Алисе «очень, очень красивую песню»:

— Когда я её пою, все рыдают… или…

— Или что? — спросила Алиса, не понимая, почему Рыцарь вдруг остановился.

В другой популярной сказке народный лекарь Богомол заключает после осмотра Буратино:

— Одно из двух: или пациент жив, или он умер. Если он жив — он останется жив или не останется жив. Если он мёртв — его можно оживать или нельзя оживить.

Это напоминает ситуацию из старой песенки, в которой тоже используется идея исключительного третьего:

Жила одна старушка,

И, если не скончалась —

Закон исключённого третьего кажется самоочевидным. Тем не менее высказывались предложения отказаться от него или ограничить его действие применительно к определённым высказываниям.

В частности, Аристотель сомневался в приложимости этого закона к высказываниям о будущих событиях. В настоящий момент наступление некоторых из них ещё не предопределено. Нет причины ни для того, чтобы они произошли, ни для того, чтобы они не случились. «Через сто лет в этот же день будет идти дождь» — это высказывание сейчас, скорее всего, ни истинно, ни ложно. Таким же является его отрицание. Но закон исключённого третьего утверждает, что или само высказывание, или его отрицание истинно. Значит, заключает Аристотель, хотя и без особой уверенности, данный закон следует ограничить одними высказываниями о прошлом и настоящем и не прилагать его к высказываниям о будущем.

Немецкий философ Гегель весьма иронично отзывался как о законе противоречия, так и о законе исключённого третьего. Последний он представлял, в частности, в такой форме: дух является зелёным или не является зелёным, и задавал каверзный, как ему казалось, вопрос: какое из этих двух утверждений истинно?

Ответ на этот вопрос не представляет, однако, труда. Ни одно из двух утверждений: «Дух — зелёный» и «Дух — не зелёный» не является истинным, поскольку оба они бессмысленные. Закон исключённого третьего приложим только к осмысленным высказываниям. Только они могут быть истинными или ложными. Бессмысленное же не истинно и не ложно.

Резкой, но хорошо обоснованной критике подверг закон исключённого третьего голландский математик Л. Брауэр. В начале этого века он опубликовал три статьи, в которых выразил сомнение в неограниченной приложимости законов логики и прежде всего — закона исключённого третьего. Первая статья не превышала трех страниц, вторая — четырех, а вместе они не занимали и семнадцати страниц. Но впечатление, произведённое ими, было чрезвычайно сильным.

Брауэр был убеждён, что логические законы не являются абсолютными истинами, не зависящими от того, к чему они прилагаются. Возражая против закона исключённого третьего, он настаивал на том, что кроме утверждения и его отрицания имеется ещё третья возможность, которую нельзя исключить. Она обнаруживает себя при рассуждениях о бесконечных множествах объектов.

Допустим, что утверждается существование объекта с определённым свойством. Если множество, в которое входит этот объект, конечно, то можно перебрать все объекты. Это позволит выяснить, какое из следующих двух утверждений истинно: «В данном множестве есть объект с указанным свойством» или же «В этом множестве нет такого объекта». Закон исключённого третьего здесь справедлив.

Но когда множество бесконечно, объекты его невозможно перебрать. Если в процессе перебора будет найден объект с требуемым свойством, первое из указанных утверждений подтвердится. Но если найти этот объект не удастся, ни о первом, ни о втором из утверждений нельзя ничего сказать, поскольку перебор не проведён до конца. Закон исключённого третьего здесь не действует: ни утверждение о существовании объекта с заданным свойством, ни отрицание этого утверждения не является истинным.

Ограничение Брауэром сферы действия этого закона существенно сужало круг тех способов рассуждения, которые применимы в математике. Это сразу же вызвало резкую оппозицию многих математиков, особенно старшего поколения. «Изъять из математики принцип исключённого третьего, — заявлял немецкий математик Д. Гильберт, — все равно, что запретить боксёру пользоваться кулаками.

Критика Брауэром закона исключённого третьего привела к созданию нового направления в логике — так называемой интуиционистской логики. В последней не принимается данный закон и отбрасываются все те способы рассуждения, которые с ним связаны. Среди них — доказательства путём приведения к противоречию, или абсурду.

С законом исключённого третьего косвенно связан следующий методологический принцип: анализ каждого объекта должен вестись до тех пор и быть настолько полным, чтобы относительно любого утверждения об этом объекте можно было решить, истинно оно или нет. Это требование полноты и всесторонности исследования не относится, конечно, к законам логики. Оно полезно, но нередко оказывается невыполнимым. В случае рассуждений о бесконечных и неопределённых совокупностях объектов, об изменяющихся, текущих состояниях и т.п. изучение объекта не всегда способно достичь такой полноты, чтобы на любой вопрос о нем удалось ответить однозначно «да» или «нет».

Закон исключённого третьего

Закон исключённого третьего — это один из основных общелогических принципов, согласно которому в процессе рассуждения всякое суждение или истинно, или ложно. Данный закон устанавливает связь между противоречащими друг другу осмысленными высказываниями (в рассуждении, в тексте или теории): одно (и только одно) из них истинно, другое ложно. Относится к четырём так называемым основополагающим логическим законам — закону тождества, закону противоречия, закону исключённого третьего и закону достаточного основания (см. Законы логики), которые подразумевают наиболее общие принципы (или постулаты) теоретического мышления и используются при оперировании понятиями и суждениями, в умозаключениях, доказательствах и опровержениях, и поэтому присутствуют практически во всех логических системах.

Закон исключённого третьего подразумевает, что если истинно A, то не истинно — не-A, либо наоборот, неистинно A и истинно не-A. Здесь буква A обозначает произвольное высказывание. Символически закон выражается формулой:

Третьего не дано, как не дано ещё какого-либо B, которое претендовало бы на выражение истины. Таким образом, само название закона выражает его смысл: дело обстоит так, как говорится в рассматриваемом высказывании, или так, как говорится в его отрицании, и никакой третьей возможности нет.

Закон исключённого третьего непосредственно связан с законом противоречия (см. Закон противоречия), согласно которому два взаимно противоречащих высказывания не могут быть истинными в одно и то же время и в одном и том же отношении (то есть одно из них должно быть ложным). Оба эти закона были впервые сформулированы Аристотелем в его «Метафизике» (IV, 8); в применении к атрибутивным высказываниям вида «B есть C» они рассматривались также в его «Аналитиках». Впоследствии эти законы наряду с законом тождества («A есть A») были приняты схоластами в качестве основных законов логики. Оригинальная формулировка Аристотеля: «Оба утверждения A и не-A не могут быть одновременно ложны». Наряду с этим, в «Метафизике» встречается (не как закон, а как способ рассуждения) другая формулировка, в настоящее время более употребимая: «Одно из утверждений A или не-A должно быть истинным». Эта формулировка известна как сильный закон исключённого третьего и получила в схоластической логике название tertium non datur.

Аристотель указал также границы применимости tertium non datur, рассмотрев пример неопределённого высказывания: «Завтра будет морское сражение», которое сегодня не истинно и не ложно. Данный пример можно представить в следующем виде:

    Предположим, сегодня истинно, что завтра будет морское сражение. Из этого следует, что не может быть, чтобы завтра не было морского сражения. Следовательно, необходимо, чтобы завтра морское сражение произошло. Подобно этому тезису, если сегодня ложно, что завтра будет морское сражение, то необходимо, чтобы морское сражение завтра не произошло. Но высказывание о том, что завтра произойдёт морское сражение, сегодня истинно или ложно (логический принцип двузначности, в соответствии с которым всякое высказывание является либо истинным, либо ложным, то есть принимает одно из двух возможных истинностных значений — «истинно» и «ложно»). Принцип двузначности предлагает нам выбрать одну из этих двух альтернатив как верную, то есть или необходимо, чтобы морское сражение завтра произошло, или необходимо, чтобы оно завтра не произошло. В самом деле, если сегодня высказано «Завтра будет морское сражение или завтра не будет морского сражения», то это высказывание будет неопределённым, если неопределённы образующие его части. Но утверждение «Завтра будет морское сражение или неверно, что завтра будет морское сражение» будет истинно: если высказывание «Завтра будет морское сражение» неопределённо, то высказывание «Неверно, что завтра будет морское сражение» истинно.

Аристотель считал, что закон исключённого третьего следует ограничить высказываниями о прошлом и настоящем и не прилагать его к высказываниям о неопределённых будущих событиях, то есть к таким, наступление которых в настоящий момент ещё не предопределено, поскольку нет причины ни для того, чтобы они произошли, ни для того, чтобы они не случились.

От Аристотеля идёт традиция давать закону исключённого третьего три разные интерпретации:

  1. Логическая интерпретация. Закон понимается как принцип логики о высказываниях и их истинности: или высказывание, или его отрицание должно быть истинным.
  2. Онтологическая интерпретация. Закон понимается как утверждение об устройстве мира: всякий объект или реально существует, или не существует.
  3. Методологическая интерпретация. Закон понимается как принцип методологии научного познания: исследование каждого объекта должно вестись до тех пор и быть настолько полным, чтобы относительно каждого утверждения об этом объекте можно было решить, истинно оно или нет.

    Закон исключённого третьего содержит в себе следующие предписания:

  4. Устанавливается альтернативность A и не-A и предлагается сделать выбор между ними по истинностному признаку.
  5. Запрещается выбирать в качестве альтернативы ещё какие-либо суждения.
  6. Устанавливается отношение контрарности (противоположности) между альтернативами таким образом, что одна из них является отрицанием другой.
  7. Трактуется универсальный приём логического мышления, согласно которому противоположное истине есть ложь.

    На языке математической логики сильный закон исключённого третьего выражается формулой A ⋁ ¬A, которая часто подменяет его в современных математизированных работах и называется математическим законом исключённого третьего. Но последний не эквивалентен ни сильному закону исключённого третьего, ни аристотелеву закону. В частности, в алгебраической интерпретации со значениями в булевой алгебре выполнены все законы классической логики, но как A, так и ¬A могут быть неистинны. Сильный закон исключённого третьего математически означает полноту используемой теории, что практически недостижимо. Так, в случае рассуждений о бесконечных и неопределённых совокупностях объектов, об изменяющихся, текущих и тому подобных состояниях изучение объекта не всегда способно достичь такой полноты, чтобы на любой вопрос о нём удалось ответить однозначно «да» или «нет».

    Сильный закон исключённого третьего оказался тем критическими местом, вокруг которого развивались дискуссии в течение всего времени существования логики как науки. Стоики и эпикурейцы рассматривали логики, несовместимые с законом исключённого третьего (как правило, не замечая разницы между его сильной и формулировкой Аристотеля). Интуиционизм начинался с утверждения о недостоверности сильного закона исключённого третьего, но он опровергает его достаточно тонко, сохраняя слабый закон исключённого третьего и придавая ему точную математическую формулировку: ¬¬ (A ⋁ ¬A), не вводя дополнительных логических значений. Эту формулировку ввёл Л. Брауэр в рамках критики применимости законов классической логики в математике (1908). Впоследствии её назвали брауэровым законом исключённого третьего. Брауэр был убеждён, что логические законы не являются абсолютными истинами, не зависящими от того, к чему они прилагаются. Возражая против закона исключённого третьего, он настаивал на том, что кроме утверждения и его отрицания имеется ещё третья возможность, которую нельзя исключить: она обнаруживает себя при рассуждениях о бесконечных множествах объектов. Ограничение Брауэром сферы действия этого закона существенно сужало круг тех способов рассуждения, которые применимы в математике и это сразу же вызвало резкую оппозицию многих математиков. Первое формальное доказательство брауэрова закона дал В. И. Гливенко (1928). Критика Брауэром закона исключённого третьего положила начало новому направлению в формальной логике (см. Логика формальная) — интуиционистской логике. В ней не принимается данный закон и отбрасываются все те способы рассуждения, которые с ним связаны.

    В целом, закон исключённого третьего представляется теперь спорным законом логики, более того, в некоторых рассуждениях его следует считать ложным. Общая критика закона (в его сильной форме) сводится к следующим положениям. Он применим для рассмотрения терминов в фиксированной обстановке с фиксированной точки зрения. Он не подходит для меняющейся обстановки и субъективных понятий. Он не допустим даже для терминов, если исследователя интересует не просто доказательство, а построение. Тем не менее, во всех указанных случаях иногда его использование корректно и весьма эффективно, но требует дополнительных обоснований.

    gtmarket.ru

    Закон исключённого третьего — закон классической логики, состоящий в том, что из двух высказываний — «А» или «не А» — одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно ложными, одно из них необходимо истинно. Закон исключённого третьего является одним из основополагающих принципов современной математики.

    Содержание

    В математической логике закон исключенного третьего выражается формулой

    где 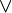— знак дизъюнкции, — знак отрицания.

    Гораздо более тонкий пример применения закона исключённого третьего, который хорошо демонстрирует, почему он не является приемлемым с точки зрения интуиционизма, состоит в следующем. Предположим, что мы хотим доказать теорему, что существуют два таких иррациональных числа a и b, что a b рационально. Известно, что 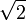иррационально. Рассмотрим 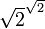. Если данное число рационально, то теорема доказана. Иначе возьмём 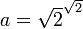и 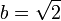. Тогда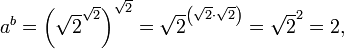

    то есть рациональное число. По закону исключённого третьего иных вариантов быть не может. Поэтому, теорема в общем случае доказана. Причём доказательство предельно просто и элементарно. С другой стороны, если принять интуиционистскую точку зрения и отказаться от закона исключённого третьего, теорема хотя и может быть доказана, но доказательство её становится исключительно сложным.

      Wikimedia Foundation . 2010 .

      ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО — один из основных законов классической двузначной логики, исходившей из наличия у суждений только двух истинностных значений: истины или лжи. Его формальная запись такова: А V А (где V означает исключающую дизъюнкцию: либо либо). Согласно этому… … Философия науки: Словарь основных терминов

      Закон исключения третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

      ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН — один из важнейших законов формальной логики, состоящий в том, что для всякого высказывания А истинно по крайней мере одно из двух: само А или его отрицание. Был известен уже Аристотелю. См. Принцип исключенного третьего. Философская Энциклопедия … Философская энциклопедия

      исключенного третьего закон — ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН один из трех главных законов логики, сформулированных Аристотелем. Его оригинальная формулировка гласит: «Оба утверждения А и не А не могут быть одновременно ложны». В «Метафизике» Аристотеля… … Энциклопедия эпистемологии и философии науки

      ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН — закон классической логики, состоящий в том, что одно из двух высказываний Л и не Л является истинным. В математической логике И. т. з. выражается формулой где знак дизъюнкции, знак отрицания. С интуиционистской (конструктивной) точки зрения… … Математическая энциклопедия

      Принцип исключенного третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

      ПРИНЦИП ИСКЛЮЧЕННОГО ТРЕТЬЕГО — (распространенное лат. название – tertium non datur) – логич. закон, состоящий в том, что для всякого высказывания Л истинно по крайней мере одно из двух высказываний: само А или его отрицание (символически пишется A∨A и читается: А или не A).… … Философская энциклопедия

      ЗАКОН ЛОГИЧЕСКИЙ — ЗАКОН ЛОГИЧЕСКИЙ общее название законов, образующих основу логической дедукции. Понятие о законах логики восходит к древнегреческому понятию о logos e как предпосылке объективной (“природной”) правильности рассуждений. Собственно логическое… … Философская энциклопедия

      dic.academic.ru

      Закон исключенного третьего

      С интуиционистской (и, в частности, конструктивистской) точки зрения, установление истинности высказывания вида «А или не А» означает установление истинности A или истинности его отрицания, 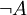. Поскольку не существует общего метода, позволяющего для каждого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключенного третьего подвергается критике со стороны представителей интуиционистского и конструктивного направлений в основаниях математики.

      Формулировка

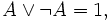
      Другие формулировки

      Подобный смысл имеют другие логические законы, многие из которых сложились исторически.

      Предположим, что P представляет собой утверждение «Сократ смертен». Тогда закон исключённого третьего для P примет вид: «Сократ смертен или Сократ бессмертен», откуда ясно, что закон отсекает все иные варианты, при которых Сократ и не смертен и не бессмертен. Последнее — это и есть то самое «третье», которое исключается. Этим также обусловлено латинское название данного закона: «лат. tertium non datur », то есть «третьего не дано».

      Примечания

    1. ↑ Zena M. Ariola and Hugo Herbelin. Minimal classical logic and control operators. In Thirtieth International Colloquium on Automata, Languages and Programming , ICALP’03, Eindhoven, The Netherlands, June 30 — July 4, 2003, volume 2719 of Lecture Notes in Computer Science, pages 871—885. Springer-Verlag, 2003.[1]

      Смотри также

      Смотреть что такое «Закон исключенного третьего» в других словарях:

      закон исключенного третьего — логический закон, согласно которому истинно или само высказывание, или его отрицание. Закон устанавливает связь между противоречащими друг другу высказываниями: одно из таких высказываний истинно. Напр.: Аристотель умер в 322 г. до н. э. или он… … Словарь терминов логики

      исключенного третьего закон — см.: Закон исключенного третьего … Словарь терминов логики