Задачи для решения по теме газовые законы

Примеры решения задач по теме «Газовые законы»

«Физика — 10 класс»

Если при переходе газа из начального состояния в конечное один из параметров не меняется, то разумно использовать один из газовых законов (10.6), (10.7) или (10.9).

Баллон вместимостью V1 = 0,02 м3, содержащий воздух под давлением Pi — 4 • 10° Па, соединяют с баллоном вместимостью V2 = 0,06 м3, из которого воздух выкачан.
Определите давление р, которое установится в сосудах.
Температура постоянна.

Воздух из первого баллона займёт весь предоставленный ему объём V1 + V2.
По закону Бойля—Мариотта p1V1 = p(V2 + V1).

Отсюда искомое давление

В запаянной пробирке находится воздух при атмосферном давлении и температуре 300 К.
При нагревании пробирки на 100 °С она лопнула.
Определите, какое максимальное давление выдерживает пробирка.

Объём воздуха при нагревании остаётся постоянным.

Для определения давления в пробирке при нагревании до 100 °С применяем закон Шарля

По условию Т2 = 400 К.
Заметим, что изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия.

Однако разорваться пробирке мешает атмосферное давление.
Тогда окончательно давление, которое может выдержать пробирка, рmах = ратм + р2 ≈ 2,25 атм.

При нагревании газа при постоянном объёме на 1 К давление увеличилось на 0,2 %.
Чему равна начальная температура газа?

Газ нагревается при постоянном объёме — процесс изохорный.
По закону Шарля

где Т2 = Т1 + ΔТ.
Из условия задачи следует, что р2 = p1 • 1,002, т. е.

откуда Т1 = ΔТ/0,002 = 500 К.

Давление воздуха внутри бутылки, закрытой пробкой, равно 0,1 МПа при температуре t1 = 7 °С.
На сколько градусов нужно нагреть воздух в бутылке, чтобы пробка вылетела?
Без нагревания пробку можно вынуть, прикладывая к ней силу 30 Н.
Площадь поперечного сечения пробки 2 см 2 .

Чтобы пробка вылетела из бутылки, необходимо, чтобы давление воздуха в бутылке было равно

При нагревании объём не изменяется.
По закону Шарля

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Устали? — Отдыхаем!

  • Парадоксы
  • Это интересно
  • История техники
  • Физика детям
  • Библиотека
  • Знаете ли вы
  • История физики
  • Любознательным
  • Мысли вслух
  • Выпускникам
    Как сдавать экзамены?
    Тактика тестирования
    Знаешь ли ты себя?
    На урок
  • Поделиться

class-fizika.ru

Примеры решения задач к главе «Уравнение состояния идеального газа. Газовые законы»

В задачах на использование газовых законов встречаются обычно следующие ситуации:

а) известны макроскопические параметры в начальном состоянии газа и некоторые параметры в конечном состоянии.

Если при переходе из начального состояния в конечное один из параметров не меняется, то при изотермическом процессе можно пользоваться законом Бойля-Мариотта в форме (3.6) или в эквивалентной форме 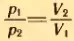, следующей из (З.6). При изобарном процессе нужно пользоваться законом Гей-Люссака (3.8) или (3.7); при изохорном – законом Шарля (3.10) или (3.9).

Если меняются все три параметра, то надо использовать уравнение состояния (3.4) или (3.5);

б) известна часть макроскопических параметров в определенном состоянии газа. Надо найти неизвестные величины. В этих случаях удобнее всего пользоваться уравнением Менделеева-Клапейрона (3.4);

в) во многих задачах требуется построение графиков, изображавших разного рода процессы. Для построения графиков нужно знать зависимость параметров друг от друга. Эта зависимость в общем случае дается уравнением состояния, а в частных случаях – газовыми законами.

При решении всех задач надо четко представлять себе, каково начальное состояние системы и какого рода процесс переводит ее в конечное состояние.

1. Баллон вместимостью V1 = 0,02 м 3 , содержавший воздух под давлением p1 = 4 * 10 5 Па, соединяют с баллоном вместимостью V2 = 0,06 м 3 , из которого воздух выкачан. Найти давление p , установившееся в сосудах. Температура постоянна.

Решение . Воздух из первого баллона займет весь предоставленный ему объем V1 + V2. По закону Бойля-Мариотта

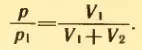
Отсюда искомое давление равно:

2. На какую долю первоначального объема увеличится объем газа, находящегося при температуре t = 27°C, если нагреть его на 1°C при постоянном давлении?

Решение . Пусть V1 и T1 = 273 К + t = 300 К – первоначальные значения параметров состояния газа, V2 и T2 = T1 + 1 К – конечные значения тех же параметров.

По закону Гей-Люссака

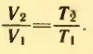
Равенство не изменится, если из левой и правой частей вычесть по единице:

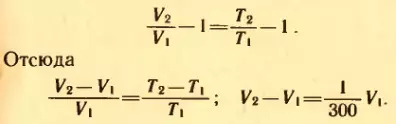
Объем газа увеличится на 1/300 долю первоначального.

3. Плотность воздуха при нормальных условиях (т. е. при t0 = 0°C и нормальном атмосферном давлении p0 = 101325 Па) ρ = 1,29 кг/м 3 . Найти среднюю молярную массу M воздуха.

Решение . Уравнение состояния идеального газа при нормальных условиях имеет вид:
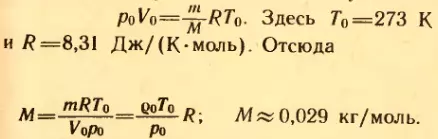
4. Построить изобары для 2 г водорода при нормальном атмосферном давлении p0 в осях p, T; p, V; V, T.

Решение . На графиках зависимости p от T и p от V изобара будет представлять собой прямую, параллельную либо оси T, либо оси V (рис. 37, а и б).

phscs.ru

§ 66. Примеры решения задач по теме «Газовые законы»

Для этого нужно знать зависимость параметров друг от друга, которая в общем случае даётся уравнением состояния, а в частных — газовыми законами.

Задача 1. Баллон вместимостью V1 = 0,02 м3, содержащий воздух под давлением Pi — 4 • 10° Па, соединяют с баллоном вместимостью V2 = 0,06 м3, из которого воздух выкачан. Определите давление р, которое установится в сосудах. Температура постоянна.

Р е ш е н и е. Воздух из первого баллона займёт весь предоставленный ему объём V1 + V2. По закону Бойля—Мариотта p1V1 = p(V2 + V1).

Отсюда искомое давление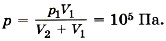

Задача 2. В запаянной пробирке находится воздух при атмосферном давлении и температуре 300 К. При нагревании пробирки на 100 °С она лопнула. Определите, какое максимальное давление выдерживает пробирка.

Р е ш е н и е. Объём воздуха при нагревании остаётся постоянным.

Для определения давления в пробирке при нагревании до 100 °С применяем закон Шарля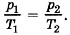

По условию Т2 = 400 К. Заметим, что изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия.

Тогда давление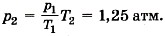

Однако разорваться пробирке мешает атмосферное давление. Тогда окончательно давление, которое может выдержать пробирка, рmах = ратм + р2 ≈ 2,25 атм.

Задача 3. При нагревании газа при постоянном объёме на 1 К давление увеличилось на 0,2 %. Чему равна начальная температура газа?

Р е ш е н и е. Газ нагревается при постоянном объёме — процесс изохорный. По закону Шарля 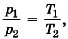где Т2 = Т1 + ΔТ. Из условия задачи следует, что р2 = p1 • 1,002, т. е. 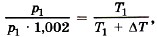откуда Т1 = ΔТ/0,002 = 500 К.

Задача 4. Давление воздуха внутри бутылки, закрытой пробкой, равно 0,1 МПа при температуре t1 = 7 °С. На сколько градусов нужно нагреть воздух в бутылке, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 30 Н. Площадь поперечного сечения пробки 2 см 2 .

Р е ш е н и е. Чтобы пробка вылетела из бутылки, необходимо, чтобы давление воздуха в бутылке было равно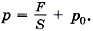

При нагревании объём не изменяется. По закону Шарля 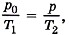откуда 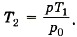Следовательно,

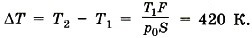
Задачи для самостоятельного решения

1. Компрессор, обеспечивающий работу отбойных молотков, засасывает из атмосферы воздух объёмом V = 100 л в 1 с. Сколько отбойных молотков может работать от этого компрессора, если для каждого молотка необходимо обеспечить подачу воздуха объёмом V1 = 100 см 3 в 1 с при давлении р = 5 МПа? Атмосферное давление р0 = 100 кПа.

2. Определите температуру газа, находящегося в закрытом сосуде, если давление газа увеличивается на 0,4 % от первоначального давления при нагревании на 1 К.

3. Высота пика Ленина на Памире равна 7134 м. Атмосферное давление на этой высоте равно 3,8 • 10 4 Па. Определите плотность воздуха на вершине пика при температуре 0 °С, если плотность воздуха при нормальных условиях 1,29 кг/м 3 .

Образцы заданий ЕГЭ

С1. Идеальный газ изотермически сжали из состояния с объёмом 6 л так, что давление газа изменилось в 3 раза. На сколько уменьшился объём газа в этом процессе?

С2. Поршень площадью 10 см 2 и массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом его герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с 2 ? Изменение температуры газа не учитывайте.

С3. С идеальным газом происходит изобарный процесс, в котором для увеличения объёма газа на 150 дм 3 его температуру увеличивают в 2 раза. Масса газа постоянна. Каким был первоначальный объём газа?

С4. Идеальный одноатомный газ в количестве ν = 0,09 моль находится в равновесии в вертикальном цилиндре под поршнем массой 5 кг. Трение между поршнем и стенками цилиндра отсутствует. Внешнее атмосферное давление p0 = 100 кПа. В результате нагревания газа поршень поднялся на высоту Δh = 4 см, а температура газа повысилась на ΔТ = 16 К. Чему равна площадь поршня?

С5. Идеальный газ изохорно нагревают так, что его температура изменяется на ΔТ = 240 К, а давление — в 1,8 раза. Масса газа постоянна. Определите начальную температуру газа по шкале Кельвина.

www.xn--24-6kct3an.xn--p1ai

Газовые законы. Решение задач

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Методическая разработка урока по физике в 10 классе по теме: «Газовые законы. Решение задач на изопроцессы»

Продолжительность урока – 90 минут(2- урока)

— уметь выводить газовые законы, понимать, читать и строить графики изопроцессов;

— способствовать выработке умений применять полученные знания при работе с графиками;

— формировать умение применять полученные знания на практике;

— развивать аналитические и практические умения учащихся;

— развивать навыки самостоятельной и исследовательской работы, анализа своей работы, взаимоконтроля, развивать устную речь, с целью развития познавательного интереса учащихся;

— воспитывать умение высказывать свою точку зрения, слушать других, принимать участие в диалоге;

— формировать способности к позитивному сотрудничеству;

— формирование мировоззренческих понятий о познаваемости мира, для воспитания чувства само- и взаимоуважения при работе в парах, группах.

Тип урока: урок изучения и первичного закрепления новых знаний.

Формы организации познавательной деятельности:

Техническое обеспечение урока : мультимедийный проектор, компьютер, интерактивная доска, презентация «Газовые законы», карточки-задания, листы самооценки.

2. Проверка домашнего задания (20 мин)

— Какова тема прошлого урока?

— Как выглядит уравнение Менделеева – Клапейрона?

— Для чего нужно это уравнение состояния для идеального газа?

Для проверки усвоения навыков решения задач на уравнение состояния идеального газа выполним самостоятельную работу. На столах лежат карточки – задания. Работаем с карточкой номер 1 по вариантам. Ваша задача – заполнить таблицу (приложение 1).

2 человека по вариантам выполняют тоже задание на полузакрытых досках. (слайд 1)

Учитель : Для проверки работы нам нужны критерии ее оценивания, давайте вместе сформулируем критерии – за что можно поставить оценку (учащиеся предлагают свои критерии).

На обратной стороне карточки записаны критерии оценивания работы. Посмотрите внимательно – совпадают ли наши критерии с теми, что предложены на листах? Обменяйтесь работами.

Проверяем задания, выполненные на доске, и сверяем их с ответами в ваших карточках. Ученики, работающие у доски, вносят свои ответы в таблицу на интерактивной доске.

Методом взаимоконтроля проверьте правильность выполнения задания и выставьте оценку. Передаем карточку с последних парт на первые.

Уравнение состояния идеального газа или связывает 3 макроскопических параметра, каких? (слайд 2)

Количественная зависимость между двумя параметрами газа при фиксированном значении третьего называют газовыми законами .

— Как вы считаете, сколько их и какие это могут быть уравнения – законы?

— Озвучьте тему нашего урока (слайд 3) и сформулируйте его цель ( спросить несколько человек и обобщить цель урока).

4. Изучение нового материала (15 мин.):

Учитель : Процессы, протекающие при неизменном значении одного из параметров называют изопроцессами (от греческого слова «изос» — равный). Изопроцесс – это идеализированная модель реального процесса, которая только приближенно отражает действительность.

— Сколько параметров связывает между собой уравнение состояния?

— Сколько изопроцессов мы должны изучить?

Для групповой работы класс делится на три группы (три ряда). Работая с учебником ( § 69 на стр. 186), каждая группа изучает изопроцесс по следующему плану исследования: (слайд 4)

1) определение изопроцесса;

2) формула закона, название закона;

3) историческая справка;

4) графическое изображение процесса;

5) название графика.

Итак, рассмотрим с вами три изопроцесса. Каких?

Каждая группа у доски представляет свой закон согласно плану. Одна группа выступает, другие две группы записывают в тетрадь.

Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим («изос» — равный; «термос» — теплый)

Историческая справка: этот закон экспериментально был открыт в 1662 г английским ученым Р.Бойлем и независимо от него несколько позже в 1676 г французским физиком Э.Мариоттом.

Поэтому оно носит название закона Бойля – Мариотта.

Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой .

Учитель: Этот изотермический процесс можно изобразить и в других координатных осях. Изобразим изотерму в координатах рТ и V Т.

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (греч. сл. «барос» — тяжелый, вес)

Историческая справка: этот закон был установлен экспериментально в 1802 г. французским физиком Ж. Гей-Люссаком и носит название закона Гей-Люссака.

Графическая зависимость объема от температуры изображается прямой линией – изобарой . При очень низких температурах закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

Учитель: Изобразим изобару в координатах рТ и рТ.

3 группа. III . Изохорный процесс (слайд 7)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (греч. сл. «хорема» — вместимость).

Историческая справка: этот газовый закон был установлен в 1787 г французским физиком Ж. Шарлем и носит название закона Шарля .

Графическая зависимость давления от температуры изображается прямой линией – изохорой .

Учитель: Изобразим изохору в координатах V Т и р V .

5. Закрепление пройденной темы ( 40 мин)

Учитель: Для проверки усвоения этого теоретического материала, я предлагаю провести небольшой проверочный тест. Можно воспользоваться своими конспектами. (тест выводится на экран, с последующей проверкой)

1. Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон …

2. Какой из приведенных ниже графиков соответствует изобарному расширению? ( А )

3. Какие три процесса представлены на диаграммах рисунка?

А. изохорный, изотермический, изобарный

В. изобарный, изохорный, изотермический

С. изохорный, изобарный, изотермический

Учитель : Итак, мы с вами изучили газовые законы. Какие это законы? А какова цель нашего урока? (спросить 2-3 чел.)

Наша задача – научиться представлять изопроцессы в различных координатах. Например, такой процесс:

Учитель: Рассмотрим способы решения задач на построение графиков изопроцессов в осях р V , р T , VT , если представлен один из графиков.

Важно запомнить , что для постоянной массы газа:

Температура выше на той изотерме, график которой лежит выше в координатах р V

Давление больше на той изобаре, график которой лежит ниже в координатах VT

Объем больше на той изохоре, график которой лежит ниже в координатах рТ

Вывод : для выяснения характера изменения параметра необходимо проводить соответствующие ему графики изопроцессов (изотермы, изобары, изохоры)

Задание 1. Увеличивается или уменьшается давление газа в ходе процесса 1-2? ( слайд 10)

Проведем изобары через точки 1 и 2.

В ходе процесса осуществляется переход с изобары, лежащей выше, на изобару, лежащую ниже, следовательно, давление газа в ходе процесса 1 – 2 увеличивается.

Задание 2 . Представьте процесс в координатах pT , VT . (слайд 11)

1) записываем уравнение состояния газа

Начинаем построение точки таким образом, чтобы от нее можно было «идти» свободно в любом направлении. Смотрим подсказки ( в анализе ).

Учитель : На столах у вас лежит карточка номер 2 . Каждому варианту предлагается самостоятельно решить задачу на построение графиков изопроцессов. Можно воспользоваться вашими конспектами. (приложение 2)

Учитель : Время на выполнение работы закончено. Подпишите свои работы.

6. Подведение итогов. Рефлексия. (7 мин)

Учитель : Подведем итоги нашего урока (блиц-опрос).

— Какова тема сегодняшнего занятия?

— Вы все успешно справились с поставленной целью? Какой?

— Что вызвало у вас затруднение? Что не получилось?

А сейчас каждый из вас оценит свою деятельность на протяжении всего нашего занятия. На обратной стороне вашей карты № 2 изображена карта самооценки, на которой вы должны сделать пометки напротив каждого этапа, затем по ним вычертить график.

Ваши карты-задания сдайте на проверку, каждому будут выставлены оценки и озвучены на следующем уроке.

Наше занятие закончилось. Ваше домашнее задание будет следующим:

§ 69, сборник задач Рымкевича № 544. Для желающих: с помощью диаграмм изобразить какую-нибудь фигуру. (слайд 12)

Спасибо за работу и всех благодарю за сотрудничество. До свидания.

Список использованной литературы:

Физика. 10 класс: учеб.для общеобразват. учреждений: базовый и профил. уровни / Г.Я. мякишев, Б.Б. Буховцев, Н.Н. Сотский; под ред. В.И. Николаева, Н.А. Парфентьевой. – 20-е изд. – М.: Просвещение, 2011.

Физика. 10 класс. Тесты: в 2 ч. / Ю.Н. Сычев. Саратов: Лицей, 2012.

Физика. 10 класс. Поурочные планы. / сост. Г.В. Маркина. – издательство «Учитель», Волгоград, 2000 (стр. 21)

Универсальные поурочные разработки по физике: 10 класс. / В.А. Волков. – М.: ВАКО, 2007 (стр. 217)

Задачи по физике для профильной школы с примерами решений. 10-11 классы. / Л.А. Кирик, Л.Э. Генденштейн, И.М. Гельфгат; под ред. В.А. Орлова. – М.: ИЛЕКСА, 2008 (задача № 17.39 стр. 130, 134)

1. Запишите формулу Менделеева – Клапейрона

2. Запишите формулу для вычисления массы газа m :…………..…….

3. Запишите формулу для вычисления объема газа V :……………….

infourok.ru

Методическая разработка по физике (10 класс) по теме:
Разработка урока: Решение задач по теме «Газовые законы»

В разработке урока присутствует повторение темы «Газовые законы». Рассматривается решение качественных и экспериментальных задач. экспериментальные задачи сопровождаются проведением простых опытов с использованием воздушных шаров. Рассматривается задача на условие подъёма тел в воздухе. Наиболее интересный момент урока: сначала ученики теоретически рассчитывают: «Сколько надо гелиевых шариков, чтобы шоколадка поднялась в воздух?», а затем им предоставляется возможность практически это проверить. Это активизирует учащихся и создаёт на уроке положительный эмоциональный фон.

Предварительный просмотр:

Решение задач по теме «Газовые законы».

Образовательная: закрепить знания по теме «Газовые законы», способствовать умению обучающихся использовать физические законы для решения прикладных задач, связанных с повседневной жизнью, продолжить формирование умения применять знания физики для объяснения наблюдаемых явлений и опытов.

Воспитательная: способствовать формированию интереса к физике, воспитывать чувства само- и взаимоответственности, уверенности в себе.

Развивающая: способствовать развитию самостоятельной познавательной активности обучающихся, развивать память, логическое мышление.

Методическая: показать эффективность использования нетрадиционных методов ведения урока, способствующих активизации познавательной деятельности обучающихся.

Тип урока: урок закрепления знаний

Методы обучения: репродуктивный, частично-поисковый, исследовательский

Формы проведения урока: групповая, индивидуальная

Межпредметные связи: биология: «Органы дыхания человека», математика «Объём шара».

КМО: компьютер, мультимедиапроектор, карточки с формулами и их названиями, пластиковая бутылка, дно которой отрезано и затянуто резиновой плёнкой, три воздушных шарика – пустой, надутый и наполненный водой, трёхлитровая банка, чайник с кипятком, гелиевые шарики, шоколадка, термометр, справочник, измерительная лента, пластиковая бутылка с небольшим отверстием.

  • Организационный момент
  • Приветствие учащихся
  • Проверка готовности учащихся к уроку
  • Сообщение темы и цели урока
  1. Актуализация знаний
  2. Повторение физических величин (с помощью мультимедиапроектора).
  3. Повторение названия изопроцессов и газовых законов (с помощью мультимедиапроектора).
  4. Повторение основных формул. (Раздаются карточки с формулами.

    На доске – названия формул. Обучающиеся должны прикрепить формулу к её названию).

  5. Решение задач
  6. Устная разминка ( Обучающиеся отвечают на предложенные вопросы):
  7. Почему мыльные пузыри, наполненные воздухом, некоторое время поднимаются, а потом опускаются?
  8. Космический корабль, стартовав с Земли, вышел на околоземную орбиту. Как изменилось давление воздуха в герметично закрытом отсеке? Температура в отсеке не изменилась.
  9. Почему от горящих поленьев с треском отскакивают искры?
  10. При изготовлении ламп накаливания их баллоны заполняют азотом под давлением, значительно меньшим атмосферного. Почему это давление не делают равным атмосферному?
  11. Почему баллон с любым сжатым газом представляет большую опасность при пожаре?
  12. Когда до большего давления накачивают шины автомобилей: зимой или летом?
  13. Приведите примеры применения сжатого воздуха на шахте.
    1. Работа в тетрадях
    2. Из уравнения Менделеева – Клапейрона выведите формулу для вычисления плотности газов. От чего зависит плотность газа?
    3. Во сколько раз плотность углекислого газа отличается от плотности азота, если газы находятся при одинаковых условиях?
  14. Экспериментальные задачи

    1) Демонстрация «Модель лёгких». (Для этого используется пластиковая бутылка, дно которой отрезано и затянуто резиновой плёнкой. В бутылку вставлен воздушный шарик).

    Вопрос: Какой физиологический процесс здесь моделируется? Какой газовый закон здесь можно приближённо применить?

    2) Демонстрация «Шар в банке». (Для этого используется воздушный шарик, наполненный водой, трёхлитровая банка, чайник. После того, как банка прогрета горячей водой, на неё кладётся шарик. Постепенно он втягивается в банку.

    Вопрос: Почему так происходит? Какой изопроцесс здесь моделируется?

  15. На экране слайд «Праздник»

    Давайте создадим на уроке праздничную атмосферу. Украсим наш праздник воздушными шарами.

    Перед вами два шарика – воздушный и гелиевый. Отпустим их.

    Вопрос: Почему гелиевый шарик летит вверх, а воздушный – вниз?

    Какой же праздник без угощения? Пусть угощением у нас будет шоколадка.

    Добавим в наш праздник оригинальности. Заставим нашу шоколадку парить в воздухе.

    Вопрос: Как это сделать?

    Попробуем привязать к шоколадке гелиевый шарик. Ничего не выходит.

    Давайте попробуем с вами рассчитать, какое минимальное количество гелиевых шариков надо привязать к шоколадке, чтобы она не падала, а висела в воздухе?

    Сделать это непросто, но вполне возможно. Итак, начнём.

  16. Сделаем рисунок. Расставим силы, действующие на шарик и шоколадку. Для упрощения задачи будем рассматривать шарики и шоколадку как одно целое.

    Вопрос: Какая сила будет поднимать шоколадку? (Сила Архимеда)

  17. Вспомним закон Архимеда.
  18. Сформулируем и запишем условие подъёма шоколадки. (Силой сопротивления воздуха пренебрегаем).

    F A ≥ Mg + Nmg, где М – масса шоколадки, а m – масса шарика.

  19. Выведем формулу для расчёта необходимого количества гелиевых шариков.

    F A = ρ в VNg, где ρ в – плотность окружающего воздуха, V – объём шарика,

    N – количество шариков.

    ρ в VN = M + Nm; ρ в VN – Nm = M; N(ρ в V – m) = M; ρ в V = m в

    Масса шарика m складывается из массы его оболочки и массы гелия в нём.

    Из уравнения Менделеева – Клапейрона можно найти массы газов:

    Объём шара можно найти по формуле: V = π .

    Получаем конечную формулу:

    N = . Проверяем размерность.

    Для расчета в формулу надо поставить численные значения.

  20. Группы обучающихся получают задания:
  21. Определить массу шоколадки и оболочки шарика (М и m об ) в лаборатории продавцов (формула позволяет измерять массу в граммах).
  22. Измерить температуру окружающего воздуха и перевести её в кельвины (Т).
  23. Определить атмосферное давление (или перед занятиями или при помощи интернета). Перевести значение в паскали (р в ).
  24. Определить давление гелия в шарике (самое слабое место в расчётах – приходится доверяться сведениям из интернета). Перевести значение в паскали (р г ).
  25. По таблице Менделеева определить молярную массу гелия (М г в г/моль).
  26. В справочнике определить молярную массу воздуха (М в в г/моль).
  27. С помощью сантиметра измерить радиус шарика(R ш ).
  28. Записать значения постоянных и R.

    Полученные значения заносятся в таблицу и обучающиеся производят расчёт. Полученные результаты сравниваются и обсуждаются.

    Самому активному ученику предоставляется экспериментально проверить полученный результат. (На уроке брали «Милки Увэй». По расчётам выходит три шарика. Но если привязать три шарика, то шоколадка ёрзает на столе, но не поднимается. Обращаем внимание на знак≥ в условие подъёма. Привязываем 4 шарика – шоколадка поднимается к потолку.)

    Демонстрируется фрагмент из фильма «Три толстяка»

    Задание: Рассчитайте, сколько понадобится шаров, чтобы поднять человека массой 70 кг. Температура воздуха 25ºС. Радиус шара определяем визуально. Шары заполнены водородом. Атмосферное давление 760 мм рт.ст. Давление в шарике 780 мм рт.ст. (По кадру из фильма приблизительно оцениваем количество шаров, чтобы сравнить с результатом расчётов).

  29. Подведение итогов урока

    Обсуждаем, чему научились на уроке. Оцениваем работу обучающихся.

    nsportal.ru