Правило Лопиталя

Введите функцию и точку для предела, которому надо применить правило Лопиталя

Вычислим предел функции с помощью правила Лопиталя. Вы введёте функцию, для которой требуется вычислить предел и точку в которой предел должен сходиться.

• 
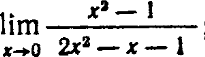
  • 0
  • (x^2-1)/(2*x^2-x-1)
• 
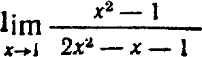
  • 1
  • 
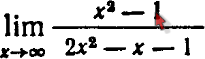
    • +oo
    • 
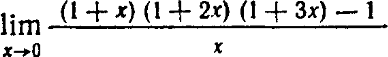
      • ((1+x)*(1+2*x)*(1+3*x)-1)/x
      • 
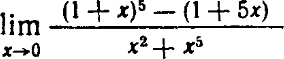
        • ((1+x)^5-(1+5*x))/(x^2+x^5)
        • 
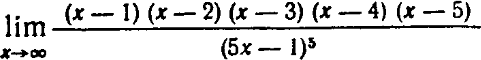
          • (x-1)*(x-2)*(x-3)*(x-4)*(x-5)/(5*x-1)^5
          • 
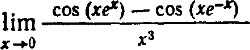
            • ( cos(x*e^x) — cos(x*e^(-x)) )/x^3
            • 
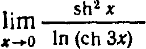
              • ( sinh(x) )^2 / ln( cosh(3*x) )

              Правила ввода выражений и функций

              Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

              absolute(x) Абсолютное значение x
              (модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x e e число, которое примерно равно 2.7 exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
              (Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) pi Число — «Пи», которое примерно равно 3.14 sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) sign(x) Функция — Знак x erf(x) Функция ошибок (Лапласа или интеграл вероятности)

              В выражениях можно применять следующие операции:

              Действительные числа вводить в виде 7.5, не 7,5 2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание

              www.kontrolnaya-rabota.ru

              Правило Лопиталя для чайников: определение, примеры решения, формулы

              Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.

              Правило Лопиталя: история и определение

              На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.

              Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.

              Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:

              Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

              Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:

              Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.

              Раскрытие неопределенностей по правилу Лопиталя

              В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:

              Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:

              Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:

              Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:

              Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.

              Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:

              Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.

              zen.yandex.ru

              Правило Лопиталя: теория и примеры решений

              Правило Лопиталя и раскрытие неопределённостей

              Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).

              Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

              Перейдём к формулировкам правил Лопиталя.

              Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю

              (),

              Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности

              (),

              то предел отношения этих функций равен пределу отношения их производных

              ().

              Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

              Замечания.

              1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.

              2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

              3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).

              К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

              Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»

              Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

              

              Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

              

              В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.

              Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

              .

              Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

              

              Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

              .

              

              Пример 4. Вычислить

              .

              Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

              

              Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

              Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

              .

              

              Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.

              Пример 6. Вычислить

              .

              

              Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.

              Пример 7. Вычислить

              .

              

              Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.

              Пример 8. Вычислить

              .

              

              Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.

              Применить правило Лопиталя самостоятельно, а затем посмотреть решение

              Пример 9. Вычислить

              .

              Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.

              Пример 10. Вычислить

              .

              Подсказка. Здесь правило Лопиталя придётся применять трижды.

              Раскрытие неопределённостей вида «ноль умножить на бесконечность»

              Пример 11. Вычислить

              .

              

              (здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как

              

              а затем применили правила Лопиталя).

              Пример 12. Вычислить

              .

              

              В этом примере использовано тригонометрическое тождество .

              Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»

              Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

              Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

              Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

              

              Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

              Пример 13. Вычислить, пользуясь правилом Лопиталя

              .

              

              Вычисляем предел выражения в показателе степени

              .

              .

              Пример 14. Вычислить, пользуясь правилом Лопиталя

              .

              

              .

              .

              Пример 15. Вычислить, пользуясь правилом Лопиталя

              .

              

              

              .

              Раскрытие неопределённостей вида «бесконечность минус бесконечность»

              Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: .

              Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:

              

              В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.

              Пример 16. Вычислить, пользуясь правилом Лопиталя

              .

              Решение. Пользуясь вышеперечисленными рекомендациями, получаем

              

              Пример 17. Вычислить, пользуясь правилом Лопиталя

              .

              function-x.ru

              

              Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.

              Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.

              Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

              

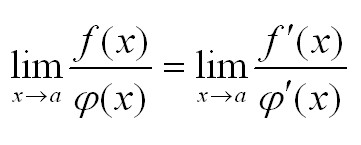
              Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

              В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:

              

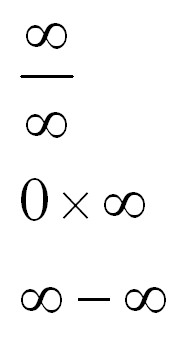
              Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.

              

              Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:

              

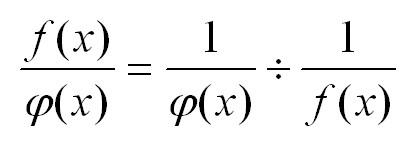
              Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:

              

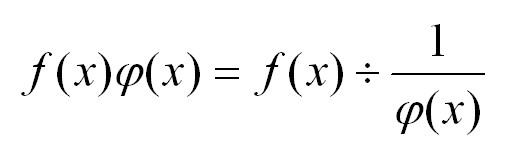
              Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:

              

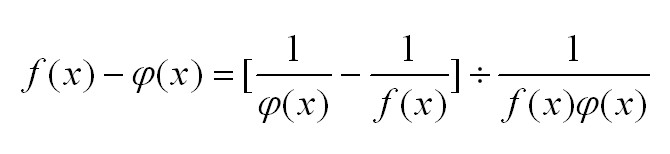
              Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:

              

              Теперь перейдем к примерам.

              Найти предел по правилу Лопиталя:

              

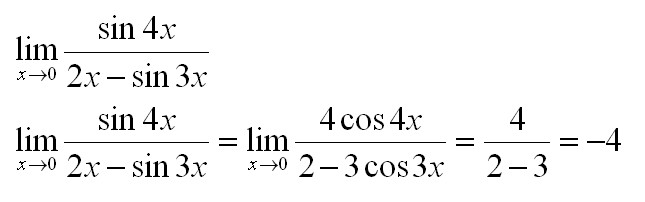
              Вычислить с использованием правила Лопиталя:

              

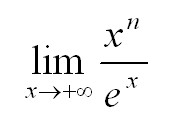
              Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.

              Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:

              

              

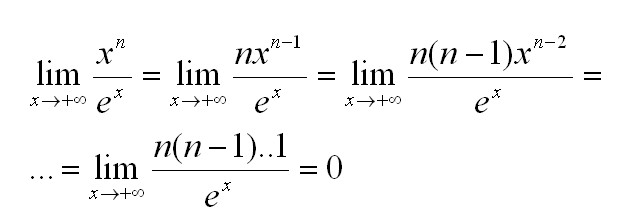
              Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

              zaochnik.ru

              Нахождение предела функции в точке по правилу Лопиталя

              Нахождение предела функции, по правилу Лопиталя, раскрывающий неопределённости вида 0/0 и ∞/∞.

              Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.

              

              Предел функции в точке — правило Лопиталя

              Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

              Точка в которой необходимо посчитать предел

              Правило Лопиталя

              Если выполняются следующие условия:

              • пределы функций f(x) и g(x) равны между собой и равны нулю или бесконечности:
                или ;
              • функции g(x) и f(x) дифференцируемы в проколотой окрестности a;
              • производная функции g(x) не равна нулю в проколотой окрестности a
              • и существует предел отношения производной f(x) к производной g(x):

              Тогда существует предел отношения функций f(x) и g(x):
              ,

              И он равен пределу отношения производной функции f(x) к производной функции g(x):

              В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:

              + — сложение
              — — вычитание
              * — умножение
              / — деление
              ^ — возведение в степень

              и следующих функций:

              • sqrt — квадратный корень
              • rootp — корень степени p, например root3(x) — кубический корень
              • exp — e в указанной степени
              • lb — логарифм по основанию 2
              • lg — логарифм по основанию 10
              • ln — натуральный логарифм (по основанию e)
              • logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
              • sin — синус
              • cos — косинус
              • tg — тангенс
              • ctg — котангенс
              • sec — секанс
              • cosec — косеканс
              • arcsin — арксинус
              • arccos — арккосинус
              • arctg — арктангенс
              • arcctg — арккотангенс
              • arcsec — арксеканс
              • arccosec — арккосеканс
              • versin — версинус
              • vercos — коверсинус
              • haversin — гаверсинус
              • exsec — экссеканс
              • excsc — экскосеканс
              • sh — гиперболический синус
              • ch — гиперболический косинус
              • th — гиперболический тангенс
              • cth — гиперболический котангенс
              • sech — гиперболический секанс
              • csch — гиперболический косеканс
              • abs — абсолютное значение (модуль)
              • sgn — сигнум (знак)

              planetcalc.ru