§ 182. Закон Бернулли
Как мы упоминали, в трубах не очень длинных и достаточно широких трение настолько невелико, что им можно пренебречь. При этих условиях падение давления так мало, что в трубе постоянного сечения жидкость в манометрических трубках находится практически на одной высоте. Однако, если труба имеет в разных местах неодинаковое сечение, то даже в тех случаях, когда трением можно пренебречь, опыт обнаруживает, что статическое давление в разных местах различно.
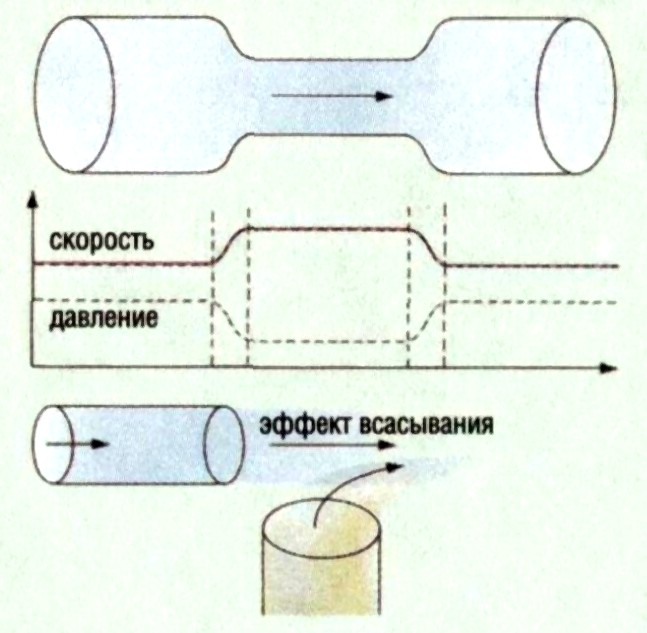
Возьмем трубу неодинакового сечения (рис. 311) и будем пропускать через нее постоянный поток воды. По уровням в манометрических трубках мы увидим, что в суженных местах трубы статическое давление меньше, чем в широких. Значит, при переходе из широкой части трубы в более узкую степень сжатия жидкости уменьшается (давление уменьшается), а при переходе из более узкой части в широкую — увеличивается (давление увеличивается).

Рис. 311. В узких частях трубы статическое давление текущей жидкости меньше, чем в широких
Это объясняется тем, что в широких частях трубы жидкость должна течь медленнее, чем в узких, так как количество жидкости, протекающей за одинаковые промежутки времени, одинаково для всех сечений трубы. Поэтому при переходе из узкой части трубы в широкую скорость жидкости уменьшается: жидкость тормозится, как бы натекая на препятствие, и степень сжатия ее (а также ее давление) растет. Наоборот, при переходе из широкой части трубы в узкую скорость жидкости увеличивается и сжатие ее уменьшается: жидкость, ускоряясь, ведет себя подобно распрямляющейся пружине.
Итак, мы видим, что давление жидкости, текущей по трубе, больше там, где скорость движения жидкости меньше, и обратно: давление меньше там, где скорость движения жидкости больше. Эту зависимость между скоростью жидкости и ее давлением называют законом Бернулли по имени швейцарского физика и математика Даниила Бернулли (1700—1782).
Закон Бернулли имеет место и для жидкостей и для газов. Он остается в силе и для движения жидкости, не ограниченного стенками трубы, — в свободном потоке жидкости. В этом случае закон Бернулли нужно применять следующим образом.
Допустим, что движение жидкости или газа не изменяется с течением времени (установившееся течение). Тогда мы можем представить себе внутри потока линии, вдоль которых происходит движение жидкости. Эти линии называются линиями тока; они разбивают жидкость на отдельные струи, которые текут рядом, не смешиваясь. Линии тока можно сделать видимыми, вводя в поток воды жидкую краску через тонкие трубочки. Струйки краски располагаются вдоль линий тока. В воздухе для получения видимых линий тока можно воспользоваться струйками дыма. Можно показать, что закон Бернулли применим для каждой струи в отдельности: давление больше в тех местах струи, где скорость в ней меньше и, следовательно, где сечение струи больше, и обратно. Из рис. 311 видно, что сечение струи велико в тех местах, где линии тока расходятся; там же, где сечение струи меньше, линии тока сближаются. Поэтому закон Бернулли можно сформулировать еще так: в тех местах потока, где линии тока гуще, давление меньше, а в тех местах, где линии тока реже, давление больше.
Возьмем трубу, имеющую сужение, и будем пропускать по ней с большой скоростью воду. Согласно закону Бернулли, в суженной части давление будет понижено. Можно так подобрать форму трубы и скорость потока, что в суженной части давление воды будет меньше атмосферного. Если теперь присоединить к узкой части трубы отводную трубку (рис. 312), то наружный воздух будет засасываться в место с меньшим давлением: попадая в струю, воздух будет уноситься водой. Используя это явление, можно построить разрежающий насос — так называемый водоструйный насос. В изображенной на рис. 313 модели водоструйного насоса засасывание воздуха производится через кольцевую щель 1, вблизи которой вода движется с большой скоростью. Отросток 2 присоединяется к откачиваемому сосуду. Водоструйные насосы не имеют движущихся твердых частей (как, например, поршень в обычных насосах), что составляет одно из их преимуществ.

Рис. 312. Воздух засасывается в узкую часть трубы, где давление меньше атмосферного

Рис. 313. Схема водоструйного насоса
Будем продувать воздух по трубке с сужением (рис. 314). При достаточной скорости воздуха давление в суженной части трубки будет ниже атмосферного. Жидкость из сосуда будет засасываться в боковую трубку. Выходя из трубки, жидкость будет распыляться струей воздуха. Этот прибор называется пульверизатором — распылителем.

Рис. 314. Пульверизатор
sfiz.ru
Школьная Энциклопедия
Login Form
Закон Бернулли в аэродинамике
Подробности Категория: Человек и небо Опубликовано 23.07.2014 16:59 Просмотров: 14379

Какое отношение к авиации имеет закон Бернулли? Оказывается, самое прямое. С его помощью можно объяснить возникновение подъёмной силы крыла самолёта и других аэродинамических сил.

Автор этого закона — швейцарский физик-универсал, механик и математик. Даниил Бернулли — сын известного швейцарского математика Иоганна Бернулли. В 1838 г. он опубликовал фундаментальный научный труд «Гидродинамика», в котором и вывел свой знаменитый закон.
Следует сказать, что в те времена аэродинамика как наука ещё не существовала. А закон Бернулли описывал зависимость скорости потока идеальной жидкости от давления. Но в начале ХХ века начала зарождаться авиация. И вот тут закон Бернулли оказался очень кстати. Ведь если рассматривать воздушный поток как несжимаемую жидкость, то этот закон справедлив и для воздушных потоков. С его помощью смогли понять, как поднять в воздух летательный аппарат тяжелее воздуха. Это важнейший законом аэродинамики, так как он устанавливает связь между скоростью движения воздуха и действующим в нём давлением, что помогает делать расчёты сил, действующих на летательный аппарат.
Закон Бернулли — это следствие закона сохранения энергии для стационарного потока идеальной и несжимаемой жидкости.
В аэродинамике воздух рассматривается как несжимаемая жидкость, то есть, такая среда, плотность которой не меняется с изменением давления. А стационарным считается поток, в котором частицы перемещаются по неизменным во времени траекториям, которые называют линиями тока. В таких потоках не образуются вихри.
Чтобы понять сущность закона Бернулли, познакомимся с уравнением неразрывности струи.
Уравнение неразрывности струи

Если жидкость течёт по трубе, имеющей разное поперечное сечение, то давление в разных местах трубы будет неодинаковое.
Мысленно выделим в трубе несколько сечений, обозначив их площади S1 и S2. Соответственно, v1 и v2 – скорости течений несжимаемой жидкости через эти сечения.
За время ∆t через сечения протекут жидкости, объёмы которых будут равны:
Так как мы рассматриваем стационарное течение несжимаемой жидкости, то по закону сохранения массы через любое поперечное сечение трубы за одинаковый промежуток времени проходит одинаковый объём жидкости. Следовательно, ∆V1 = ∆V2.
Произведение площади поперечного сечения потока на его скорость есть величина постоянная. Это уравнение называют уравнением неразрывности струи.
Уравнение Бернулли
Объединив условие неразрывности жидкости и закон сохранения энергии, Бернулли вывел уравнение, согласно которому с увеличение скорости потока уменьшается давление, и наоборот.
То есть, скорости жидкостей обратно пропорциональны площадям сечений. И чем больше площадь сечения, тем меньше скорость жидкости, протекающей через него, и наоборот.
Подобное явление мы видим, когда стоим на берегу реки и наблюдаем за её течением. В узком месте русла скорость течения воды всегда больше, чем в широком.
Жидкость, поступающая из широкой в более узкую часть трубы, ускоряется. Это означает, что на неё действует сила со стороны жидкости, находящейся в более широкой части трубы. Откуда же берётся эта сила? Для горизонтальной трубы причина возникновения этой силы — разность давлений в широком и узком участках трубы. В широкой части давление выше, чем в узкой, а скорость ниже. Отсюда следует вывод: «При стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и наоборот».
Уравнение Бернулли имеет вид:
где ρ – плотность жидкости,
ν – скорость потока,
h – высота, на которой располагается элемент жидкости,
ɡ — ускорение свободного падения,
p – давление в точке пространства, в которой расположен центр массы элемента жидкости.
Первое слагаемое уравнения Бернулли – кинетическая энергия потока, или динамическое давление. Его создаёт движение жидкости или газа. В авиации его также называют скоростным напором.
Второе слагаемое — потенциальная энергия, или гидростатическое давление. Оно создаётся весом столба жидкости или газа высотой h.
И, наконец, третье слагаемое, Р – это статистическое давление, которое оказывают друг на друга соседние слои жидкости или газа.
Сумма всех слагаемых уравнения называется полным давлением.
Для трубы, расположенной горизонтально, или горизонтального воздушного потока уравнение Бернулли выглядит так:

Из него видно, что чем выше скорость течения жидкости (а в аэродинамике – скорость воздушного потока), тем меньше давление, и наоборот.
Эффект Бернулли можно наблюдать, сидя у камина. Во время сильных порывов ветра скорость воздушного потока возрастает, а давление падает. В комнате давление воздуха выше. И языки пламени устремляются вверх в дымоход.
Закон Бернулли и авиация

С помощью этого закона очень просто объяснить, как возникает подъёмная сила для летательного аппарата тяжелее воздуха.
Во время полёта крыло самолёта как бы разрезает воздушный поток на две части. Одна часть обтекает верхнюю поверхность крыла, а другая нижнюю. Форма крыла такова, что верхний поток должен преодолеть больший путь для того, чтобы соединиться с нижним в одной точке. Значит, он двигается с большей скоростью. А раз скорость больше, то и давление над верхней поверхностью крыла меньше, чем под нижней. За счёт разности этих давлений и возникает подъёмная сила крыла.
Во время набора самолётом высоты возрастает разница давлений, а значит, увеличивается и подъёмная сила, что позволяет самолёту подниматься вверх.
Сразу сделаем уточнение, что вышеописанные законы действуют, если скорость движения воздушного потока не превышает скорость звука (до 340 м/с). Ведь мы рассматривали воздух как несжимаемую жидкость. Но оказывается, что при скоростях выше скорости звука воздушный поток ведёт себя по-другому. Сжимаемостью воздуха пренебрегать уже нельзя. И воздух в этих условиях, как любой газ, старается расшириться и занять больший объём. Появляются значительные перепады давления или ударные волны. А сам воздушный поток не сужается, а, наоборот, расширяется. Решением задач о движении воздушных потоков со скоростями, близкими или превышающими скорость звука, занимается газовая динамика, возникшая как продолжение аэродинамики.
Используя аэродинамические законы, теоретическая аэродинамика позволяет сделать расчёты аэродинамических сил, действующих на летательный аппарат. А правильность этих расчётов проверяют, испытывая построенную модель на специальных экспериментальных установках, которые называются аэродинамическими трубами. Эти установки позволяют измерить величину сил специальными приборами.
Кроме исследования сил, действующих на аэродинамические модели, с помощью аэродинамических измерений изучают распределение значений скорости, плотности и температуры воздуха, обтекающего модель.
ency.info
ЗАКОН БЕРНУЛЛИ
Научно-технический энциклопедический словарь .
Смотреть что такое «ЗАКОН БЕРНУЛЛИ» в других словарях:
Закон Бернулли — является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: Здесь плотность жидкости, скорость потока, высота, на которой находится рассматриваемый… … Википедия
ЗАКОН БЕРНУЛЛИ — один из основных законов гидродинамики, который связывает скорость потока идеальной несжимаемой жидкости и давление при установившемся течении. Согласно этому закону давление текущей жидкости больше в тех сечениях потока, в которых скорость его… … Большая политехническая энциклопедия
Бернулли, Даниил — Эта статья о физике и математике Данииле Бернулли. Другие представители семьи Бернулли и другие значения перечислены на странице Бернулли (семья). Даниил Бернулли нем. Daniel Bernoulli … Википедия
Бернулли Даниил — Даниил Бернулли Эта статья о физике и математике Данииле Бернулли. Другие представители семьи Бернулли перечислены на странице Бернулли (семья). Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 17 марта 1782), выдающийся швейцарский… … Википедия
Бернулли Д. — Даниил Бернулли Эта статья о физике и математике Данииле Бернулли. Другие представители семьи Бернулли перечислены на странице Бернулли (семья). Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 17 марта 1782), выдающийся швейцарский… … Википедия
Закон сохранения энергии — Закон сохранения энергии фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и… … Википедия
Закон Торричелли — Не следует путать с Формула Торричелли. Закон Торричелли, также известный как Теорема Торричелли, – это теорема в гидродинамике, связывающая скорость жидкости, вытекающей через отверстие, с высотой жидкости над отверстием. Закон Торричелли… … Википедия
Бернулли (семья) — У этого термина существуют и другие значения, см. Бернулли. Семья Бернулли (Bernoulli) швейцарская протестантская семья, многие члены которой в XVII XVIII веках внесли существенный вклад в науку. В частности, к этой династии принадлежат 9… … Википедия
Бернулли — (Bernoulli) фамилия. Семья Бернулли семья, многие члены которой внесли существенный вклад в науку. Из них наиболее известны: Бернулли, Якоб (1654 1708); Бернулли, Иоганн (1667 1748), младший брат Якоба; Бернулли, Даниил (1700 1782),… … Википедия
Закон Дарси — Механика сплошных сред … Википедия
dic.academic.ru

Гастро Паб в Кузьминках «Закон Бернулли»
Информация
О месте: Добро пожаловать в гастрономический паб «Закон Бернулли», мир крафтового пива в Кузьминках😃.
📢 24 крана разливного пива от лучших российских и зарубежных крафтовых пивоварен; Показать полностью…
📢 Более 50 сортов бутылочного пива и ассортимент постоянно меняется;
📢 Вкуснейшая еда и закуски от нашего шеф-повара и его команды.
🎤 По пятницам и субботам с 20.00 к нам приезжают cover группы, которые исполняют песни таких известных групп как: AC/DC, PinkFployd, Kiss, Deep Purple и др.
👑В нашем ресторане вы почувствуете себя не просто гостем, но и нашим другом.
🎉Каждый сотрудник ресторана, будь то управляющий или охранник, всегда рады поддержать беседу, помочь с выбором и даже рассказать анекдот. Веб-сайт: http://zakonbernulli.ru Дата основания: 7 декабря 2017
90 записей предложить новость

20 июля, в 21:00 представляем Mix Music Band.
Время расслабиться после рабочей недели и вспомнить русские и мировые поп хиты современности! 


Уже совсем скоро #пятница !
На этот раз она не простая, а магическая.☻
Это день волшебства и исполнения желаний.
А какое может быть #желание после рабочей недели?
Конечно же провести #вечер пятницы в тёплой компании за кружкой отменного пива, насладиться изысканной кухней,
послушать любимую музыку в исполнении группы ParadoX  и #потанцевать до упаду!
и #потанцевать до упаду!
vk.com
Закон бернул
Движение жидкости в замкнутой системе подчиняется закону Бернул-ли, который определяет, что жидкость перемещается из области более высокого давления в область более низкого давления. Исходя из этого, можно заключить, что движущей силой венозного притока является градиент среднего системного давления и давления в правом предсердии.
В физиологии кровообращения под средним системным давлением в сердечно-сосудистой системе понимается давление, которое устанавливается в условиях прекращения кровотока (остановка сердечной деятельности), после того, как перераспределение крови между артериями, капиллярами и венами приведет к выравниванию давления во всех сегментах соответствующего круга кровообращения. Иначе говоря, среднее системное давление отражает усредненный уровень давлений во всех сегментах сердечно-сосудистой системы.
Величина среднего давления в каждом сегменте сердечно-сосудистой системы зависит от его емкости, под которой понимается объем крови, находящейся в этом сегмент при данном уровне давления и описывается следующим отношением:
С = V/P, где
С — емкость сосудистого русла;
V — изменение объема крови;
Р — изменение давления.
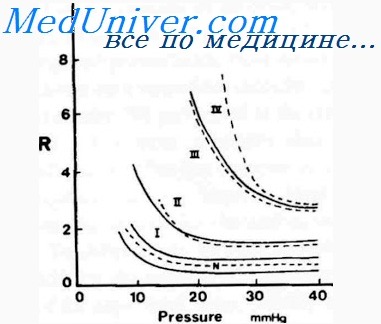
Отсюда следует, что при изменении емкости сосудистого русла будет изменяться и среднее системное давление. Чем больше емкость сосудистого русла, тем меньше будет возрастать системное давление при увеличении в нем объема крови. Специальными исследованиями было установлено, что емкость венозного русла в 18 раз больше артериального.
Поэтому венозное русло может депонировать значительные количества крови без существенного повышения в нем давления, а даже незначительный прирост объема крови в артериальной системе неизбежно приведет к возрастанию системного давления. Следовательно, среднее системное давление в сердечно-сосудистой системе представляет собой усредненную величину емкости артериального и венозного русла.
К сожалению, определить среднее системное давление можно только в эксперименте, т.к. для этого необходима остановка сердца. Однако известно, что основные гемодинамические функции у животного (собаки) и человека существенно не различаются и закономерности, установленные в эксперименте, подтверждаются при исследованиях, проведенных у человека при операциях на сердце в условиях искусственного кровообращения.
В связи с этим данные, полученные в эксперименте, в частности относительно закономерностей венозного притока, могут быть с достаточной степенью вероятности экстраполированы на человека.
Так было установлено, что нормальные величины среднего системного давления в большом и малом круге кровообращения различаются незначительно и составляют соответственно 7 мм Нд для большого и 5 мм Нд для малого круга кровообращения. Следовательно, в нормальных условиях (при отсутствии патологии гемодинамики) градиент давлений, обеспечивающий венозный приток, составляет 7-10 мм Нд. И именно в этом диапазоне давлений реализуются нормальный венозный приток и сердечный выброс.
meduniver.com
