Закон джоуля ленца можно записать

Величина, обратная удельному сопротивлению, называется удельной электропроводностью:

В этом случае применяется закон Джоуля — Ленца в виде

Введем понятие удельной мощности электрического тока – это мощность, выделяющаяся в единице объема проводника за единицу времени:

E — напряженность электрического поля в проводнике.

Проводник может нагреваться, в этом случае энергия электрического поля превращается в тепло.

Сопротивление участка цепи можно записать в виде

Количество теплоты, выделяющейся в проводнике, равно произведению квадрата силы тока на сопротивление проводника и на время протекания электрического тока:

Закон Джоуля — Ленца для участка цепи

Ленц Эмилий Христианович (1804 – 1865), русский физик, родился в Дерпте (Тарту). Учился в Дерптском ун-те.

Установил зависимость количества тепла, выделяющегося в проводнике, от величины тока и сопротивления проводника.

Джоуль Джеймс Прескотт (1818 – 1889), английский физик, родился в Солфорде. Получил домашнее образование.

Таким образом, работа, совершаемая электрическим током, может быть записана в виде

больше, чем количество тепла , выделяющееся в проводнике сопротивлением

В результате опытов физики заметили, что при подключении проводника к электропитанию начинает выделяться тепло.

Знаменитый закон Лжоуля Ленца можно описать формулой:

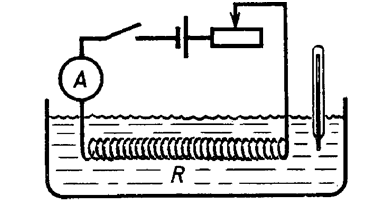
Воспроизведение опытов, с помощью которых была сформулирована закономерность Джоуля-Ленца

Оба физика проводили множество экспериментов, в которых главным действующим прибором был калориметр. Агрегат представлял собой устройство, изолированное от теплопотерь, у которого была измерена и зафиксирована теплоемкость. Калориметр был оснащен термометром, в него также вставлялся проводник с определенным электросопротивлением.

Закон Джоуля Ленца

Основываясь на этом выводе, можно представить тепловую закономерность Джоуля Ленца в несколько другом виде, а именно в ее интегральном и дифференциальном видах.

работают лишь при определенных условиях, и их нельзя считать законом.

Закон Джоуля Ленца в интегральной и дифференциальной формах

Работа тока на подключенном участке преобразовывает электроэнергию во внутреннюю. Это происходит за счет того, что свободные электроны натыкаются на нейтральные молекулы (лишенные электронов) проводника, и присущая им механическая энергия превращается в тепловую. Она способствует увеличению температуры проводника. Согласуясь со всемирным законом сохранения энергии, тот объем тепла (q) приравнивается к работе тока.

Обратите внимание! Поскольку тепло всегда вырабатывается в проводнике, находящемся под электрическим током, может случиться его перегрев и, как следствие, выход из строя электрических устройств. Особенно опасным явлением является короткое замыкание, когда сопротивление проводников стремится к нулю, ток становится очень сильным, соответственно, выделяется огромное количество тепла, приводящее к аварийным состояниям.

После открытия М. Фарадеем явления электромагнитной индукции он и ряд других ученых предложили мнемонические и довольно сложные «правила», позволяющие в частных случаях определять направление индуктированного тока.

Эмилий Христианович Ленц родился (12) 24 февраля 1804 г. в семье обер-секретаря магистрата г. Тарту (Эстония). Этот город был основан в 1030 г. русским князем Ярославом Мудрым и назывался Юрьевом. После захвата прибалтийских земель немецкими крестоносцами город переименовали в Дерпт. Так он назывался почти до конца XIX в. (хотя и был возвращен России), а затем – как и в нотца семья оказалась в тяжелом материальном положении и матери Ленца пришлось приложить немало усилий, чтобы дать двум сыновьям высшее образование.

Труды Ленца, печатавшиеся в отечественных и зарубежных изданиях, были широко известны среди физиков всего мира. С ними был хорошо знаком и Б.С. Якоби, еще до приезда в Россию построивший оригинальную модель электродвигателя.

Выдающиеся заслуги Э.Х. Ленца в области геофизики и электродинамики получили всеобщее признание и высокую оценку Академии наук: в сентябре 1834 года он избирается в число ординарных академиков по физике.

Баллистический метод измерения Ленца лежит в основе современного баллистического гальванометра. Вочного прибора для измерения переменных токов – электродинамометра Вебера, что позволило Ленцу еще в 30-х годах сделать ряд важнейших открытий.

Не существовало точных приборов и методов измерения электрических и магнитных величин, в частности индуктированных токов. Не было закона о направлении этих токов, не были установлены и количественные характеристики явления электромагнитной индукции.

Закон Ленца был установлен за восемь лет до опубликования первой работы немецкого ученого Р. Майера, который считается одним из основоположников закона сохранения и превращения энергии. Поэтому Ленцу принадлежит заслуга в закладке основ этого фундаментального закона природы. В 1845 г. немецкий физик Ф. Нейман впервые математически сформулировал теорию индукции и предложил выражение для электродвижущей силы индукции, подтверждающее закон Ленца.

Действительно, если перемещать под действием внешней силы магнит или проводник с током вблизи замкнутого проводникаическая энергия перемещения магнита или проводника с током превращается в электромагнитную энергию тока индукции.

Заслуга Ленца заключается не только в том, что он сформулировал общий закон о направлении индуктированного тока, но и – что не менее важно – убедительно доказал справедливость закона сохранения и превращения энергии при взаимных превращениях механической и электромагнитной энергии. (Термин «энергия» впервые был введен в 1853 г. английским ученым Ренкиным.)

Закон Ленца (стр

Заметим, что издатель известного в те годы журнала «Poggеndorff’s Annalen» не рискнул опубликовать столь необычные и смелые выводы Ленца, они были напечатаны в мемуарах Академии наук (1833).

После открытия Фарадея многие явления, связанные с электромагнитной индукцией, оставались недостаточно ясными.

Первым важнейшим изобретением Ленца была разработка баллистического метода измерений для изучения законов индукции. В 1832 г., узнав об открытии Фарадеем явления электромагнитной индукции, Ленц приступил к экспериментам с целью установления количественных законов индукции. Он считал, что «сила мгновенного тока индукции» действует подобно удару, причем сила этого удара может быть измерена по скорости, сообщаемой стрелке мультипликатора – единственного в то время индикатора электрического тока.

Кроме того, Эмилий Ленц и английский учёный-физик Джоуль, изучая на опыте тепловые действия тока, независимо один от другого открыли закон, согласно которому количество теплоты, которое выделяется в проводнике, будет прямо пропорционально квадрату электрического тока, который проходит по проводнику, его сопротивлению и времени, в течение которого электрический ток поддерживается неизменным в проводнике.

Закон Джоуля — Ленца (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) — закон, дающий количественную оценку теплового действия электрического тока.

Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время dt через сечение проводника переносится заряд dq = Idt. Так как ток представляет собой перемещение заряда dq под действием электрического поля, то, по формуле (84.6), работа тока

При протекании тока по проводнику происходит превращение электрической энергии в тепловую, причём количество выделенного тепла будет равно работе электрических сил:

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

В системе единиц СИ энергия, количество теплоты и работа измеряются единицами – джоулями. Поэтому коэффициент пропорциональности в законе Джоуля – Ленца равен единице. В этой системе формула Джоуля – Ленца имеет вид:

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

Закон джоуля ленца формула и определение

Выражение (99.5) представляет собой закон Джоуля — Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем[1].

Если соединить три одинаковой толщины проволоки – медную, железную и никелиновую – параллельно между собой и пропустить через них ток, то наибольшее количество теплоты выделится в медной проволоке, она и нагреется сильнее остальных.

Эмилий Христианович Ленц (1804 — 1865) – русский знаменитый физик. Он является одним из основоположников электромеханики. С его именем связано открытие закона, определяющего направление индукционного тока, и закона, определяющего электрическое поле в проводнике с током.

Формулы (99.6) и (99.7) являются обобщенным выражением закона Джоуля — Ленца в дифференциальной форме, пригодным для любого проводника.

Таким образом, используя выражения (99.4), (99.1) и (99.2), получим

где t — время свободного пробега, которое можно найти по формуле , так как .

Выведем закон Ома для металлов, исходя из модели электронного газа.

где называется удельной электропроводностью металла. Обратная ей величина называется удельным сопротивлением.

Будем считать, что в начале свободного пробега, сразу после соударения, cкорость направленного движения электрона u = 0. К концу свободного пробега его скорость становится равной u_max. Электрон приобретает кинетическую энергию

Законы Ома и Джоуля-Ленца в дифференциальной форме

Полученное соотношение (10) представляет собой математическое выражение закона Джоуля-Ленца в дифференциальной форме: количество теплоты, выделившееся в единице объема проводника при протекании тока в единицу времени (тепловая мощность), пропорционально квадрату напряженности поля.

С учетом последнего, (9) можно переписать так . (10)

Множитель при Е 2 есть не что иное, как удельная проводимость .

где n – число электронов в единице объема – концентрация электронов.

где n – концентрация свободных электронов.

Найдем среднюю скорость дрейфа , применяя к электрону II закон Ньютона

Каждый электрон испытывает за 1 секунду z соударений ; сообщая всякий раз решетке энергию (8).

Для подсчета заряда, переносимого через площадку S, выберем параллелепипед с основанием S = 1 м 2 (рисунок 2). Число электронов, заключенных в объеме V параллелепипеда длиной , будет равно числу N электронов, пересекающих площадку S = 1м 2 в 1 с: (S = 1),

A = – Q, т.е. работа тока полностью переходит в тепло.

Если обратить внимание на величину, представляющую разность внутренней энергии проводника за время прохождения по нему тока, можно заметить, что постепенно при нагревании эта энергия будет увеличиваться. Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:

Российский и английский ученые пришли к выводу, что количество теплоты q, получаемое в полупроводнике при прохождении постоянного тока, прямо пропорционально величине тока (I), возведенной во вторую степень, и тому времени (t), что ток пропускался по проводнику, испытывая сопротивление (R).

Опыты Ленца более точные. Он определил, что открытая им закономерность не действует, если проводники двигаются, когда через них течет электроток (они называются проводники второго типа), такие как индуктивная катушка, находящаяся внутри электромотора.

Формула интегрального закона Джоуля-Ленца справедлива при любых данных, поэтому она считается законом. Другие же формулировки типа:

Всякое преодоление сопротивления неизбежно сопровождается затратами энергии. Если, к слову, что-то тяжелое приходится тянуть, преодолевая силу трения, то работа по ее преодолению становится теплом. В случае с током и полупроводником электросопротивление выступает в роли трения.

Открытие двух знаменитых физиков стало заметной вехой на пути к исследованию и всемирному принятию закона сохранения энергии. Благодаря ему, сегодня общеизвестно, что и тепло, и электроток, и движение механических частиц – есть формы материи, обладающие своей энергией, которую можно измерить. Закон Джоуля-Ленца (и последующие работы Джоуля) помогли установить соответствия для электрического, механического и теплового вида энергии и определить переводные соотношения между единицами различных видов (калории и джоули). Тепловая закономерность применяется и в разработке теории тока в металлах.

Джоуль проводил эти исследования в рамках изучения закона сохранения энергии. Он хотел оценить, какова величина механической энергии, давшей полученное количество теплоты. Для этого к динамо-машине, вращавшей ротор для выработки электричества, он привязывал некий груз и делал вывод, что разница между механической энергией груза в поле и вне поля тяготения и есть искомая величина. Англичанин доказал, что сделанные им выводы о преобразовании энергии применимы и для электролитических растворов.

pahomova-nsk.ru

Закон Джоуля-Ленца: его формулировка и применение

Формулировка

В реальном проводнике при протекании через него тока выполняется работа против сил трения. Электроны движутся через провод и сталкиваются с другими электронами, атомами и прочими частицами. В результате этого выделяется тепло. Закон Джоуля-Ленца описывает количество тепла, выделяемое при протекании тока через проводник. Оно прямо пропорционально зависит от силы тока, сопротивления и времени протекания.

В интегральной форме Закон Джоуля-Ленца выглядит так:

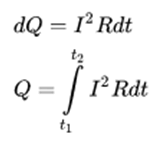
Сила тока обозначается буквой I и выражается в Амперах, Сопротивление — R в Омах, а время t — в секундах. Единица измерения теплоты Q — Джоуль, чтобы перевести в калории нужно умножить результат на 0,24. При этом 1 калория равна количеству теплоты, которое нужно подвести к чистой воде, чтобы увеличить её температуру на 1 градус.

Такая запись формулы справедлива для участка цепи при последовательном соединении проводников, когда в них протекает одна величина тока, но падает на концах различное напряжение. Произведение силы тока в квадрате на сопротивление равняется мощности. В то же время мощность прямо пропорциональна квадрату напряжения и обратно пропорциональна сопротивлению. Тогда для электрической цепи при параллельном соединении можно Закон Джоуля-Ленца можно записать в виде:

В дифференциальной форме он выглядит следующим образом:

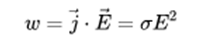
Где j — плотность тока А/см 2 , E — напряженность электрического поля, сигма — удельное сопротивление проводника.

Стоит отметить что для однородного участка цепи сопротивление элементов будет одинаковым. Если в цепи присутствуют проводники с разным сопротивлением возникает ситуация, когда максимальное количество тепла выделяется на том, который имеет самое большое сопротивление, о чем можно сделать вывод, проанализировав формулу Закона Джоуля-Ленца.

Частые вопросы

Как найти время? Здесь имеется в виду период протекания тока через проводник, то есть когда цепь замкнута.

Как найти сопротивление проводника? Для определения сопротивления используют формулу, которую часто называют “рельс”, то есть:

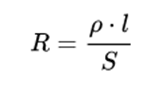
Здесь буквой «Ро» обозначается удельное сопротивление, оно измеряется в Ом*м/см2, l и S это длина и площадь поперечного сечения. При вычислениях метры и сантиметры квадратные сокращаются и остаются Омы.

Удельное сопротивление — это табличная величина и для каждого металла она своя. У меди на порядки меньше, чем у высокоомных сплавов типа вольфрама или нихрома. Для чего это применяется мы рассмотрим ниже.

Перейдем к практике

Закон Джоуля-Ленца имеет большое значение для электротехнических расчетов. В первую очередь вы можете его применить при расчете нагревательных приборов. В качестве нагревательного элемента чаще всего применяется проводник, но не простой (типа меди), а с высоким сопротивлением. Чаще всего это нихром или кантал, фехраль.

Они имеют большое удельное сопротивление. Вы можете использовать и медь, но тогда вы потратите очень много кабеля (сарказм, медь не используют в этих целях). Чтобы рассчитать мощность тепла для нагревательного прибора вам нужно определится, какое тело и в каких объемах вам нужно нагреть, учесть количество требуемой теплоты и за какое время её нужно передать телу. После расчетов и преобразований вы получите сопротивление и силу тока в этой цепи. На основании полученных данных по удельному сопротивлению подбираете материал проводника, его сечение и длину.

Закон Джоуля-Ленца при передаче электричества на расстояние

При передаче электроэнергии на расстояния возникает существенная проблема — потери на линиях передачи (ЛЭП). Закон Джоуля-Ленца описывает количество тепла, выделенного проводником при протекании тока. ЛЭП питают целые предприятия и города, а для этого нужна большая мощность, как следствие большой ток. Так как количество теплоты зависит от сопротивления проводника и тока, чтобы кабеля не грелись нужно уменьшить количество тепла. Увеличить сечение проводов не всегда можно, т.к. это затратно в плане стоимости самой меди и веса кабеля, что влечет за собой удорожание несущей конструкции. Высоковольтные линии электропередач изображены ниже. Это массивные металлоконструкции, созданные чтобы поднять кабеля на безопасную высоту над землей, с целью избежания поражения электрическим током.

Поэтому нужно снизить ток, чтобы это сделать повышают напряжение. Между городами линии электропередач обычно имеют напряжение 220 или 110 кВ, а у потребителя понижается до нужной величины с помощью трансформаторных подстанций (КТП) или целым рядом КТП постепенно понижая до более безопасных для передачи величин, например 6 кВ.

Таким образом при той же потребляемой мощности при напряжении в 380/220 В ток снизится в сотни и тысячи раз ниже. А по закону Джоуля-Ленца количество тепла в этом случае определяется мощностью, которая теряется на кабеле.

Плавкие вставки и предохранители

Закон Джоуля-Ленца применяется при расчете плавких предохранителей. Это такие элементы, которые защищают электрическое или электронное устройство от чрезмерных для него токов, которые могут возникнуть в следствии скачка питающего напряжения, короткого замыкания на плате или обмотках (в случае двигателей) для защиты от дальнейших разрушений электрической системы в целом и пожара. Они состоят из корпуса, изолятора и тонкой проволоки. Проволока подбирается таким сечением, чтобы номинальный ток через нее протекал, а при его превышении количество выделяемого тепла при этом пережигало её.

В результате выше описанного сделаем вывод, что Закон Джоуля-Ленца нашел широчайшее применение и очень важен для электротехники. Благодаря информации о количеству теплоты, которую даёт выполнение расчетов по формулам указанным выше, мы можем узнать о режимах работы устройств, подобрать необходимые материалы и сечение для повышения безопасности, надежности и долговечности прибора или цепи в целом.

На этом мы и заканчиваем нашу статью. Надеемся, предоставленная информация была для вас полезной и интересной. Напоследок рекомендуем просмотреть видео, на котором более подробно рассматривается данный вопрос:

Наверняка вы не знаете:

samelectrik.ru

Линейные уравнения. ОГЭ по математике

Работа состоит из трех модулей: «Алгебра», «Геометрия», «Реальная математика». В модули «Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровнях, в модуль «Реальная математика» — одна часть, соответствующая проверке на базовом уровне.

При проверке базовой математической компетентности учащиеся должны продемонстрировать: владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.

Части 2 модулей «Алгебра» и «Геометрия» направлены на проверку владения материалом на повышенном уровне. Их назначение — дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, составляющую потенциальный контингент профильных классов.

Эти части содержат задания повышенного уровня сложности из различных разделов курса математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности — от относительно более простых до сложных, предполагающих свободное владение материалом курса и хороший уровень математической культуры.

Содержимое разработки

1. Длину окруж­но­сти можно вы­чис­лить по фор­му­ле , где — ра­ди­ус окруж­но­сти (в мет­рах). Поль­зу­ясь этой фор­му­лой, най­ди­те ра­ди­ус окруж­но­сти, если её длина равна 78 м. (Счи­тать ).

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)

2. Пло­щадь ромба можно вы­чис­лить по фор­му­ле , где — диа­го­на­ли ромба (в мет­рах). Поль­зу­ясь этой фор­му­лой, най­ди­те диа­го­наль , если диа­го­наль равна 30 м, а пло­щадь ромба 120 м 2 .

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 3)

3. Пло­щадь тре­уголь­ни­ка можно вы­чис­лить по фор­му­ле , где — сто­ро­на тре­уголь­ни­ка, — вы­со­та, про­ве­ден­ная к этой сто­ро­не (в мет­рах). Поль­зу­ясь этой фор­му­лой, най­ди­те сто­ро­ну , если пло­щадь тре­уголь­ни­ка равна , а вы­со­та равна 14 м.

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)

4. Пло­щадь тра­пе­ции можно вы­чис­лить по фор­му­ле , где — ос­но­ва­ния тра­пе­ции, — вы­со­та (в мет­рах). Поль­зу­ясь этой фор­му­лой, най­ди­те вы­со­ту , если ос­но­ва­ния тра­пе­ции равны и , а её пло­щадь .

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)

5. Ра­ди­ус впи­сан­ной в пря­мо­уголь­ный тре­уголь­ник окруж­но­сти можно найти по фор­му­ле , где и — ка­те­ты, а — ги­по­те­ну­за тре­уголь­ни­ка. Поль­зу­ясь этой фор­му­лой, най­ди­те , если и .

Источник: ГИА-2013. Математика. Московская обл. Пробные варианты(2 вар)

6. Объём пи­ра­ми­ды вы­чис­ля­ют по фор­му­ле , где — пло­щадь ос­но­ва­ния пи­ра­ми­ды, — её вы­со­та. Объём пи­ра­ми­ды равен 40, пло­щадь ос­но­ва­ния 15. Чему равна вы­со­та пи­ра­ми­ды?

Источник: ГИА-2013. Математика. Тренировочная работа № 3. (1 вар)

7. Пло­щадь лю­бо­го вы­пук­ло­го че­ты­рех­уголь­ни­ка можно вы­чис­лять по фор­му­ле , где — длины его диа­го­на­лей, а угол между ними. Вы­чис­ли­те , если .

Источник: ГИА-2012. Математика. Диагностическая работа № 1(2 вар)

8. Чтобы пе­ре­ве­сти зна­че­ние тем­пе­ра­ту­ры по шкале Цель­сия (t °C) в шкалу Фа­рен­гей­та (t °F), поль­зу­ют­ся фор­му­лой F = 1,8C + 32 , где C — гра­ду­сы Цель­сия, F — гра­ду­сы Фа­рен­гей­та. Какая тем­пе­ра­ту­ра по шкале Цель­сия со­от­вет­ству­ет 6° по шкале Фа­рен­гей­та? Ответ округ­ли­те до де­ся­тых.

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 01.10.2013 ва­ри­ант МА90105.

9. Цен­тро­стре­ми­тель­ное уско­ре­ние при дви­же­нии по окруж­но­сти (в м/c 2 ) можно вы­чис­лить по фор­му­ле где — уг­ло­вая ско­рость (в с −1 ), а R — ра­ди­ус окруж­но­сти. Поль­зу­ясь этой фор­му­лой, най­ди­те рас­сто­я­ние R (в мет­рах), если уг­ло­вая ско­рость равна 3 с −1 , а цен­тро­стре­ми­тель­ное уско­ре­ние равно 45 м/c 2 .

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.11.2013 ва­ри­ант МА90201.

10. Из за­ко­на все­мир­но­го тя­го­те­ния вы­ра­зи­те массу и най­ди­те её ве­ли­чи­ну (в ки­ло­грам­мах), если и гра­ви­та­ци­он­ная по­сто­ян­ная

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.11.2013 ва­ри­ант МА90202.

11. Пол­ную ме­ха­ни­че­скую энер­гию тела (в джо­у­лях) можно вы­чис­лить по фор­му­ле где — масса тела (в ки­ло­грам­мах), — его ско­рость (в м/с), — вы­со­та по­ло­же­ния цен­тра масс тела над про­из­воль­но вы­бран­ным ну­ле­вым уров­нем (в мет­рах), а — уско­ре­ние сво­бод­но­го па­де­ния (в м/с 2 ). Поль­зу­ясь этой фор­му­лой, най­ди­те (в мет­рах), если а

Источник: МИОО: Тре­ни­ро­воч­ная работа по ма­те­ма­ти­ке 19.02.2014 ва­ри­ант МА90501.

12. Мощ­ность по­сто­ян­но­го тока (в ват­тах) вы­чис­ля­ет­ся по фор­му­ле P = I 2 R, где I — сила тока (в ам­пе­рах), R — со­про­тив­ле­ние (в омах). Поль­зу­ясь этой фор­му­лой, най­ди­те со­про­тив­ле­ние R (в омах), если мощ­ность со­став­ля­ет 150 ватт, а сила тока равна 5 ам­пе­рам.

13. Ав­то­мо­биль про­ехал 200 ки­ло­мет­ров и из­рас­хо­до­вал при этом a лит­ров бен­зи­на. Сколь­ко лит­ров бен­зи­на по­тре­бу­ет­ся, чтобы про­ехать 37 ки­ло­мет­ров при таких же усло­ви­ях езды? За­пи­ши­те со­от­вет­ству­ю­щее вы­ра­же­ние.

14. Закон Ку­ло­на можно за­пи­сать в виде где — сила вза­и­мо­дей­ствия за­ря­дов (в нью­то­нах), и — ве­ли­чи­ны за­ря­дов (в ку­ло­нах), — ко­эф­фи­ци­ент про­пор­ци­о­наль­но­сти (в Н·м 2 /Кл 2 ), а — рас­сто­я­ние между за­ря­да­ми (в мет­рах). Поль­зу­ясь фор­му­лой, най­ди­те ве­ли­чи­ну за­ря­да (в ку­ло­нах), если Н·м 2 /Кл 2 , Кл, м, а Н.

15. Закон все­мир­но­го тя­го­те­ния можно за­пи­сать в виде где — сила при­тя­же­ния между те­ла­ми (в нью­то­нах), и — массы тел (в ки­ло­грам­мах), — рас­сто­я­ние между цен­тра­ми масс (в мет­рах), а — гра­ви­та­ци­он­ная по­сто­ян­ная, рав­ная 6.67 · 10 −11 H·м 2 /кг 2 . Поль­зу­ясь фор­му­лой, най­ди­те массу тела (в ки­ло­грам­мах), если Н, кг, а м.

16. Закон Джо­у­ля–Ленца можно за­пи­сать в виде Q = I 2 Rt, где Q — ко­ли­че­ство теп­ло­ты (в джо­у­лях), I — сила тока (в ам­пе­рах), R — со­про­тив­ле­ние цепи (в омах), а t — время (в се­кун­дах). Поль­зу­ясь этой фор­му­лой, най­ди­те время t (в се­кун­дах), если Q = 2187 Дж, I = 9 A, R = 3 Ом.

17. Пло­щадь четырёхуголь­ни­ка можно вы­чис­лить по фор­му­ле где и — длины диа­го­на­лей четырёхуголь­ни­ка, — угол между диа­го­на­ля­ми. Поль­зу­ясь этой фор­му­лой, най­ди­те длину диа­го­на­ли если a

18. Закон Мен­де­ле­е­ва-Кла­пей­ро­на можно за­пи­сать в виде PV = νRT, где P — дав­ле­ние (в пас­ка­лях), V — объём (в м 3 ), ν — ко­ли­че­ство ве­ще­ства (в молях), T — тем­пе­ра­ту­ра (в гра­ду­сах Кель­ви­на), а R — уни­вер­саль­ная га­зо­вая по­сто­ян­ная, рав­ная 8,31 Дж/(К⋅моль). Поль­зу­ясь этой фор­му­лой, най­ди­те тем­пе­ра­ту­ру T (в гра­ду­сах Кель­ви­на), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м 3 .

videouroki.net