Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Правило Хунда. Последовательность заполнения электронных состояний в пределах подгруппы, т. е. при одном и том же /, определяется правилом Хунда [c.285]

Второе правило Хунда дает наилучший подход для модельных расчетов. Например, Полинг и Уилсон проводят в своей книге [8] расчет спектральных термов, связанных с конфигурацией /7 . Третье правило Хунда есть следствие знака спин-орбитального взаимодействия. Для отдельного электрона энергия является наименьшей, когда его спин антипараллелен направлению орбитального момента количества движения. Однако пары с квантовыми числами niL, ms, отвечающие наинизшей энергии, по мере заполнения оболочки электронами постепенно исчерпываются согласно принципу Паули, когда оболочка заполнена более чем наполовину, состояние наинизшей энергии с необходимостью имеет спиновый момент, антипараллельный орбитальному. [c.525]

Рассмотрим два примера применения правил Хунда. [c.525]

Если два рассматриваемых состояния представляют собой состояния свободного атома, величина J имеет тенденцию быть положительной. Спины стремятся стать параллельными, как этого требует правило Хунда. Если взаимодействуют два состояния различных атомов, то величина J имеет тенденцию быть отрицательной. Это [c.524]

ОСНОВНОЕ СОСТОЯНИЕ ИОНОВ С ЧАСТИЧНО ЗАПОЛНЕННЫМИ ОБОЛОЧКАМИ. ПРАВИЛА ХУНДА [c.265]

Первое правило Хунда. Из множества состояний, которые можно образовать, размещая п электронов по 2 (2 + 1) уровням, наинизшей энергией обладает состояние с максимальным значением суммарного спина 5, допускаемым принципом Паули. Чтобы найти, каково это значение, отметим, что максимальное значение спина 8 равно максимальной величине компоненты спина 8 Если п О — состояние с минимальным значением J (орбитальный момент антипараллелен спиновому). Оказывается, что параметр 1 положителен для оболочек, заполненных менее чем наполовину, и отрицателен для оболочек, заполненных более чем наполовину. В результате состояния с наименьшей энергией характеризуются следуюпщми значениями / [c.266]

Расщепление в кристаллическом поле несущественно для редкоземельных ионов, потому что их частично заполненные 4/-оболочки лежат глубоко внутри иона (ниже заполненных 5 — и 5р-оболочек). В отличие от этого частично заполненные оболочки ионов переходных металлов находятся дальше всего от ядра и поэтому гораздо сильнее подвержены влиянию кристаллического окружения. На электроны частично заполненных -оболочек действует заметное электрическое поле, которое обладает не сферической симметрией, а только симметрией, отвечающей положению узла кристаллической решетки, в котором находится данный ион. Поэтому правила Хунда отчасти теряют свою силу. [c.273]

Оказывается, что первые два правила Хунда могут остаться справедливыми даже при учете влияния кристаллического окружения. Необходимо, однако, рассматривать кристаллическое поле как возмущение, действующее на (25 4- 1) 2Ь -Ь 1)-мерное множество состояний, определяемое первыми двумя правилами. Это возмущение добавляется к спин-орбитальному взаимодействию. Поэтому третье правило Хунда (которое обусловлено только спин-орбитальным взаимодействием) должно быть изменено. [c.273]

Для ионов переходных металлов из других периодов таблицы Менделеева (имеющих частично заполненные Ы- или 5й-оболочки) ситуация оказывается более сложной, поскольку в ионах тяжелых элементов спин-орбитальное взаимодействие имеет большую величину. Расщепление мультиплета за счет спин-орбитального взаимодействия может быть сравнимо с расщеплением в кристаллическом поле (или даже больше его). В подобных случаях рассмотрение перераспределения уровней в кристаллическом поле с образованием структур, отличных от тех, которые следуют из правил Хунда, основывается на применении весьма тонких методов теории групп. Мы не будем проводить здесь это рассмотрение, но укажем два важных принципа. [c.275]

Обычно из числа основных источников магнитного взаимодействия можно исключить и спин-орбитальное взаимодействие. Оно, несомненно, весьма важно для определения полного магнитного момента отдельных атомов и, следовательно, дает существенный вклад во внутриатомное магнитное взаимодействие. Однако даже в этом случае первые два правила Хунда (стр. 266) основаны исключительно на учете электростатической энергии. Только третье правило, определяющее окончательное расщепление -мультиплета, основано на учете спин-орбитального взаимодействия. Одпако в тех парамагнитных диэлектриках, где орбитальные моменты заморожены из-за расщепления уровней в кристаллическом поле (стр. 273), все же чисто электростатические эффекты подавляют эффекты, обусловленные спин-орбитальной связью. [c.288]

Чтобы понять происхождение ферромагнетизма, рассмотрим случай никеля с атомной конфигурацией 3d4s . В свободном атоме выполняются правила Хунда [1] ), и первая половина зоны заполнена З -электронами с параллельными спинами. Это результат обменного взаимодействия, которое в этом случае обеспечивает минимум электростатической энергии другими словами, электроны, описываемые симметричными волновыми функциями, стремятся расположиться в пространстве как можно дальше друг от друга, и, таким образом, электростатическая энергия уменьшается. Если вследствие высокой плотности состояний в d-зоне поверхность Ферми окажется в середине зоны проводимости, то можно ожидать, что заполнение состояний будет иметь вид, показанный на фиг. 49, а. Если, однако, обменное взаимодействие действует так же, как в свободном атоме, то будет заполняться половина d-зоны с отрицательной проекцией спина это иллюстрирует фиг. 49, б (энергия половины зоны с отрицательной проекцией спина меньше энергии половины с положительной проекцией). Таким образом, даже при отсутствии внешнего магнитного поля спины не сбалансированы, и металл оказывается ферромагнитным. [c.124]

Как известно, переходные металлы, испарение карбидов которых исследовалось, относятся к группе химических элементов, имеющих в состоянии изолированного атома недостроенные -электронные уровни. Как следует из правила Хунда, для -оболочки изолированного атома особо устойчивым является полузаполненное состояние d . [c.144]

Правила Хунда. Правила Хунда в приме 1ении к электронам данной электронной оболочки определяют характер заполнения электронами энергетических уровней и утверждают, что для основного состояния должны выполняться следующие требования [c.524]

В основе первого правила Хунда лежит принцип Паули и кулоновское отталкивание между электронами. Принцип Паулн не допускает, чтобы в одном и том же месте в данный момент времени оказались два электрона с одинаковыми направлениями спинов. Таким образом, электроны с одним и тем же направлением спина разделены в пространстве, и при этом разделены значительно по сравнению с электронами противоположных направлений спина. Вследствие кулоновского взаимодействия энергия электронов с одинаковыми направлениями спина понижается точнее говоря, средняя потенциальная энергия (будучи положительной) для параллельных спинов меньше, чем для антнпараллельных. [c.525]

Правила Хунда. Применять правила Хуида для нахождения основного состояния (с энергией, отвечающей основному уровню в обозначениях табл, 15.1) [c.539]

ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С МАГНИТНЫМ ПОЛЕМ ЛАРМОРОВСКИЙ ДИАМАГНЕТИЗМ ПРАВИЛА ХУНДА ПАРАМАГНЕТИЗМ ВАН ФЛЕКА ЗАКОН КЮРИ ДЛЯ СВОБОДНЫХ ИОНОВ ЗАКОН КЮРИ ДЛЯ ТВЕРДЫХ ТЕЛ АДИАБАТИЧЕСКОЕ РАЗМАГНИЧИВАНИЕ ПАРАМАГНЕТИЗМ ПАУЛИ ДИАМАГНЕТИЗМ ЭЛЕКТРОНОВ ПРОВОДИМОСТИ ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС. СДВИГ НАЙТА ДИАМАГНЕТИЗМ ЭЛЕКТРОНОВ В ЛЕГИРОВАННЫХ ПОЛУПРОВОДНИКАХ [c.259]

Такой результат связан с тем, что волновая функция основного состояния иона с заполненными оболочками сферически-симметрична. Указанное свойство является также одтшм из наиболее очевидных следствий правил Хунда (см. ниже). [c.263]

В одномерном случае доказано, что для основного состояния любого числа электронов с пе зависящим от спина взаимодействпем произвольного вида полный спин должен быть равен нулю [2]. Эта теорема не допускает обобщения на случай трех измерений, для которого, используя правила Хунда (см. гл. 31), можно найти множество примеров ее нарушения. [c.290]

Таким образом, совершенно не очевидно, какое основное состояние в приближении Хартри — Фока будет наилучшим. Кроме того (что еще хуже), простые попытки улучшить теорию Хартри — Фока приводят к радикальному изменению ее результатов. В настоящее время существует мнение, что газ свободных электронов, возможно, не является ферромагнитным ни при каких значениях плотности, хотя строгое доказательство этого отсутствует. Фактически ферромагнитные свойства обнаруживают только те металлы, отдельные ионы которых содержат частично заполненные д.- или /-оболочки, а такая ситуация безнадежно далека от области применимости модели свободных электронов. Чтобы объяснить магнитное упорядочение в металлах, необходимо рассматривать обменное взаимодействие между делокализованными электронами, учитывая при этом конкретные особенности зонной структуры ) и (или) особенности строения атомов, которые лежат в основе правил Хунда. [c.299]

См. такэке Восприимчивость Закон Кюри Правила Хунда Параметр Грюнайзена II 120—122, 136 в модели Дебая II 121 для щелочно-галоидных кристаллов II 122 См. также Тепловое расширение Параметр де Бура II 42, 43 Параметр порядка (в теории сверхпроводимости) II 362 аналогия с теорией ферромагнетизма II [c.403]

Необходимо сделать некоторые замечания о значениях J и g. В случае свободных магнитных нонов (парамагнитный газ) J можно определить, исходя из правил стабильности Хунда, а значение g получается из формулы Ланде [c.463]

Сильное взаимное влияние хим. связи и магн. взаимодействий обусловлено их противоположной тенденцией к коллективизации или локализации электронных состояний. Характерный пример — существование локализов. магн. моментов на ионах переходных металлов связано с наличием у ионов неспаренных электронов, к-рые в соответствии с правилами Хунда размещаются по энергетич. уровням так, что сниповой и орбитальный моменты ионов оказываются максимальными [1]. С др. стороны, хим. связывание атомов (в молекулах и твердых телах) состоит в образовании в большей или меньшей степени делокалияов. молекулярных орбиталей, к-рые заполняются в соответствии с принципом Паулн парами электронов с противоположными спинами (см. Паули, принцип). Это приводит, как правило, к компенсации магн. моментов отд. атомов. Обычно энергия хим. связи существенно превышает эиергию внутриатомных маги, взаимодействий. Поэтому атомы в большинстве органич. и но-органич. веществ не обладают локализов. магп. моментами, а сами вещества обнаруживают лишь диа-магн. свойства, присущие системам с заполненными электронными оболочками [2]. Однако атомы переход- [c.641]

ХУНДА ПРАВИЛО — правило дня нахождения самых глубоких уровнен энергии, соответствующих определённой электронной конфигурации атома при нормальной связи спиновых и орбитальных моментов образующих эти конфигурации электронов, когда уровни энергии характеризуются квантовыми числами 5, L (см. Атом, Атомные спектры). В случае нормальной связи моментов (см. Связь векторная) при заданном квантовом числе 5 полного спинового момента атома и при заданном квантовом числе полного орбитального момента атома L получается спектральный терм L с мультиплет-ностью K = 2.S-hl—совокупность уровней энергии с квантовыми числами J полного момента атома . / = L-bS, Z.-I-5— L —5 . Расположение мультиплетных термов L определяется электростатич. взаимодействиями электронов (много большими при нормальной связи, чем магн. взаимодействия) и, как следует из эксперим. данных и подтверждается мн. квантово.механич. расчётами, термы, соответствующие определённой конфигурации, лежат, как правило, тем глубже, чем больше 5, а при данном S имеют тенденцию лежать тем глубже, чем больше L. [c.417]

Согласно X. п., эмпирически установленному в 1925 Ф. Хундом (F. Hund), самый глубокий терм, соответствующий рассматриваемой электронной конфигурации, обладает наибольшим возможным значением S и наибольшим возможным для данного 5 значением L. Эго правило всегда выполняется для нормальных электронных конфигураций, соответствующих наиб, прочной связи всех электронов и состоящих из эквивалентных электронов, и полностью подтверждается квантовомеханич. расчётами. Напр., для конфигурации р получаются (при учёте Паули принципа) термы 5, D. Р, а для конфигурации [c.417]

ХУНДА ПРАВИЛО — эмпирич. способ определения взаимного расположения атомных уровней, соответствующих заданной электронной конфигу])ации, но обладающих различными значениями полного орбитального момента L и полного снина iS. С.огласно X. п., наименьшей энергией обладает состояние с наибольшим возможным нри даппой электроппой конфигурации значением S и наибольшим возмож- [c.383]

Смотреть страницы где упоминается термин Правило Хунда : [c.394] [c.630] [c.92] [c.168] [c.170] [c.419] [c.426] [c.432] [c.266] [c.283] [c.400] [c.370] [c.933] [c.293] [c.630] [c.634] [c.637] [c.328] [c.22] [c.384] Атомная физика (1989) — [ c.285 ]

Основы материаловедения и технологии полупроводников (2002) — [ c.22 ]

mash-xxl.info

Правило Хунда

Правило Хунда определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: модуль суммарного значения спинового квантового числа электронов данного подслоя должен быть максимальным. Сформулировано Фридрихом Хундом в 1925 году.

Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.

Другая формулировка: Ниже по энергии лежит тот атомный терм, для которого выполняются два условия.

1. Мультиплетность максимальна
2. При совпадении мультиплетностей суммарный орбитальный момент L максимален.

Разберём это правило на примере заполнения орбиталей p-подуровня p-элементов второго периода (то есть от бора до неона (в приведённой ниже схеме горизонтальными чёрточками обозначены орбитали, вертикальными стрелками — электроны, причём направление стрелки обозначает ориентацию спина):

Как видно, сначала появляется один электрон на 2p_x-орбитали, затем один электрон на 2p_y-орбитали, после этого один электрон на 2p_z-орбитали, затем появляются парные электроны на 2p_x-, 2p_y— и 2p_z-орбиталях.

Мнемоническое правило

Для запоминания Правила Хунда существует мнемоническое «правило трамвайного вагона»:

Ты приглядись, решив присесть,
К местам трамвайного вагона:
Когда ряды пустые есть,
Подсаживаться нет резона.

Wikimedia Foundation . 2010 .

Смотреть что такое «Правило Хунда» в других словарях:

правило Хунда — Hundo taisyklė statusas T sritis fizika atitikmenys: angl. Hund’s rule vok. Hundsche Regel, f rus. правило Хунда, n pranc. règle de Hund, f … Fizikos terminų žodynas

Правило Клечковского — (также Правило n+l; также используется название правило Маделунга) эмпирическое правило, описывающее энергетическое распределение орбиталей в многоэлектронных атомах. Правило Клечковского гласит: Заполнение электронами орбиталей в атоме… … Википедия

ХУНДА ПРАВИЛО — правило для нахождения самых глубоких уровней энергии, соответствующих определённой э л е к т р о н н о й к о н ф и г у р а ц и и атома при н о р м а л ь н о й с в я з и спиновых и орбитальных моментов образующих эти конфигурации электронов,… … Физическая энциклопедия

ХУНДА ПРАВИЛА — приближенные правила, определяющие относит. расположение энергетич. уровней атома. Получены Ф. Хундом в 1927 в результате анализа атомных спектров. Формулировка X. п. предполагает, что состояние многоэлектронного атома можно описать, указав т.… … Химическая энциклопедия

МАГНЕТИЗМ — 1) особая форма вз ствия между электрич. токами, между токами и магнитами (т. е. телами с магнитным моментом) и между магнитами; 2) раздел физики, изучающий это взаимодействие и св ва в в (магнетиков), в к рых оно проявляется. Основные проявления … Физическая энциклопедия

Мнемоника — Содержание 1 Основной метод запоминания в современной мнемонике 2 История … Википедия

Комплексные соединения — Цис платин одно из многих координационных соединений Комплексные соединения (лат. complexus сочетание, обхват) или координационные соединения (л … Википедия

Хунд, Фридрих — Фридрих Хунд нем. Friedrich Hund … Википедия

КРИСТАЛЛИЧЕСКОГО ПOЛЯ ТЕОРИЯ — квантовохим. теория, в к рой низшие по энергии состояния молекулы описываются как состояния одного атома (иона), находящегося в электростатич. поле, созданном остальными частицами. Как правило, К. п. т. применяется к координац. соед., кристаллам… … Химическая энциклопедия

P-элементы (химические) — p элементами называют химические элементы, в атомах которых электрон с наивысшей энергией занимает p орбиталь. p элементами являются: в 1 м периоде нет p элементов во 2 м периоде B Ne в 3 м периоде Al Ar в 4 м периоде Ga Kr в 5 м периоде In Xe в… … Википедия

dic.academic.ru

ПРАВИЛО ХУНДА;

КВАНТОВЫЕ ЧИСЛА. ПРИНЦИП ПАУЛИ. ПРИНЦИП НАИМЕНЬШЕЙ ЭНЕРГИИ. ЭЛЕКТРОННЫЕ ФОРМУЛЫ.

2.1. Квантовые числа и принципПаули

Для характеристики состояния электрона в атоме квантовая механика использует систему четырех квантовых чисел.

Главное квантовое число n – характеризует энергетический уровень, на котором находится электрон (общий запас его энергии), и принимает целочисленное значение натурального ряда чисел от 1 до∞,а для атомов элементов периодической таблицы в нормальном (невозбужденном) состоянии от 1 до 7 с увеличением n энергия электрона и размер орбитали возрастают.

Энергетическое состояние электронов одного уровня может несколько отличаться в зависимости от конфигурации (формы) их электронных облаков, образуя энергетические подуровни. Каждый энергетический уровень, соответствующий данному значению главного квантового числа n, разбивается от 0 — (n-1) энергетических подуровней. Энергетический подуровень электрона (форма орбитали и электронного облака) характеризуется побочным(орбитальным) квантовымчислом l, которое принимает целочисленное значение от 0 до (n-1). Каждой форме орбитали соответствует определенная величина момента количества электрона (М). М=h/2π∙ 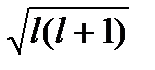), которая определяет энергию электрона. Например, если n=4, то l=0,1,2,3. Электроны, отвечающие этим значениям, называются соответственно s -, р -, d -, f-электронами, различающимися по форме; s-электроны – сфера ,

оси которых расположены по отношению друг к другу под углом 90°, и 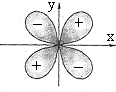обозначаются р_x р_y, p_z; d-электроны –четырехлепестковые, минимальное число d-орбиталей равно 5. Две d-орбитали, ориентированные по осям координат, обозначаются d_x 2 — d_у 2 , d_y 2 и d_z 2 ,

а три орбитали ориентированы между осями координат d_xy, d_xz, d_yz.

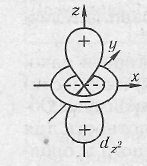
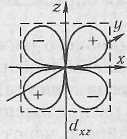
Расположение плоскости электронной орбитали, т.е. ее наклон относительно магнитной оси атома, ориентацию орбиталей в пространстве относительно направления внешнего магнитного поля характеризует магнитное квантовое число «m_l» связано с различными дозволенными углами поворота орбиталей в магнитном поле. Магнитное квантовое число принимает целочисленные значения от (-l) через 0 до (+l), т.е. на данном подуровне число ориентации равно (2l+1).

На s — подуровне одна ориентация, на р — подуровне три ориентации.

Электрон вращается также вокруг собственной оси в двух взаимно противоположных направлениях, что описывается спиновым квантовым числом m_s. Возникающие при этом собственные магнитные моменты электрона имеют два значения +1/2 и -1/2 в зависимости от того, совпадают они с ориентацией орбитального момента электрона или направлены в противоположную сторону.

Состояние электрона в атоме, отвечающее определенным значениям квантовых чисел n, l и m_l, называется атомной электронной орбиталью (АО). АО — область пространства, в которой пребывание электрона наиболее вероятно и электронное облако отличается наибольшей плотностью. Графически АО обозначается .

Согласно принципу Паули (ПП) в атоме не может быть двух электронов, характеризующихся одинаковым набором квантовых чисел, отсюда каждая АО может быть занята не более чем двумя электронами, различающимися спиновыми квантовыми числами 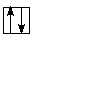– 1 — е следствие (ПП); 2-е следствие (ПП) – число атомных орбиталей на подуровне (2l + 1); 3-е следствие (ПП) число АО на уровне равно n 2 ; 4-е следствие (III) – максимальное число электронов на подуровне равно 2(2l + 1); 5-е следствие (III) – максимальное число электронов на уровне, равное – 2n 2 . Например, на 4-м энергетическом уровне максимальное число электронов равно 32 = (2·4 2 ).

Запрет Паули – максимальное число электронов на последнем энергетическом уровне равно восьми; меньше возможно, а больше восьми запрещается.

2.2. Распределение электронов в многоэлектронном атоме Принцип наименьшей энергии (правила Клечковского)

Для решения вопроса о распределении электронов в атоме, кроме обязательного учета принципа Паули, необходимо обязательно придерживаться принципа наименьшей энергии, формулировка его такова: в нормальном состоянии атома каждый электрон занимает то состояние из всех возможных, в котором он обладает наименьшей энергией (следовательно, наиболее прочной связью с ядром). Поэтому электрону необязательно занимать вышележащий энергетический уровень, если в нижележащем уровне есть места, располагаясь на которых электрон будет обладать меньшей энергией. Так как энергия электрона определяется значениями суммы главного (n) и орбитального (l) квантовых чисел (n + l), то АО заполняются в порядке последовательного возрастания их энергий и определяются двумя правилами Клечковского. Согласно этим правилам АО орбитали заполняются электронами в порядке последовательного увеличения суммы (n + l) (от меньшей суммы к большей) — (1-е правило Клечковского), а при одинаковых значениях суммы (n + l) у нескольких периодов заполнение подуровней происходит от меньшего значения n к большему значению l (2-e правило Клечковского).

Последовательность заполнения электронами энергетических уровней и подуровней в порядке возрастания их энергий имеет вид 1s 2 , 2s 2 , 2p 6 , 3s 2 , Зр 6 , 4s 2 , 3d 10 , 4p 6 ,5s 2 ,4d 10 , 5p 5 .

studopedia.su

ХУНДА ПРАВИЛО

— правило для нахождения самых глубоких уровней энергии, соответствующих определённой э л е к т р о н н о й к о н ф и г у р а ц и и атома при н о р м а л ь-н о й с в я з и спиновых и орбитальных моментов образующих эти конфигурации электронов, когда уровни энергии характеризуются квантовыми числами S, L (см. Атом, Атомные спектры). В случае нормальной связи моментов (см. Связь векторная )при заданном квантовом числе S полного спинового момента атома и при заданном квантовом числе полного орбитального момента атома L получается с п е к т р а л ь н ы й т е р м 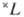с мультиплет-ностью 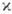=2S+1-совокупность уровней энергии с квантовыми числами J полного момента атома: J=L + S, L + S-1, . , |L — S|. Расположение мультиплетных термов 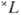определяется электростатич. взаимодействиями электронов (много большими при нормальной связи, чем магн. взаимодействия) и, как следует из эксперим. данных и подтверждается мн. квантовомеханич. расчётами, термы, соответствующие определённой конфигурации, лежат, как правило, тем глубже, чем больше S, а при данном S имеют тенденцию лежать тем глубже, чем больше L.

Согласно X. п., эмпирически установленному в 1925 Ф. Хундом (F. Hund), самый глубокий терм, соответствующий рассматриваемой электронной конфигурации, обладает наибольшим возможным значением S и наибольшим возможным для данного S значением L. Это правило всегда выполняется для н о р м а л ь н ы х э л е к т р о н н ы х к о н ф и г у р а ц и й, соответствующих наиб. прочной связи всех электронов и состоящих из эквивалентных электронов, и полностью подтверждается квантовомеханич. расчётами. Напр., для конфигурации р 2 получаются (при учёте Паули принципа )термы 1 S, 1 D, 3 Р, а для конфигурации d 2 — термы 1 S, 1 D, 1 G, 3 P, 3 F; в первом случае самый глубокий терм, согласно X. п., 3 Р, во втором — 3 F.

Для данного терма 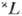уровни с различными J обладают разл. энергией-имеет место м у л ь т и п л е т н о е р а сщ е п л е н и е терма (при S L на 2L+1 составляющих), обусловленное магн. спин-орбитальным взаимодействием. Расположение уровней определяется приближённым п р а в и л о м и н т е р в ал о в, согласно к-рому расстояние между соседними уровнями с квантовыми числами J и J+1 пропорционально бoльшему квантовому числу; напр., для уровней 3 Р₀, 3 P₁, 3 Р₂. терма 3 Р расстояние 3 Р₂ — 3 Р₁ вдвое больше расстояния 3 Р₁ — 3 Р₀. При этом в случае конфигураций, состоящих из эквивалентных электронов, для оболочек, заполненных меньше чем наполовину (напр., р 2 , d 4 , f 5 ), получаются н о р м а л ь н ы е мультиплетные термы, для к-рых уровни лежат тем глубже, чем меньше J, а для оболочек, заполненных больше чем наполовину, получаются о б р ащ ё н н ы е мультиплетные термы, для к-рых уровни лежат тем глубже, чем больше J. Так, для нормального терма 3 Р конфигурации р 2 самый глубокий уровень 3 Р₀, а для обращённого терма дополнит. конфигурации р 4 — 3 Р₂.

X. п. в сочетании с правилом нахождения наиб. глубокого уровня энергии для нормальных и обращённых мультиплетных термов (это правило иногда ошибочно наз. вторым X. п.) позволяет определить для нормальной конфигурации атома самый глубокий (основной) уровень энергии в тех случаях, когда в атоме частично заполнена наиб. слабо связанными электронами одна оболочка типа пр 6 , nd 10 или nf 14 (при наличии в атоме лишь полностью укомплектованных электронных оболочек осн. уровнем атома является уровень 1 S₀, а при наличии одного внеш. электрона ns — уровень 2 S_l/2). Ниже приведены самые глубокие уровни энергии 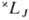для конфигурации эквивалентных электронов:

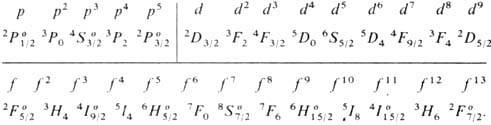
Отметим, что особенно глубоко (по сравнению с уровнями меньшей мультиплетности) лежат уровни 4 S_3/2, 6 S_5/2 и 8 S_7/2 для оболочек p 6 , d 10 и f 14 , заполненных как раз наполовину, т. е. для конфигураций р 3 , d 5 и f 7 .

Лит.:Hund F., Linienspektren und periodisches System der Eie-mente, В., 1927; Ландау Л. Д., Лифшиц Е. М., Квантовая механика. Нерелятивистская теория, 4 изд., М., 1989; Ельяшевич М. А., Спектры редких земель, М., 1953; его же, Атомная и молекулярная спектроскопия, М., 1962; Собельман И. И., Введение в теорию атомных спектров, 2 изд., М., 1977. М. А. Ельяшевич.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Последовательность заполнения электронных оболочек атомов

Два принципа определяют строение электронной оболочки атома элемента:

принцип Паули, который гласит: в атоме может существовать только один электрон с определенным набором квантовых чисел, что учитывает квантовые свойства возможных состояний атома;

принципом минимума энергии: при известном суммарном количестве электронов в атоме реализуется состояние с наименьшей энергией. Данный принцип является естественным для существования устойчивого состояния атома. Так как, если состояние атома не является состоянием с наименьшей энергией, то атом может под воздействием внутренних причин перейти в состояние с минимумом энергии.

Анализируя строение атома в первом приближении, пренебрегают энергией взаимодействия электронов. При этом энергию атома приравнивают к суммарной энергии электронов в поле, которое создается ядром атома. Отталкиваясь от данной известной энергии, находят распределение электронов по разным состояниям при учете принципа Паули и минимума энергии. При этом получают идеальную схему заполнения оболочек. Надо отметить, что идеальная схема заполнения может сильно отличаться от реально существующей. Исходя из принципа Паули, максимальное количество электронов (N), которое может находиться в оболочке равно:

где $n$ — главное квантовое число, $l=0,1. n-1$ (при заданном $n$) — орбитальное квантовое число.

Энергия электрона в поле ядра растет при увеличении главного квантового числа. Минимальную энергию имеют электроны на $K$ — оболочке ($n=1$), потом на $L$- оболочке ($n=2$) и далее. Что означает последовательное заполнение оболочек, начиная с $K \ (K,L,M. ).$

Надо заметить, что в первом приближении энергия электронов не зависит от орбитального квантового числа, поэтому для того, чтобы объяснить схему заполнения состояний $s,p,d,f. $ требуется учитывать взаимодействие между электронами. При этом получают, что их энергия взаимодействия растет с ростом $l$ (при заданном $n$). В идеальной схеме заполнения оболочки считают, что каждый новый присоединяющийся электрон связывается в состоянии с минимальными квантовыми числами $n,l$, которые допускает принцип Паули.

Правило Хунда определяет последовательность заполнения состояний электронов в рамках подгруппы, то есть при одном $l.$ Это правило гласит:

прежде всего, заполняются состояния имеющие разные величины магнитного квантового числа $m$ $(m=-l,-l+1,\dots l-1,l)$, при неизменном значении проекции спина; после того, как все $2l+1$ состояние по магнитному квантовому числу заполнены электронами начинается заполнение электронами, которые имеют противоположную ориентацию спина.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Так, в $p$-состояние ($l=1$) может находиться всего:

При этом состояния заполняются как:

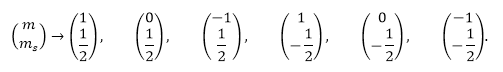
Другими словами правило Хунда можно сформулировать так:

в большинстве случаев электроны в атоме являются неспаренными, по возможности они имеют параллельные спины.

минимальной энергией обладает терм с наибольшим, из возможных при заданной конфигурации электронов величиной полного спина $(S)$. В том случае, если $S$ задано, то максимальным полным орбитальным моментом $(L)$.

Явление ферромагнетизма железа, кобальта, никеля объясняют как результат следствия правила Хунда. $3d$ — подоболочки данных элементов имеют частичное заполнение, при этом электроны в подоболочках являются неспаренными. В такой ситуации спиновые магнитные моменты не компенсируются. В $Fe$ из шести $3d$ — электронов пять обладают параллельными спинами. В результате каждый атом железа имеет большой суммарный магнитный момент.

Правило Хунда вызвано тем, что электроны в атоме взаимно отталкиваются. В результате энергия атома уменьшается с увеличением расстояния между электронами. Электроны, которые находятся в одной подоболочке и имеют одинаковые направления спинов, имеют разные величины магнитного квантового числа и, следовательно, определяются волновыми функциями с отличными распределениями в пространстве. Получается, что электроны, обладающие параллельными спинами, отстоят в пространстве дальше друг от друга, чем спаренные электроны. Такая конфигурация имеет меньшую энергию и значит, является более устойчивой.

Следствие правила Хунда

Только те атомы могут образовать молекулы, у которых присутствует один или более неспаренных электронных спинов. По правилу Хунда в одной подоболочке электроны имеют столько параллельных спинов, сколько это возможно (то есть направление спина одинаково у максимального числа электронов). При этом все атомы (исключая атомы с замкнутыми подоболочками) обладают неспаренными электронами, следовательно, могут создавать связи (вступать в реакции). Из сказанного выше можно сделать вывод о том, что все элементы с незамкнутыми внешними оболочками могут создавать химические соединения.

Правила Хунда (используются для построения основного терма):

• ниже по энергии расположен терм, мультиплетность которого максимальна;
• если мультиплетности равны, то минимальна энергия у терма, которому принадлежит максимальная величина суммы орбитального момента.

Лень читать?

Задай вопрос специалистам и получи
ответ уже через 15 минут!

spravochnick.ru