Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Законы Вольта

Согласно закону Вольта в замкнутой цепи из нескольких разнородных термоэлектродов с одинаковой температурой во всех переходных спаях термоток, не возникает. В соответствии с этим из рассмотрения цепей из двух А, В) и из трех (Л, В, С) термоэлектродов можно получить [c.174]

Первый закон Вольта при соединении между собой двух проводников между ними возникает контактная разность потенциалов, зависящая от вида вещества и температуры места контакта [c.214]

Второй закон Вольта разность потенциалов между крайними участками цепи, состоящей из последовательно соединенных проводников с одинаковой температурой, не зависит от вида промежуточных проводников и равна разности потенциалов, возникающей при непосредственном контакте крайних веществ. [c.214]

Фурье 226 Законы Вольта 235 [c.512]

На основании закона Вольта в замкнутой цепи, состоящей из двух разнородных проводников А я В, когда температуры мест их соединения одинаковы (4 = О и отсутствуют посторонние э. д. с., термотока не возникает. Вследствие этого необходимо принять, что возникающие при этом контактные термо-э. д. с. в местах соединения / и 2 равны между собой, но различны по знаку, и поэтому суммарная термо-э. д. с. Е цепи равна нулю [c.88]

Закон Вольта можно распространить также и на замкнутую цепь, состоящую из любого числа различных однородных проводников А, В, С,. . М, N. Тогда при одинаковой температуре t мест их соединения сумма контактных термо-э. д. с. равна нулю [c.89]

Если известны термо-э. д. с. различных термоэлектродных материалов В, С, О,. . N в паре с платиновым термоэлектродом А, то на основании закона Вольта можно определить термо-э. д. с. любой комбинации этих термоэлектродов между собой для опре- [c.96]

По закону Вольта в замкнутой цепи, образованной из любого числа разнородных проводников, не может быть получен ток, если температуры мест соединения этих проводников одинаковы. [c.88]

С помощью метода Томаса — Ферми можно вычислить полную энергию ионизации атома, т. г. энергию, необходимую для удаления всех электронов из нейтрального атома, путем вычисления электростатической энергии распределения для плотности зарядов в атоме. Искомая полная энергия будет равна половине этой электростатической энергии, так как для системы частиц, взаимодействующих по закону Кулона, средняя кинетическая энергия равна средней потенциальной энергии, взятой с отрицательным знаком. Расчет дает, что полная энергия ионизации —W , выраженная в электрон-вольтах, равна [c.210]

Для законов распределения формул (9) и (10) примем Ь = 0,5 (вольты), 00,2 = 0,288 (вольты), = 0,005 (радианы), Оо,4 = 0,004 1/сек) и предположим, что точность измерительных средств, применяющихся при контроле рассмотренных параметров системы, составляет 14% от их наибольших значений, оговоренных техническими требованиями. Пользуясь формулой (12), построим композицию законов распределения случайных величин и 63. Теперь с учетом изложенного преобразуем законы распределения случайных величин по следующим схемам [2] [c.39]

Падение напряжения в ошиновке рассчитывают по отдельным элементам ошиновки и прибавляют падение напряжения в контактах. На тех элементах ошиновки, в которых сила тока не изменяется по длине, падение напряжения может быть вычислено (в вольтах) по закону Ома [c.290]

Электрическое сопротивление. Единица сопротивления ом (Ом) — сопротивление проводника, в котором протекает ток один ампер при разности потенциалов на его концах один вольт. Закон Ома определяет размерность (см. (7.92)) [c.220]

Понятие об электрическом токе. Проводники и изоляторы электрического тока. Напряжение. Единицы измерения напряжения — вольт. Сила тока. Единица измерения силы тока — ампер. Сопротивление. Единица измерения сопротивления — ом. Закон Ома. [c.551]

Для газонаполненных фотоэлементов отступления от закона Столетова имеют место даже при малых освещенностях. Их вольт-амперные характеристики таковы, что достигнуть состояния насыщения фототока невозможно ни нри каких условиях. Они обладают значительной инерционностью и т. д., так что для фотометрических целей пользоваться ими не рекомендуется. [c.305]

Происхождение несмещенной компоненты в спектре рассеянного излучения обусловлено внутренними электронами атомов мишени. Ил энергия связи, особенно в тяжелых атомах, сравнима с энергией рентгеновских фотонов, и, следовательно, такие электроны уже нельзя рассматривать как свободные. Поэтому в акте рассеяния фотон обменивается энергией и импульсом с атомом в целом, а так как масса атома велика, то по закону сохранения импульса фотон практически не передает ему своей энергии. Фотоны, рассеянные внутренними электронами, образуют несмещенную компоненту. Из приведенных рассуждений ясно, почему эффект Комптона нельзя наблюдать в видимой области спектра. Энергия фотона видимого света составляет лишь несколько электрон-вольт. При этом даже внешние электроны нельзя считать свободными. [c.470]

Вольт-амперная характеристика воздушного промежутка с однородным электрическим полем представлена на рис. 2-3. На участке 1 кривой при низких значениях приложенного напряжения выполняется закон Ома плотность тока равна [c.67]

При изменении напряжения с на — / ток в полупроводнике потечет в обратном направлении и будет изменяться по такому же закону (рис. 54) это значит, что полупроводник имеет симметричную вольт-амперную характеристику. [c.93]

При приложении к слою газа электрического напряжения в нем возникает ток проводимости (рис. 9). С дальнейшим повышением напряжения наступает пробой газа (точка П на рис. 9). Пробой в однородном электрическом поле происходит в виде искрового разряда (искры), соединяющего металлические электроды, поме- Рис. 9. Зависимость тока от щенные в газовой среде. Явление напряжения (вольт-амперная пробоя газообразных диэлектриков характеристика) для воздуха в однородном электрическом поле описывается законом Пашена, согласно которому пробивное напряжение ( /пр) всякого газообразного диэлектрика (газа) есть функция произведения давления газа (р) на толщину (Л) слоя газа [c.15]

Р (в ваттах) = V (напряжение в вольтах) X I (сила тока в амперах). Но напряжение по закону Ома может быть представлено в виде произведения силы тока на сопротивление г. [c.10]

Для газового разряда сопротивление не является постоянным (R ф onst), так как число заряженных частиц в нем зависит от интенсивности ионизации и, в частности, от тока. Поэтому электрический ток в газах не подчиняется закону Ома и вольтам-перная характеристика разряда для газов является обычно нелинейной. [c.38]

Выше мы рассматривали спонтанное и вынужденное деление ядер на две части как наиболее вероятное деление. При оценке некоторых количественных соотношений (VIИ.4) для простоты расчетов мы принимали деление симметричным (fe = /а)- В действительности при спонтанном делении, а также при делении, вызванном тепловыми нейтронами и нейтронами с энергией в несколько мегаэлектрон-вольт, обычно образуются асимметричные осколки с массами в отношении 3 2. Неодинаковой оказывается и энергия осколков более легкий осколок приобретает большую энергию. Обозначим через Su Смотреть страницы где упоминается термин Законы Вольта : [c.239] [c.57] [c.108] [c.111] [c.278] [c.131] [c.310] [c.312] [c.467] [c.49] [c.256] [c.105] Теплоэнергетика и теплотехника Общие вопросы Книга1 (2000) — [ c.235 ]

mash-xxl.info

Контактная разность потенциалов

Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разностью потенциалов. Итальянский физик А. Вольта (1745—1827) установил, что если металлы А1, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта. Контактная разность потенциалов для различных металлов составляет от десятых до целых вольт.

1. Контактная разность потенциалов зависит лишь от химического состава и температуры соприкасающихся металлов.

Для объяснения возникновения контактной разности потенциалов воспользуемся представлениями зонной теории. Рассмотрим контакт двух металлов с различными работами выхода А1 и А2, т.е. с различными положениями уровня Ферми (верхнего заполненного электронами энергетического уровня). Если A1

Так как для соприкасающихся металлов уровни Ферми совпадают, а работы выхода А1 и A2 не изменяются (они являются константами металлов и не зависят от того, находятся металлы в контакте или нет), то потенциальная энергия электронов в точках, лежащих вне металлов в непосредственной близости к их по­верхности (точки А и В на рис. 1, б), будет различной. Следовательно, между точками А и В устанавливается разность потенциалов, которая, как следует из рисунка, равна

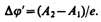(1.1)

Разность потенциалов, обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов. Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.

Если уровни Ферми для двух контактирующих металлов не одинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенциалов, которая, как следует из рисунка, равна

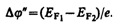(1.2)

В квантовой теории доказывается, что причиной возникновения внутренней контактной разности потенциалов является различие концентраций электронов в контактирующих металлах

Если, например, привести в соприкосновение три разнородных проводника, имеющих одинаковую температуру, то разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах. Онане зависит от природы промежуточных проводников (второй закон Вольта).

Внутренняя контактная разность потенциалов возникает в двойном электрическом слое, образующемся в приконтактной области и называемом контактным слоем. Толщина контактного слоя в металлах составляет примерно 10^-10 м, т. е. соизмерима с междоузельными расстояниями в решетке металла. Число электронов, участвующих в диффузии через контактный спой, составляет примерно 2% от общего числа электронов, находящихся на поверхности металла. Столь незначительное изменение концентрации электронов в контактном слое, с одной стороны, и малая по сравнению с длиной свободного пробега электрона его толщина — с другой,

не могут привести к заметному изменению проводимости контактного слоя по сравнению с остальной частью металла. Следовательно, электрический ток через контакт двух металлов проходит так же легко, как и через сами металлы, т.е. контактный слой проводит электрический ток в обоих направленияходинаково и не дает эффекта выпрямления, который всегда связан с односторонней проводимостью.

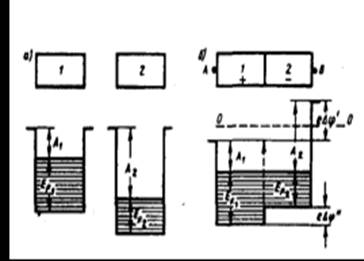рис. 1

3. Термоэлектрические явления

Термоэлектрические явления объединяют группу физических процессов, обусловленных взаимными превращениями энергии теплового движения и энергии электрического тока. К ним относят обычно три эффекта — Зеебека, Пельтье и Томсона.

Эффект Зеебека (1821 г.) заключается в том, что в электрической цепи, состоящей из последовательно соединенных элементов, изготовленных из различных материалов, возникает электрический ток, если места контактов поддерживаются при неодинаковых температурах. При разрыве одного из проводников на концах цепи возникает разность потенциалов — термоэлектродвижущая сила (термоЭДС, ТЭДС). Электрическая цепь, в которой возникает термоЭДС, называется термоэлектрической цепью, а материалы, из которых составлена термоэлектрическая цепь, — термоэлектродами. Пара разнородныхтермоэлектродов, гальванически соединенных на одном конце (в виде рабочего спая), образуют термопару — чувствительный элемент термоэлектрического преобразователя. Обычно в метрологической практике оценку термоЭДС конкретного материала проводят по отношению к термоэлектроду из чистой платины (нормальному платиновому термоэлектроду).

Сегодняшних знаний о причинах и механизме возникновения термоЭДС недостаточно для ее точного вычисления. Отсутствие общепризнанной теории возникновения термоЭДС обусловлено чрезвычайной сложностью механизмов процесса. ТермоЭДС реального металла зависит от распределения электронов по скоростям (энергиям), связанного с температурой и энергией Ферми, строения решетки металла, интенсивности ее колебаний, механизмов рассеяния носителей тока на реальной решетке, примесных атомах, фононах и между собой. Сложность связей приводит к тому, что коэффициенты термоЭДС различных металлов и сплавов значительно отличаются друг от друга и от теоретически предсказанных значений.

Эффект Пельтье (1834 г.) состоит в том, что при прохождении тока в цепи с проводниками из разнородных материалов в местах контактов помимо выделения джоулевой теплоты поглощается или выделяется (в зависимости от направления тока и типа вещества) некоторое количество теплоты:

где П — коэффициент Пельтье; I — сила тока; τ — время.

Эффект Пельтье проявляется именно в спаетармопары, что позволяет использовать его для таких практических задач, как контроль качества рабочего спая и диагностика качества заделки рабочего спая натермометрируемом объекте.

Эффект Томсона (1856 г.) заключается в том, что в зависимости от направления тока при его прохождении по однородному проводнику, вдоль которого имеется градиент температуры (т.е. при наличии в цепи одновременно и электрического тока, и потока теплоты), в объеме однородного проводника выделяется или поглощается теплота. Эта теплота выделяется (поглощается) в дополнение к выделяющейся теплоте Джоуля — Ленца (резистивный нагрев).

Количество теплоты Томсона Qσ пропорционально силе тока I и градиенту температуры ∆T:

где σ – коэффициент Томсона, В/К-1, τ — время, с.

В замкнутой цепи, по которой протекает ток, при наличии градиента

температуры возникают все три термоэлектрических явления, связанных между собой соотношениями Кельвина, позволяющими определять величину любого из трех эффектов, если известна величина хотя бы одного из них.

На эффекте Зеебека основано измерение температуры с помощью термоэлектрических преобразователей (термопар): величина термоЭДС оказывается пропорциональной разности функций температур спаев термоэлектрической цепи. При незначительных разностях температур спаев можно принять, что развиваемая термоЭДС пропорциональна ∆Т. То есть, если точки спаев двух проводников термоэлектрической цепи помещены в среды с разными температурами (рис.2), то

или в дифференциальной форме

где ∆Е — термоЭДС, a -дифференциальная или удельная термоЭДС данной пары металлов. Измеряется она в В/К и существенно зависит от природы контактирующих материалов, а также интервала температур, достигая порядка 10^-5 ÷10^-4 В/К. В небольшом интервале температур (0-100°С) удельная термоЭДСслабо зависит от температуры

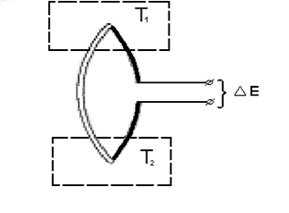рис. 2Схема термоэлектрической цепи.

Из (2.1) следует, что a численно равен величине термоЭДС, возникающей в цепи при разности температур спаев, равной одному градусу. Термоэлектрический коэффициент а обычно измеряется в вольтах (милливольтах) на градус. В общем случае величина a является функцией температуры.

Если принять для упрощения, что a ≠f(T), то, интегрируя уравнение (2.2), получим

где индексы 1 и 2 относятся соответственно к горячему и холодному спаям термоэлектрической цепи (условимся называть горячим тот спай цепи, который находится при более высокой температуре; другой спай будем именовать холодным, т.е. Т2>Т1).

Понятно, что если замкнуть эту цепь через какое-либо внешнее электрическое сопротивление (обмотка электродвигателя, электронагреватель и т. д.), то в термоэлектрической цепи возникает ток (рис. 3).

Если изменить температуры спаев на обратные (т. е. спай, находя-щийся при

температуре Т1, поместить в среду с температурой Т2, а другой спай, температура которого была равна Т2, поместить в среду с температурой Т1), то в цепи возникает ток, равный по величине току при прежних температурах спаев, но текущий в противоположном направлении.

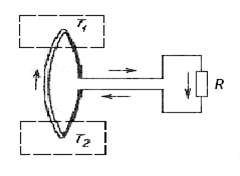Рис. 3. Схема термоэлектрического генератора.

Из изложенного следует, что термоэлектрический эффект, в принципе, может быть использован для целей производства электроэнергии. Впервые вопрос о создании термоэлектрического генератора, основанного на использовании эффекта Зеебека, был поставлен еще в 1885 г. английским физиком Рэлеем. Однако долгое время эта идея не была реализована вследствие того, что известные в то время термоэлектродные материалы позволяли соорудить термоэлектрические генераторы лишь с очень малыми значениями термоэлектрического КПД. И хотя впоследствии были созданы перспективные полупроводниковые термоэлектрические генераторы, значительно более широкое использование получил эффект Зеебека в измерительной технике при измерении температур термоэлектрическими преобразователями.

Измерив величину термоЭДС Е1-Е2 и зная температуру одного из спаев термопары, можно определить температуру среды, в которую помещен другой (рабочий) спай. Разумеется, для этого надо знать значение коэффициента a, которое определяется предварительной тарировкой (градуировкой).

В современной термометрии термоэлектрические термометры занимают наибольший удельный вес, составляя около 55 % от общего числа контактных термометров, применяющихся на промышленных предприятиях и в научных учреждениях.

термоЭДС термопары обусловлена тремя причинами. Первая заключается в зависимости уровня Ферми энергии электронов в проводнике от

температуры, что приводит к неодинаковым скачкам потенциала при переходе из одного металла в другой в спаях термопары, находящихся при разных температурах. Во-вторых, при наличии градиента температуры электроны в области горячего конца проводника приобретают более высокие энергии и подвижность. Вдоль проводника возникает градиент концентрации электронов с повышенными значениями энергии, что влечет за собой диффузию более быстрых электронов к холодному концу, а более медленных — к горячему. Но диффузионный поток более быстрых электронов оказывается больше. В-третьих, при наличии градиента температуры вдоль проводника возникает дрейф фононов — квантов энергии колебаний кристаллической решетки. Сталкиваясь с электронами, фононы сообщают им направленное движение от более нагретого конца проводника к более холодному. Последние два процесса приводят к избытку электронов вблизи холодного конца и недостатку их вблизи горячего конца. В результате внутри проводника возникает электрическое поле, направленное навстречу градиенту температуры. Таким образом, термоЭДС термопары возникает только из-за наличия продольного градиента температуры в проводниках, составляющих термопару.

Термоэлектродвижущая сила, развивающаяся на концах однородного проводника (ТЭДС Томсона), зависит от его природы, а ее величина для конкретного проводника А определяется соотношением

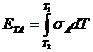(2.4)

где σА- коэффициент Томсона для проводника А; Т2>Т1.

Если из одного однородного проводника А составить замкнутую цепь (рис.4 а) и поддерживать в ее крайних точках температуры Т1 и Т2, то вследствие кругового движения за-рядов по замкнутой цепи направление движения их в одной половине цепи будет совпадать с положительным направлением градиента температуры, а в другой — с отрицательным. Поэтому в обеих ветвях цепи возникают ТЭДС Томсона, равные по величине и противоположные по знаку, которые во всей замкнутой цепи взаимно компенсируются. Таким образом, в замкнутой цепи, состоящей из одного однородного проводника, ТЭДС Томсона равна нулю при любом

распределении температуры вдоль проводника. Если же замкнутая цепь состоит из двух различных однородных проводников А и В (рис. 4 б), то суммарная ТЭДС Томсона в цепи

равна разности ТЭДС, возникающих в каждой ветви, и определяется по

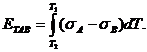(2.5)

То есть в замкнутой цепи, состоящей из пары проводников А и В, суммарная ТЭДС зависит от температур Т1 и Т2 в местах их соединения

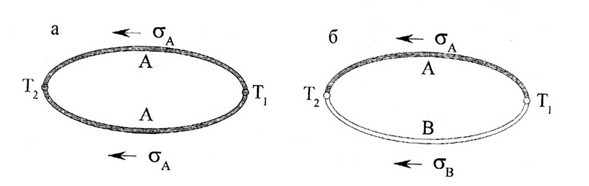
Рис. 4. Распределение потенциалов в цепи идеальной (с однородными по всей длине термоэлектродами) термопары: а — замкнутая цепь из одного однородного проводника А; б — замкнутая цепь из пары однородных проводников А и В.

mydocx.ru

Контактная разность потенциалов закон вольта

Как показывает опыт, на контакте двух различных металлов образуется двойной электрический слой и соответствующая разность потенциалов (рис. 6.8).

Появление двойного электрического слоя обусловлено различием работ выхода электронов из металлов. Чем она больше, тем меньше вероятность перехода электронами границы раздела. Поэтому со стороны металла с большей работой выхода накапливается отрицательный заряд, а с противоположной – положительный.

Это явление наблюдалось итальянским физиком Александро Вольта (1745 – 1827), который сформулировал два экспериментальных закона, известных как законы Вольта.

1. На контакте двух разных металлов возникает разность потенциалов, которая зависит от химической природы и от температуры спаев.

2. Разность потенциалов на концах последовательно соединенных проводников не зависит от промежуточных проводников и равна разности потенциалов, возникающей при соединении крайних проводников при той же температуре.

Результаты эксперимента можно объяснить с позиции классической электронной теории. Если принять, что потенциал за пределами металла равен нулю, то энергия электрона внутри металла с потенциалом φ_iопределится выражением

При соединении двух разных металлов (рис. 6.9)с работами выхода

и ,

возникает избыточный переход электронов из второго металла в первый, так как В результате концентрация электронов n₁ в металле 1 увеличивается, по сравнению с n₂, что порождает обратный избыточный поток электронного газа за счет диффузии, противоположный потоку, обусловленному разностью работ выхода.

Установившаяся разность потенциалов в равновесном состоянии определяется как:

,

где – разность потенциалов, обусловленная разными работами выхода электронов из металлов, а – разность потенциалов, возникающая на границе раздела за счет неодинаковой концентрации электронов в электронном газе.

Установившуюся разность потенциалов можно найти из выражения:

Явление возникновения контактной разности потенциалов и ее зависимость от температуры называют термоэлектрическим эффектом или эффектом Зеебека. Эффект Зеебека (прямой термоэлектрический эффект) заключается в появлении разности потенциалов в термопарах.

Схема термопары состоящей из спая двух разных металлов 1 и 2, показана на рисунке 6.10.

На концах термопары возникает термоЭДС термопары E :

ens.tpu.ru

Контактная разность потенциалов.

Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разность потенциалов. Итальянский физик А.Вольта(1745-1827) установил, что если металлы Al, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта. Контактная разность потенциалов для различных металлов составляет от нескольких десятых до целых вольт.

Вольта экспериментально установил два закона:

2. Контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.

Объяснение этих законов можно дать на основе классической электронной теории металлов. Приведем в соприкосновение два различных металла 1 и 2 с работами выхода A₁, и A₂, причем A₂ > A₁. Электроны, оказавшиеся у поверхности раздела металлов, совершая тепловое движение, легче переходят из металла, для которого работа выхода меньше, в металл, для которого работа выхода больше. В рассматриваемом случае электроны будут переходить из металла 1 (и он заряжается положительно) в металл 2 (заряжается отрицательно) до тех пор, пока работа по перемещению электрона за счет контактной разности потенциалов не станет равной разности работ выхода:

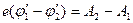
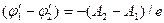. (1)

Различие в работах выхода — не един­ственная причина появления контактной разности потенциалов. Выражение (1) получено при условии, что концентра­ция свободных электронов в металлах одинакова. Предположим, что n₁ и п₂ — соответственно концентрации электронов в металлах 1 и 2, причем n₁> п₂. При этих условиях начнется преимущественный пе­ренос электронов из первого металла во второй, в результате чего первый металл зарядится положительно, а второй — отри­цательно. Между металлами возникнет разность потенциалов 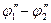, которая, согласно теоретическим расчетам, равна

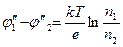(2)

Как правило, .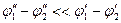

Обе причины возникновения контакт­ной разности потенциалов (различие в работах выхода и концентраций свобод­ных электронов) могут действовать как в одном и том же направлении, так и в противоположных (в разобранных нами случаях 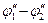имеет гот же знак, что и 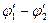). Контактная разность потен­циалов, обусловленная обеими причина­ми, согласно (1) и (2), равна

(3)

Уравнение (3) — математическое вы­ражение первого закона Вольта; оно по­казывает. что 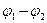зависит только от температуры и химическою состава со­прикасающихся проводников (Т, А₁, А₂, n₁, и n₂).

Для доказательства второю закона Вольта приведем в соприкосновение три разнородных проводника, имеющих оди­наковую температуру (рис. 1).

Рис.1

Разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах:

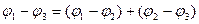
Пользуясь формулой (3), получим

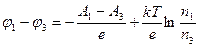
т. е. 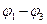действительно не зависит от природы промежуточных проводников.

Если из рассмотренных металлов со­ставить замкнутую цепь (рис. 1, пунк­тирная линия), то приложенная электро­движущая сила 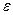равна алгебраической сумме всех скачков потенциалов, встречающихся при обходе замкнутой цепи:

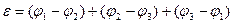
Используя формулу (3), получим

Таким образом, при образовании замкну­той цепи из нескольких металлических проводников с одинаковой температурой спаев невозможно возникновение электро­движущей силы за счет только контакт­ных скачков потенциала.

Дата добавления: 2015-08-29 ; просмотров: 469 . Нарушение авторских прав

studopedia.info