Из того, что было сказано в предыдущем параграфе, становится ясно, почему тело при условиях, показанных на рисунке 163, б, находится в равновесии.

Поступательно тело не может двигаться, потому что ось закреплена. Поворачиваться же оно не может потому, что моменты сил и равны друг другу по абсолютному значению, но одна сила может повернуть тело по часовой стрелке, а другая — против. И если приписать моментам сил, вращающим это тело в противоположных направлениях, разные знаки, то алгебраическая сумма этих двух моментов окажется равной нулю.

Тело, способное вращаться вокруг закрепленной оси, находится в равновесии, если сумма моментов сил относительно закрепленной оси, вращающих тело по часовой стрелке, равна сумме моментов сил относительно той же оси, вращающих его против часовой стрелки.

Это и есть правило моментов — условие равновесия тела, имеющего закрепленную ось вращения.

Момент силы зависит от двух величин: от значения самой силы и длины плеча. Один и тот же момент силы может быть создан малой силой, плечо которой велико, и большой силой с малым плечом. Если, например, пытаться закрыть дверь, толкая ее

поблизости от петель, то этому с успехом сможет противодействовать ребенок, который догадается толкать ее в другую сторону, приложив силу поближе к краю, и дверь останется в покое (рис. 164).

В справедливости правила моментов можно убедиться на опытах, которые проводятся с прибором, изображенным на рисунке 165. Он представляет собой диск А, укрепленный на оси, проходящей через его центр. На диске нанесены окружности, радиусы которых последовательно увеличиваются на 1 см, так что радиус первой, ближайшей к центру окружности равен 1 см, Второй — 2 см и т. д. На окружностях по нескольким диаметрам диска вбиты гвоздики, к которым можно привязывать нити с гирями. Нити переброшены через блоки В и С. Привязывая нити к гвоздикам на разных окружностях и подвешивая к ним различные грузы, создают различные моменты сил, действие которых можно уравновесить моментом силы тяжести третьего груза, подвешенного непосредственно к диску. При этом легко убедиться, что диск находится в равновесии, т. е. не поворачивается, когда алгебраическая сумма моментов всех трех сил равна нулю.

Величина момента силы, с которым действует каждый из грузов, определяется произведением силы тяжести груза на длину перпендикуляра, опущенного из центра диска на нить. Длина же этого перпендикуляра, выраженная в сантиметрах, равна номеру окружности, которой касается нить в точке, куда опущен перпендикуляр.

Нетрудно понять, что из правила моментов следует знаменитое правило рычага: рычаг находится в равновесии, когда действующие на него силы обратно пропорциональны плечам. Но это не что иное, как другое выражение правила моментов! Не следует думать, что к рычагу должны быть приложены обязательно параллельные силы. На рисунке 166 показан пример рычага, к которому приложены взаимно перпендикулярные силы

Теперь мы можем сформулировать общее условие равновесия тела:

Для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю геометрическая сумма приложенных к телу сил и сумма моментов этих сил относительно оси вращения.

Задача. Однородный стержень массой 2 кг прикреплен своим нижним концом к шарниру (рис. 167). К другому его концу подвешен груз массой 2 кг. Стержень удерживается в равновесии горизонтальной оттяжкой, прикрепленной к неподвижной вертикальной стойке. Пользуясь числами, указанными на рисунке, найдите силу натяжения оттяжки.

Решение. На стержень действуют четыре силы: сила тяжести, приложенная к его середине, сила тяжести груза сила упругости оттяжки и сила упругости в шарнире. Осью вращения служит шарнир у нижнего конца стержня. Из перечисленных сил только первые три создают вращающие моменты относительно этой оси. Линия действия силы реакции в шарнире проходит через ось шарнира, и ее момент равен нулю. Из трех указанных сил только одна сила упругости оттяжки поворачивает стержень против часовой стрелки. Две другие вращают его по часовой стрелке. По правилу моментов

Решая это уравнение, получаем:

1. На рисунке 168 изображен однородный стержень, ось вращения которого находится в точке О. На нем в точках А и В подвешены грузы массой

0,2 кг и 0,4 кг соответственно. Какой массы груз должен быть подвешен в точке С, чтобы стержень находился в равновесии?

2. К однородному стержню, который может вращаться вокруг оси О, прикреплен в точке А груз массой 0,8 кг (рис. 169). Какой массы груз нужно прикрепить в точке В, чтобы стержень был в равновесии, если масса стержня 400 г?

3. Приведите примеры практического использования рычага.

4. Покажите, что правило рычага следует из правила моментов.

5. При каком условии рычаг, показанный на рисунке 166, находится в равновесии?

lib.alnam.ru

Правило моментов

С тех пор как Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский ученый П. Вариньон придал ему более общую форму, воспользовавшись понятием момента силы.

Моментом силы называется физическая величина, равная произведению силы на ее плечо:

М — момент силы, F — сила, l — плечо силы.

Докажем, что рычаг находится в равновесии, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки, т. е.

Для доказательства этого равенства воспользуемся формулой (20.1). Используя свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), перепишем эту формулу в виде

Но F₂l₂ = M₂ — момент силы, стремящейся повернуть рычаг по часовой стрелке (см. рис. 50), а F₁l₁ = M₁ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, M₁ = M₂ , что и требовалось доказать.

Формула (21.2) выражает правило моментов. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси. Таково, например, тело, изображенное на рисунке 53. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой O . Плечом силы F₁ в данном случае является расстояние l₁ от оси вращения до линии действия силы. 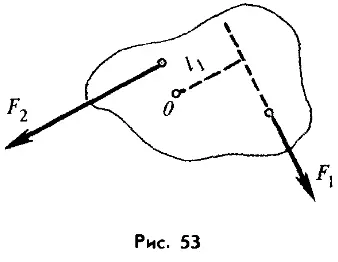В общем случае момент силы находят следующим образом. Сначала проводят линию действия силы. Затем из точки O , через которую проходит ось вращения, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы. Умножив силу на ее плечо, получают момент силы относительно оси вращения.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.

Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.

1. Что называют моментом силы? 2. Сформулируйте правило моментов. 3. Что характеризует момент силы? 4. Почему ручку у двери прикрепляют на противоположной от петель стороне? 5. Как находится момент силы в общем случае? 6. Что принимают за единицу момента силы?

phscs.ru

Момент силы правило момента

Важное замечание! Для просмотра анимации Ваш броузер должен поддерживать тип файла .SWF. Проверьте, и при необходимости установите программу FLASH PLAYER, загрузив ее с сайта www.macromedia.com .

Моменты сил.Правило моментов.

Из курса Физики нам известно, что вращающее действие силы характеризуется произведением модуля силы на расстояние от оси вращения до линии действия силы. Величина, равная этому произведению, носит название вращающий момент или момент силы. Обозначим момент силы F буквой M , расстояние от оси вращения до линии ее действия буквой d , тогда можно записать:

Величина d называется плечом силы. Моментам сил, вращающих тело по часовой стрелке, приписывают положительный знак, а против — отрицательный. Итак, правило моментов формулируется следующим образом: Тело, способное вращаться вокруг оси, находится в равновесии если алгебраическая сумма моментов приложенных сил относительно оси равна нулю. Это и есть условие равновесия тела, имеющего закрепленную ось вращения.

Из выражения для момента следует, что за единицу вращающего момента нужно принять момент силы в 1Н, линия действия которой отстоит от оси вращения на 1м. Эту единицу называют ньютон — метром(Нм).
Момент силы зависит от двух величин: от абсолютного значения силы и длины плеча. Один и тот же момент силы может быть создан малой силой, плечо которой велико, и большой силой с малым плечом.
Из правила моментов следует правило рычага: рычаг находится в равновесии, когда действующие на него силы обратно пропорциональны плечам.

Таким образом общее условие равновесия формулируется так: Для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю равнодействующая приложенных сил и сумма моментов этих сил относительно оси вращения (выполнение этих условий не мешает телу совершать равномерное прямолинейное движение или вращение с постоянной скоростью).

Попробуйте уравновесить рычаг (Рис.1.) разными способами.

Пример решения задачи.

Однородное бревно массой M=200 кг длиной L=6 м лежит на краю обрыва. Конец бревна выступает за край обрыва на b=2.5 м. На какое расстояние от края обрыва может отойти по выступающему концу человек массой m=80 кг.

Необходимыми условиями, определяющими равновесие тела, если у него нет закрепленной оси вращения, являются условия равенства нулю суммы сил и суммы моментов сил.

Бревно будет находиться в покое до тех пор, пока суммарный момент сил со стороны свешивающейся части бревна и соящего на нем человека не превзойдет момента сил, создаваемых частью бревна, лежащего на краю обрыва. Обозначив за х расстояние от края обрыва до места, где находится человек, можно написать следующее соотношение для моментов сил:

Решая это уравнение относительно х получим:

В каких единицах измеряется момент силы

Положительный знак приписывают моментам

Правило рычага. Рычаг находится в равновесии когда действующие силы

Правильное выражение для момента силы

Как изменится момент силы если плечо увеличится в 2 раза, а сила увеличится в 2 раза

Могут ли весы (Рис.1.) быть в равновесии при F₂=0

Если Вы закончили работу с тестом, нажмите на кнопку «Результат тестирования», и Вы узнаете свой уровень знаний и количество правильных ответов.

mikahome.narod.ru

Момент силы: правило и применение

Почти две тысячи лет просуществовало правило рычага, открытое Архимедом еще в третьем веке до нашей эры, пока в семнадцатом веке с легкой руки французского ученого Вариньона не получило более общую форму.

Правило момента сил

Было введено понятие момента сил. Момент силы – это физическая величина, равная произведению силы на ее плечо:

M=Fl,

где M – момент силы,
F – сила,
l – плечо силы.

Из правила равновесия рычага напрямую вытекает правило моментов сил:

F1 / F2 = l2 / l1 или, по свойству пропорции F1 * l1= F2 * l2, то есть M1 = M2

В словесном выражении правило моментов сил звучит следующим образом: рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки. Правило моментов сил справедливо для любого тела, закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы. Потом из точки, в которой находится ось вращения, проводят перпендикуляр до линии действия силы. Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо, получаем значение момента силы относительно оси вращения. То есть, мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.

Применение правила моментов сил в различных ситуациях

Отсюда вытекает применение правила моментов сил в различных ситуациях. Например, если мы открываем дверь, то толкать ее мы будем в районе ручки, то есть, подальше от петель. Можно проделать элементарный опыт и убедиться, что толкать дверь тем легче, чем дальше мы прилагаем силу от оси вращения. Практический эксперимент в данном случае прямо подтверждается формулой. Так как, дабы моменты сил при разных плечах были равны, надо, чтобы большему плечу соответствовала меньшая сила и наоборот, меньшему плечу соответствовала большая. Чем ближе к оси вращения мы прилагаем силу, тем она должна быть больше. Чем дальше от оси мы воздействуем рычагом, вращая тело, тем меньшую силу нам необходимо будет приложить. Числовые значения легко находятся из формулы для правила моментов.

Именно исходя из правила моментов сил мы берем лом или длинную палку, если нам надо приподнять что-то тяжелое, и, подсунув под груз один конец, тянем лом возле другого конца. По этой же причине шурупы мы вворачиваем отверткой с длинной ручкой, а гайки закручиваем длинным гаечным ключом.

За единицу момента силы принят ньютон на метр (1 Н/м). это момент силы 1 ньютон, имеющей плечо в 1 метр.

www.nado5.ru

Что такое момент силы

Единицы измерения момента силы:

С вращателным движением объектов неразрывно связано понятие приложения момента силы.

Наверняка, многие знают жизненную аксиому — чем длиннее рычаг, тем легче сдвинуть груз. Если переложить этот процесс на язык физики, то можно сказать, что применение силы с помощью рычага характеризуется моментом силы.

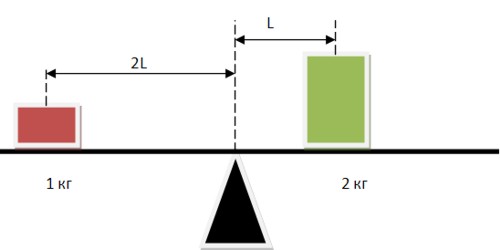
Для уравновешивания весов-качелей, изображенных на рисунке, важна не только величина прикладываемой силы, но и место, где она приложена. Расстояние от точки приложения силы до точки вращения называется плечом силы.

Никогда не задумывались над вопросом, почему нельзя открыть дверь, если толкать ее в месте крепления (у петель)?

Предположим, что перед нами стоит задача открыть дверь шириной 1 метр при помощи силы в 100 Н. Силу будем прикладывать в трех местах:

• F1 — возле петель (L=0);
• F2 — посредине двери (L2=0,5 м);
• F3 — у края двери (L3 = 1 м).

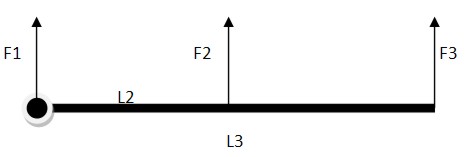
В первом случае, поскольку плечо силы равно нулю, произведение этого плеча на силу любой величины даст нулевой момент силы (поэтому, дверь нельзя открыть, толкая ее у петель).

Во втором случае:

Во третьем случае:

Из сказанного выше можно сделать вывод, что увеличение в два раза длины плеча при одной и той же прикладываемой силе дает такое же увеличение момента силы (проигрываем в расстоянии — выигрываем в силе, и наоборот: выигрываем в расстоянии — проигрываем в силе).

Рассмотрим вариант, когда сила прикладывается под углом.

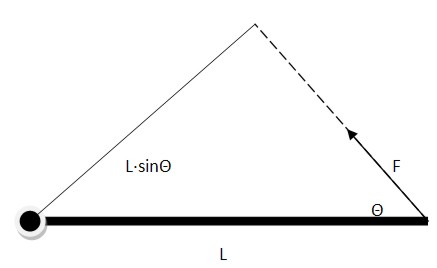
Как в таком случае вычислить необходимый момент силы для открытия дверей, ведь определить плечо сил, как это было раньше, не получится.

Чтобы решить поставленную задачу, необходимо руководствоваться правилом: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Для определения плеча силы необходимо продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения. Получился прямоугольный треугольник, используя тригонометрические функции, можно найти искомое плечо силы: L·sinΘ

Предположим, что сила приложена под углом Θ = 45°

Исходя из вышесказанного, становится понятным, что открыть дверь не удастся, если приложить силу с углом Θ = 0°, т.е., параллельно двери (в ее торец). Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение (говорят, что у такой силы нет ненулевого плеча для создания вращательного момента силы).

Момент силы является векторной величиной. Направление действия момента силы вычисляется по правилу правой руки (аналогично определению направления вектора угловой скорости).

Правило правой руки: если ладонью правой руки охватить ось вращения, таким образом, чтобы пальцы руки совпадали с направлением приложенной силы, то, вытянутый большой палец будет указывать направление вектора момента силы.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:

prosto-o-slognom.ru