Правила построения отрицаний высказываний, содержащих кванторы

Рассмотрим высказывание: «Все натуральные числа делятся на 3». В том, что это ложное высказывание, легко убедиться, приведя контрпример. Так, натуральное число 17 не делится на 3.

Построим отрицание данного высказывания. Можно сказать: «Неверно, что все натуральные числа делятся на 3». Это предложе­ние истинное, и по смыслу оно совпадает с предложением «Суще­ствуют натуральные числа, которые не делятся на 3».

Таким образом, отрицание высказывания «Все натуральные числа делятся на 3» можно построить двумя способами:

1) поставив перед данным предложением слова «неверно, что»;

2) заменив квантор общности на квантор существования, а предложение, стоящее после квантора, его отрицанием.

Заметим, что предложение «Все натуральные числа не делятся на 3» не является отрицанием высказывания «Все натуральные числа делятся на 3», поскольку оно ложно так же, как и данное высказывание.

Возьмем теперь предложение с квантором существования: «Некоторые нечетные числа делятся на 4». Это ложное высказы­вание: все нечетные числа не делятся на 2 и, следовательно, не делятся на 4.

Построим отрицание данного высказывания. Можно сказать: «Неверно, что некоторые нечетные числа делятся на 4». Это предложение истинное в по смыслу совпадает с таким: «Все не­четные числа не делятся на 4».

Таким образом, отрицание высказывания «Некоторые нечетные числа делятся на 4» можно построить двумя способами:

2) заменив квантор существования на квантор общности, а предложение, стоящее после квантора, его отрицанием.

При построении отрицаний высказываний мы воспользовались правилом, которое принимаем без доказательства.

Отрицание высказывания с квантором (общности или существования) может быть построено двумя способами:

1) перед данным высказыванием ставятся слова «неверно, что»;

studopedia.org

Правило построение отрицания

Кванторы общности и существования.

Построение отрицания высказываний, содержащих кванторы.

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание. Чаще всего упоминают:

· Квантор всеобщности (обозначение: · Квантор существования (обозначение: 1/Temp/msohtmlclip1/01/clip_image003.gif» />
Отрицанием высказывания с квантором общности (1/Temp/msohtmlclip1/01/clip_image005.gif» />х) Р(х) является высказывание (1/Temp/msohtmlclip1/01/clip_image006.gif» />х) 1/Temp/msohtmlclip1/01/clip_image007.gif» />, а отрицанием высказывания с квантором существования (1/Temp/msohtmlclip1/01/clip_image006.gif» />х) Р(х) – высказывание (1/Temp/msohtmlclip1/01/clip_image005.gif» />х) Для отрицания высказывания с двумя переменными (1/Temp/msohtmlclip1/01/clip_image005.gif» />х)(1/Temp/msohtmlclip1/01/clip_image006.gif» />у)
Р(х; у)используется следующая формула: (1/Temp/msohtmlclip1/01/clip_image006.gif» />х)(1/Temp/msohtmlclip1/01/clip_image005.gif» />у) 3. Отрицание высказываний и высказывательных форм

Пусть предложение А – высказывание. Если перед сказуемым данного предложения поставить частицу «не» либо перед всем предложением поставить слова «неверно, что», то получится новое предложение, которое называется отрицанием данного и обозначается (читают: «не А» или «неверно, что А»).

Определение. Отрицанием высказывания А называется высказывание , которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.

Таблица истинности отрицания имеет вид:

Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.

Построим, например, отрицание ложного высказывания «число 28 делится на 9»:

а) Число 28 не делится на 9.

б) Неверно, что число 28 делится 9.

Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.

Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний. Если перед всем составным высказыванием поставить слова «неверно, что», то, безусловно, получим его отрицание. А как быть с частицей «не»? Можно ли поставить ее перед сказуемым составного предложения и получить его отрицание? Возьмем, например, высказывание «число 28 делится на 9 и на 4». Оно ложное, так как представляет собой конъюнкцию двух высказываний, одно из которых ложно. Поставив перед сказуемым этого высказывания частицу «не», получим конъюнкцию «число 28 не делится на 9 и на 4», в которой одно из предложений «число 28 не делится на 4» – ложное и, значит, ложно построенное с помощью частицы «не» предложение. Поэтому оно не является отрицанием высказывания «число 28 делится на 9 и на 4».

Можно доказать, что отрицание конъюнкции двух высказываний А и В является дизъюнкцией их отрицаний. Для этого надо убедится в том, что значения истинности высказываний вида 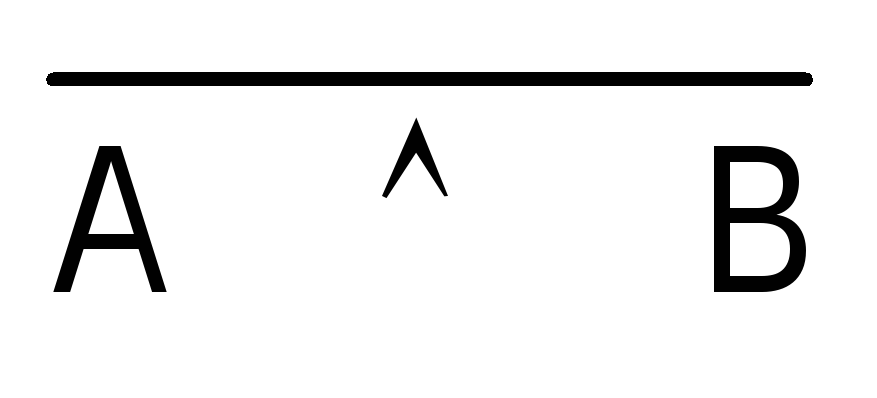и  совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:



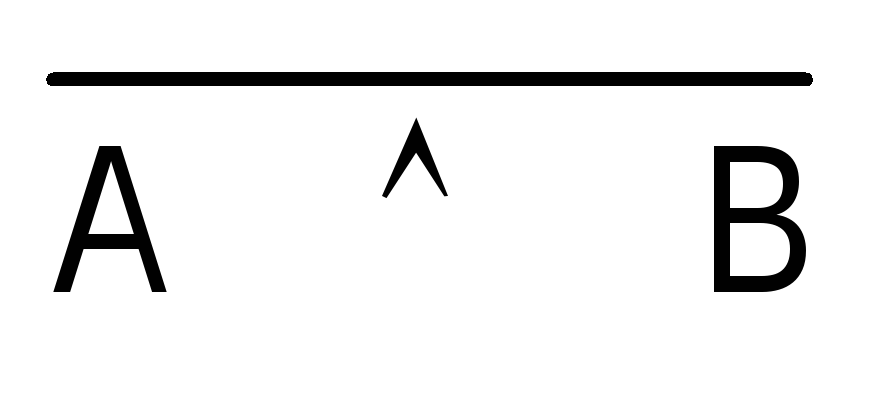
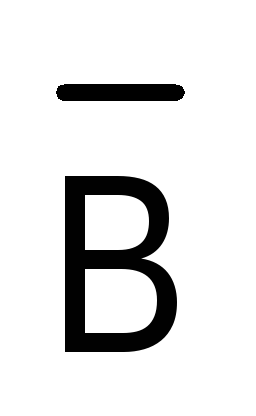
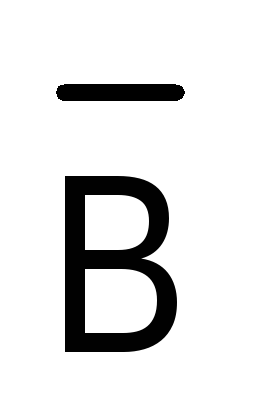
Про высказывания вида и 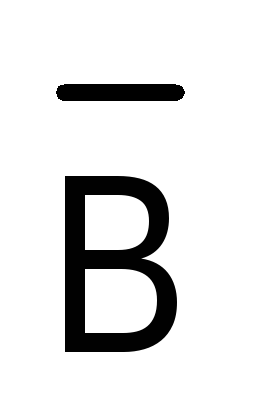 говорят, что ониравносильны, и пишут   .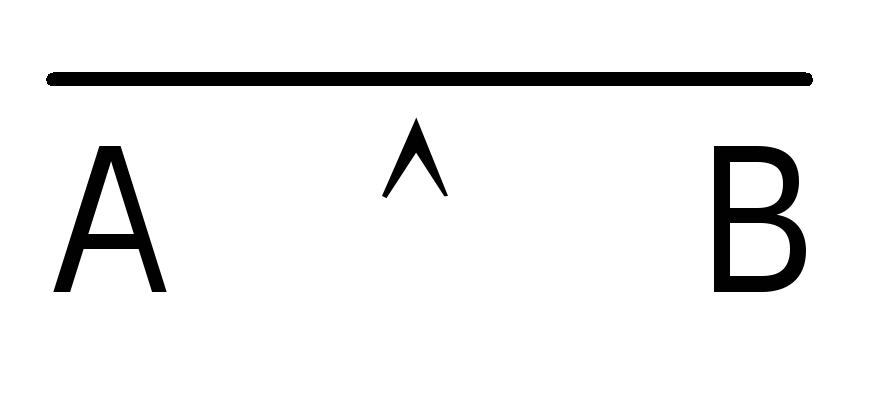

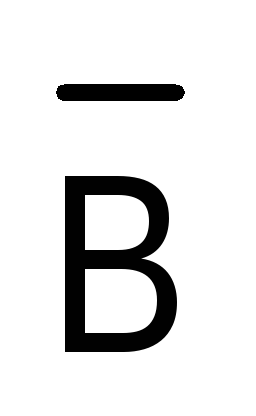Аналогично можно доказать, что имеет место равносильность  .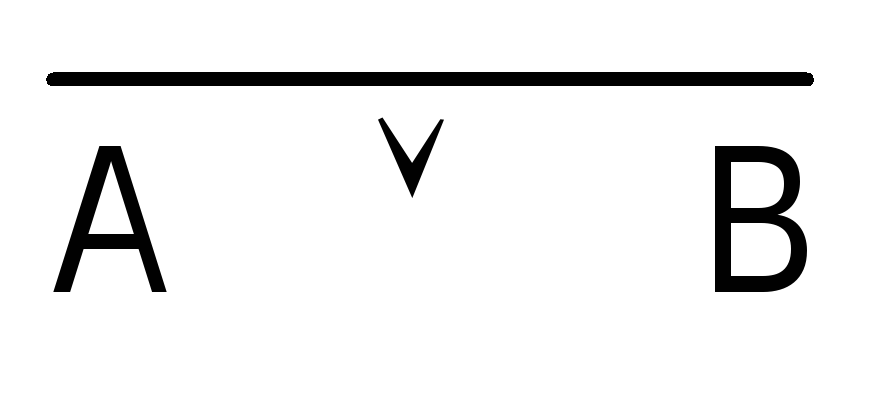

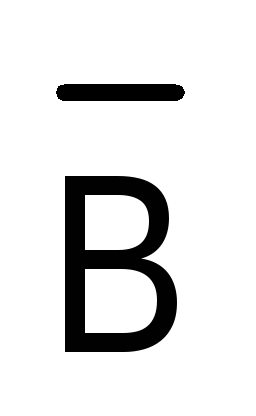Эти равносильности носят название законов де Моргана.

Из них вытекает следующее правило построения отрицания конъюнкции и дизъюнкции: чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и»).

Задача 1. Построить отрицание высказывания «число 28 делится на 9 или на 6».

Решение (два способа).

Поставим перед данным высказыванием слова «неверно, что». Получим высказывание «неверно, что число 28 делится на 6 или на 6», которое является отрицанием исходного.

Воспользуемся законом де Моргана: заменим высказывания «число 28 делится на 9» и «число 28 делится на 6» их отрицаниями, а союз «или» поменяем на союз «и». Получим высказывание «число 28 не делится на 9 и не делится на 6», которое также является отрицанием исходного.

Итак, мы выяснили, как строить отрицание конъюнкции и дизъюнкции высказываний. А как быть с высказываниями, которые содержат кванторы? Достаточно ли для отрицания таких предложений поставить перед сказуемым частицу «не»? Например, будет ли отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» предложение «всякий прямоугольный треугольник не является равнобедренным»? Видим, что не будет, так как оба высказывания ложны. Таким образом, строить отрицания высказываний с квантором при помощи частицы «не» перед сказуемым нельзя.

Остается другой путь – перед всем предложением, ставим слова «неверно, что». Тогда отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» будет предложение «неверно, что всякий прямоугольный треугольник является равнобедренным», но это предложение имеет тот же смысл, что и предложение «некоторые прямоугольные треугольники не являются равнобедренными».

Отрицанием высказывания «некоторые прямоугольные треугольники являются равнобедренными» является высказывание «неверно, что некоторые прямоугольные треугольники являются равнобедренными».

Вообще если дано предложение (х) А(х), то его отрицанием будут предложения 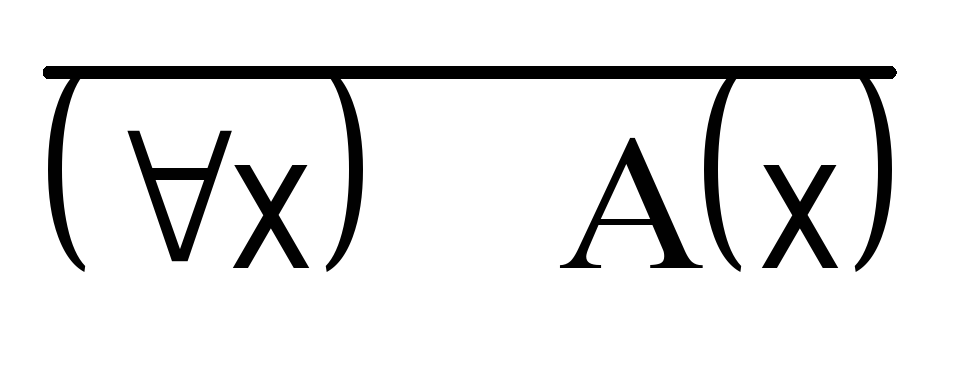и (х) , также имеющие один и тот же смысл (и одно и то же значение истинности).

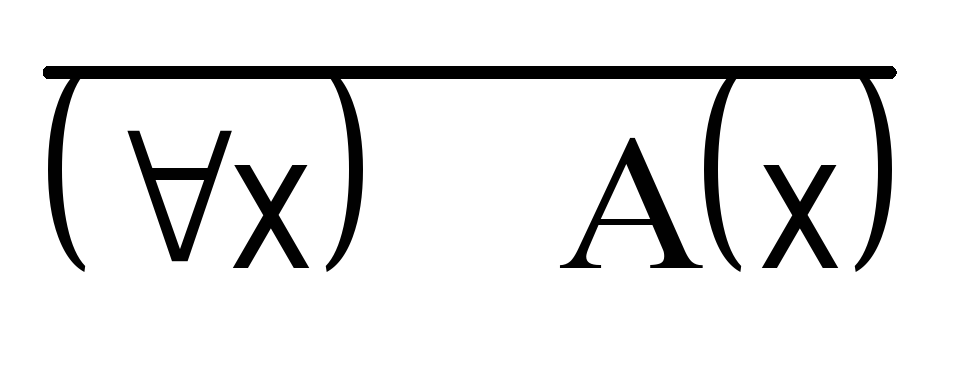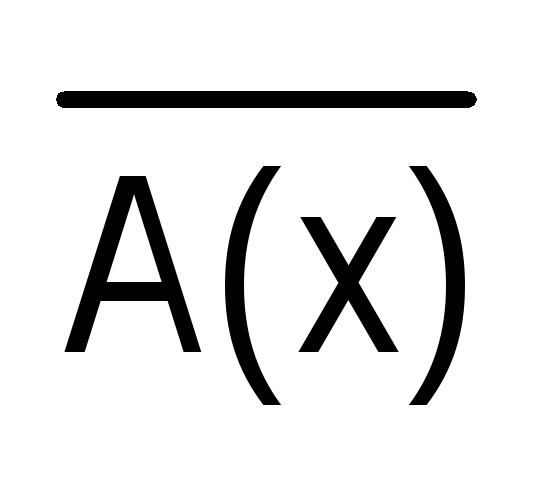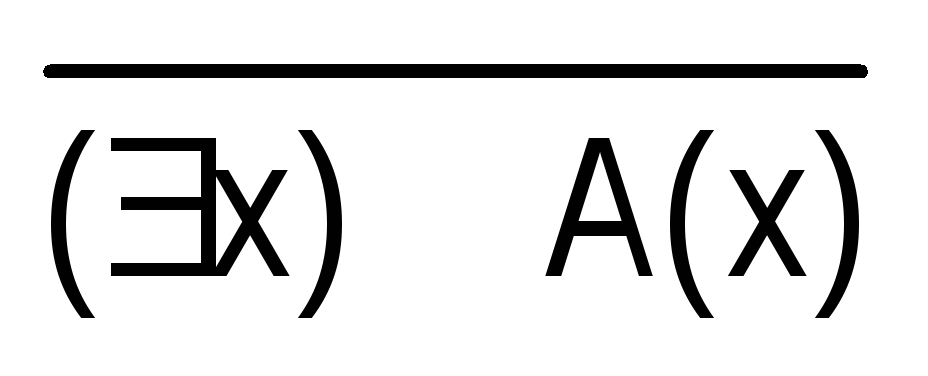Получаем две равносильности:  (х) ;

 х) .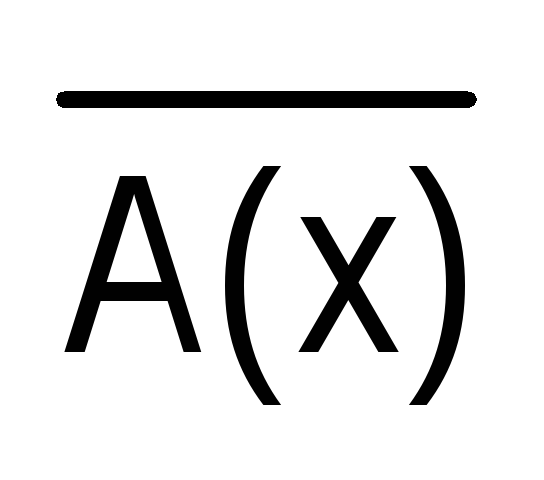

Из них вытекает правило: для того чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.

Задача 2. Построить отрицание высказывания «некоторые однозначные числа делятся на 10».

Решение. Сделать это можно двумя способами.

Поставим перед высказыванием слова «неверно, что». Получим высказывание «неверно, что некоторые однозначные числа делятся на 10», которое является отрицанием данного.

Заменим квантор существования (он выражен словом «некоторые») на квантор общности «все» и построим отрицание предложения, стоящего после слова «некоторые», поставив частицу «не» перед сказуемым. Получим высказывание «все однозначные числа не делятся на 10».

Последнее, о чем пойдет речь, — это отрицание высказывательных форм.

Пусть на множестве Х задана высказывательная форма А(х). Ее отрицание обозначим 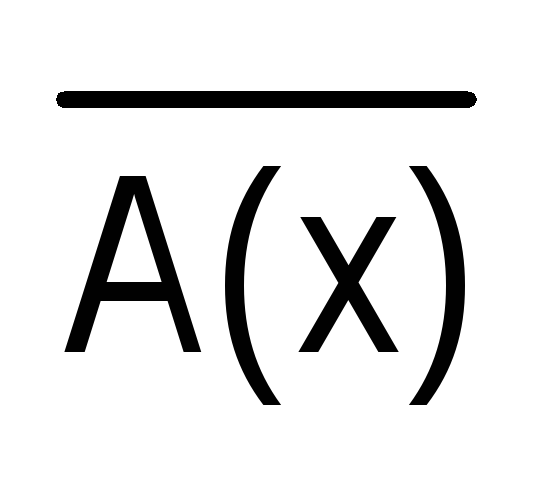(читают: «не А(х)» или «неверно, что А(х)»). Предложение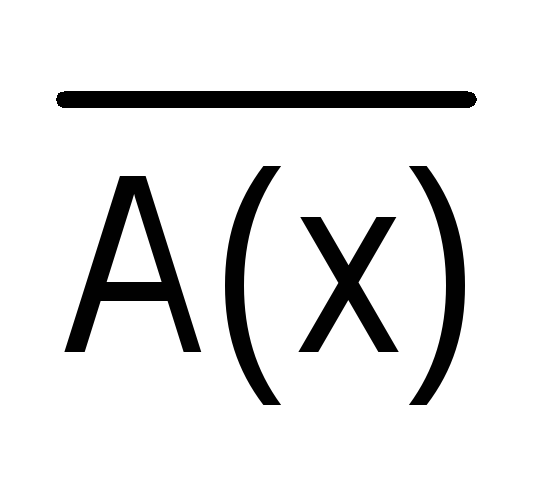будет обращаться в истинное высказывание лишь при тех значениях х из множества Х, при которых А(х) – ложно. Таким образом,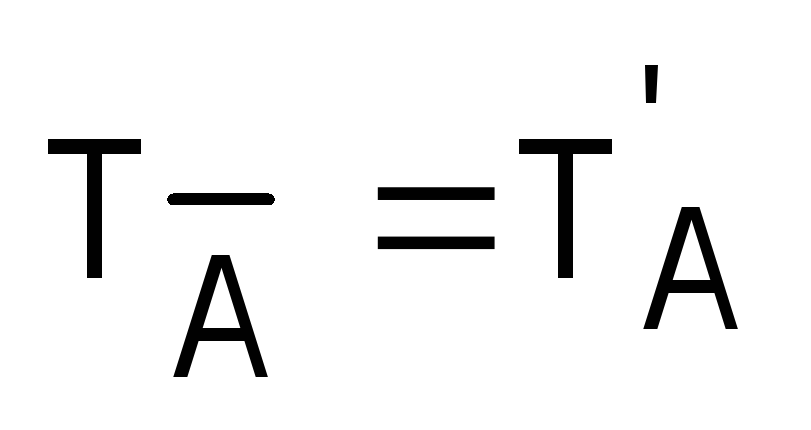, где — множество истинности предложения 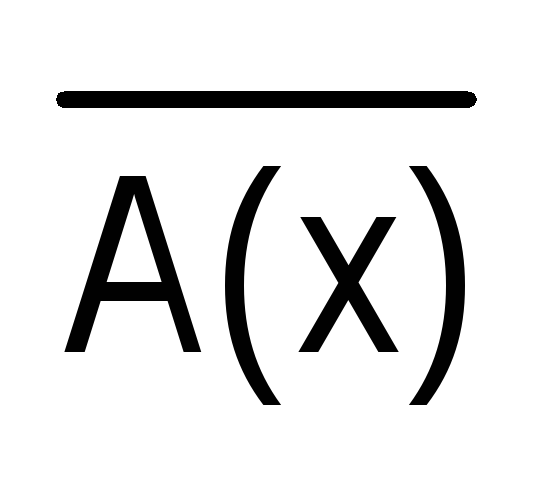, а– дополнение множества Т_А до множества Х.

Доказательство этого равенства мы опускаем.

Пусть, например, на множестве натуральных чисел задана высказывательная форма А(х) – «число х кратно 5». Тогда ее отрицанием будет предложение «число х не кратно 5» (или «неверно, что число х кратно 5»), истинное при всех значениях х, которые не кратны 5.

studfiles.net

Отрицание в английском языке

Чтобы не пропустить новые полезные материалы, подпишитесь на обновления сайта

Любые предложения в английском языке – повествовательные, вопросительные, повелительные – могут быть как утвердительными, так и отрицательными (подробнее о типах предложений читайте в статье «Типы предложений в английском языке»). Но если с утверждением все более-менее ясно, то отрицание в английском языке следует разъяснить. Необходимо запомнить, с помощью каких средств выражается отрицание, употребление каких конструкций подразумевает и насколько сильно отличается от того же аспекта в языке русском.

Как выразить отрицание в английском языке?

Отрицательные предложения в английском языке формируются при помощи определенных языковых элементов. Самым главным элементом отрицания в английском языке является частица not. Ставить ее следует после вспомогательного или модального глагола. Если же вспомогательных глаголов несколько, то после первого из них.

He will not go to the party. — Он не пойдет на вечеринку.

We have not discussed this question yet. — Мы еще не обсудили этот вопрос.

Помимо этой частицы для выражения отрицания в английском языке в простом настоящем и прошедшем временах (Present Simple and Past Simple) следует использовать вспомогательный глагол do / does / did соответственно.

She does not want us to join her. — Она не хочет, чтобы мы к ней присоединились.

I did not expect you to come so early. — Я не ожидал, что ты придешь так рано.

Если же в роли сказуемого в предложении употреблен глагол be, вспомогательный глагол не потребуется. То же касается и глагола have, если только он не является модальным в данном случае или не образует устойчивые словосочетания. Тем не менее, в американском варианте английского языка, с глаголом to have для выражения отрицания тоже принято использовать вспомогательный глагол do.

You are not a man of my life. — Ты не мужчина моей жизни.

You have no friends in this city. — You do not have any friends in this city. — У вас нет друзей в этом городе. (оба варианта верны)

Также отметьте, что частица not может относиться и к неличной форме глагола.

Not feeling well, she decided to stay at home. — Она решила остаться дома, так как плохо себя чувствовала.

Для выражения отрицания в английском языке помимо основного элемента – частицы not – вы можете использовать и другие слова. К ним относятся: отрицательные местоимения (no, nobody, nothing, nowhere, none); союз neither…nor; наречия hardly, scarcely, never; предлог without.

На этом этапе я не привожу примеры с этими словами по одной причине – чтобы грамотно их употреблять, необходимо знать одну самую главную особенность отрицания в английском языке. Эта особенность касается множественного отрицания, явления, которое очень распространено в русском. Возьмем русское предложение: «Она никогда ему ничего не расскажет».

Совершенно нормально предложение, свободно существующее в русском. Это, например, ваше обещание другому человеку не открывать его секрет. В этом предложении без проблем уживаются целых три отрицания: наречие, местоимение и частица. Если мы также переведем это предложение на английский, получим что-то невероятное. Пробуем? She will never not tell him nothing.

Конечно, это же предложение можно сказать и по-другому, но я предложила именно кальку, чтобы показать, что данная грамматическая конструкция для английского языка в корне неверна. Сколько бы отрицаний не было в русском варианте, в английском будет лишь одно. И вы можете выбрать, что именно «отрицательное» вы используете, но только одно. Вот то же предложение:

• She will never tell him anything.
• She will not tell him anything then.
• She will tell him nothing.

Как вы видите, все другие «отрицательные» элементы предложения помимо основного выражаются с помощью местоимений на any.

Все приведенные примеры отрицания в английском языке прописаны полностью, без наличия сокращенных форм. А они есть, и их стоит знать:

engblog.ru

Статья: «Построение математических рассуждений (правило заключения, правило отрицания, правило силлогизма)»

Построение математических рассуждений

(правило заключения, правило отрицания, правило силлогизма)

Свойства основных понятий раскрываются в аксиомах – предложениях, принимаемых без доказательства.

Например, в школьной геометрии есть аксиомы: «через любые две точки можно провести прямую и только одну» или «прямая разбивает плоскость на две полуплоскости».

Система аксиом любой математической теории, раскрывая свойства основных понятий, дает их определения. Такие определения называют аксиоматическими.

Доказываемые свойства понятий называют теоремами, следствиями, признаками, формулами, правилами.

Доказать теорему А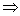В – это значит установить логическим путем, что всегда, когда выполняется свойство А, будет выполняться свойство В.

Доказательством в математике называют конечную последовательность предложений данной теории, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предложений этой последовательности по правилам логического вывода.

В основе доказательства лежит рассуждение – логическая операция, в результате которой из одного или нескольких взаимосвязанных по смыслу предложений получается предложение, содержащее новое знание.

В качестве примера рассмотрим рассуждение школьника, которому надо установить отношение «меньше» между числами 7 и 8. Учащийся говорит: «7

Ни одно А не есть В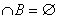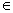

А

аА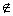

а

аА

а

Покажем, что умозаключение, выполненное по правилу заключения, является дедуктивным. Сначала запишем это правило на теоретико-множественном языке.

Посылка А(х)В(х) может быть записана в виде ТАТВ, где ТА и ТВ – множества истинности высказывательных форм А(х) и В(х).

Частная посылка А(а) означает, что аТА, а заключение В(а) показывает, что аТВ.

Все умозаключение , построенное по правилу заключения, запишется на теоретико-множественном языке так: .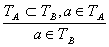

Неполная индукция – это умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.

Неполная индукция не является дедуктивным умозаключением, поскольку, рассуждая по такой схеме, можно прийти к ложному выводу.

Например, рассмотрим такие выражения: 3 + 5 и 3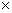5; 2 + 7 и 27. Видим, что 3 + 5 12.

Поэтому выводы, полученные с помощью неполной индукции, необходимо либо доказывать, либо опровергать.

Пример 3. При обучении делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значение выражения 12 : 4, следует узнать, на какое число надо умножить делитель 4, чтобы получить делимое 12. Известно, что 43 = 12. Значит, 12 : 4 = 3.

Данный пример – это пример рассуждения по аналогии.

Под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.

Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.

urokimatematiki.ru