ЛАБОРАТОРНАЯ РАБОТА №107
Проверка основного уравнения динамики
вращательного движения
Цель работы: Экспериментальная проверка основного закона динамики вращательного движения с помощью маятника Обербека.
Приборы и принадлежности: маятник Обербека с миллисекундомером FРМ – 15, штангенциркуль.
Теоретическое введение
При рассмотрении вращения твердого тела с динамической точки зрения наряду с понятием о силах вводится понятие о моментах сил и наряду с понятием о массе – понятие о моменте инерции.
Пусть материальная точка массой т под действием внешней силы 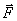 движется криволинейно относительно неподвижной точки О. На материальную точку действует момент силы и точка обладает моментом импульса. Положение движущейся материальной точки определяется радиус-вектором
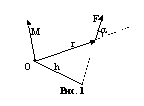
движется криволинейно относительно неподвижной точки О. На материальную точку действует момент силы и точка обладает моментом импульса. Положение движущейся материальной точки определяется радиус-вектором 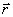 , проведенным к ней из точки О (рис.1). Моментом силы
, проведенным к ней из точки О (рис.1). Моментом силы 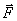 относительно неподвижной точки О называется векторная величина
относительно неподвижной точки О называется векторная величина 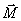 , равная векторному произведению радиус-вектора
, равная векторному произведению радиус-вектора 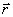 вектор силы
вектор силы 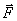

Вектор 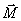 направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов 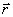 и
и 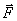 и его направление соответствует правилу правого винта. Модуль момента сил равен
и его направление соответствует правилу правого винта. Модуль момента сил равен
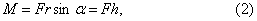
где a — угол между векторами 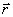 и
и 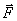 , h=rsin a — плечо силы, равное кратчайшему расстоянию от точки О до линии действия (вдоль которой действует сила) силы
, h=rsin a — плечо силы, равное кратчайшему расстоянию от точки О до линии действия (вдоль которой действует сила) силы 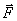 .
.
Моментом импульса 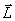 относительно точки О называется векторная величина, равная векторному произведению радиуса вектора
относительно точки О называется векторная величина, равная векторному произведению радиуса вектора 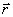 на вектор импульса
на вектор импульса 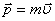 , то есть
, то есть
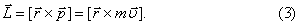
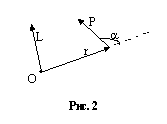
Вектор 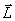 направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов 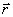 и
и 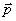 (рис.2). Модуль момента импульса равен
(рис.2). Модуль момента импульса равен

где b — угол между направлением векторов 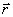 и
и 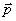 .
.
Основной закон динамики вращательного движения
Пусть механическая система, состоящая из N материальных точек под действием внешних сил, результирующая которых 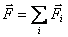 , совершает криволинейное движение относительно неподвижной точки О, то есть
, совершает криволинейное движение относительно неподвижной точки О, то есть

где 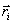 — радиус-вектор, проведенный от точки О до i-ой материальной точки,
— радиус-вектор, проведенный от точки О до i-ой материальной точки, 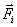 — вектор силы, действующей на i-ую материальную точку.
— вектор силы, действующей на i-ую материальную точку.
Также можно найти момент импульса системы
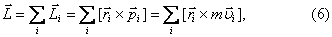
где 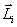 — момент импульса i-ой материальной точки.
— момент импульса i-ой материальной точки.
Момент импульса 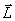 зависит от времени t, так как скорость является функцией от времени. Взяв производную от момента импульса системы по времени t, получим
зависит от времени t, так как скорость является функцией от времени. Взяв производную от момента импульса системы по времени t, получим

Формула (7) является математическим выражением основного закона динамики вращательного движения системы, согласно которому скорость изменения момента импульса системы по времени равна результирующему моменту внешних сил, действующих на систему.
Закон (7) справедлив и для твердого тела, т.к. твердое тело можно рассматривать как совокупность материальных точек.
Пусть в частном случае твердое тело вращается относительно неподвижной оси, проходящей через центр масс, под действием внешней силы 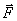 . Твердое тело разбиваем на материальные точки. Для материальной точки массой mi уравнение движения запишется
. Твердое тело разбиваем на материальные точки. Для материальной точки массой mi уравнение движения запишется

Момент импульса 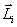 для i – ой материальной точки равен
для i – ой материальной точки равен

Поскольку при вращательном движении b = 90 0 , то и линейная скорость 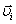 связана с угловой скоростью
связана с угловой скоростью 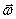 формулой
формулой 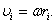 Тогда (9) можно записать в виде
Тогда (9) можно записать в виде

Величина  представляет собой момент инерции материальной точки относительно оси Z. Тогда (10) примет вид
представляет собой момент инерции материальной точки относительно оси Z. Тогда (10) примет вид

С учетом (11) основной закон динамики вращательного движения твердого тела относительно неподвижной оси запишется
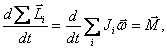
где 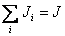 — момент инерции твердого тела относительно оси Z.
— момент инерции твердого тела относительно оси Z.
При 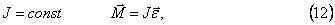
где 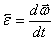 — угловое ускорение. Согласно основному уравнению динамики вращательного движения (12) результирующий момент внешней силы, действующей на тело, равен произведению момента инерции J тела на его угловое ускорение.
— угловое ускорение. Согласно основному уравнению динамики вращательного движения (12) результирующий момент внешней силы, действующей на тело, равен произведению момента инерции J тела на его угловое ускорение.
Из уравнения (12) следует, что при J = const угловое ускорение тела
прямо пропорционально моменту внешних сил относительно оси вращения, т.е.
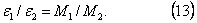
При M = const угловое ускорение обратно пропорционально моменту инерции тела, т.е.
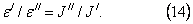
Целью настоящей работы является проверка соотношений (13) и (14), а, следовательно, и основного уравнения динамики вращательного движения (12), следствиями которого они являются.
Описание рабочей установки и метода измерений
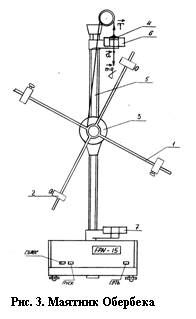
Для проверки соотношений (13) и (14) используется маятник Обербека, представляющий собой инерционное колесо в виде крестовины. На четырех взаимно перпендикулярных стержнях 1 расположены четыре одинаковых цилиндрических груза 2, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси. Грузы закрепляются симметрично, т.е. так, чтобы их центр масс совпадал с осью вращения. На горизонтальной оси крестовины имеется двухступенчатый диск 3, на который наматывается нить. Один конец нити прикреплен к диску, а ко второму концу нити подвешен груз 4, под действием которого прибор приводится во вращение. Общий вид маятника Обербека FРМ-06 изображен на рис.3. Для удержания системы крестовины вместе с грузами в состоянии покоя используется тормозной электромагнит. С целью отсчета высоты падения грузов на колонне нанесена миллиметровая шкала 5. Время падения груза 4 измеряется миллисекундомером FРМ-15, к которому подключены фотоэлектрические датчики №1(6) и №2(7). Фотоэлектрический датчик №2(7) вырабатывает электроимпульс конца измерений времени и включает тормозной электромагнит.
Если предоставить возможность грузу 4 двигаться, то это движение будет происходить с ускорением a.

где t— время движения груза с высоты h. При этом шкив со стержнями и находящимися на них грузами будет вращаться с угловым ускорением e .

где r— радиус шкива.
Вращающий момент силы, приложенной к крестовине и сообщающий угловое ускорение вращающейся части прибора, находим по формуле

где Т— сила натяжения шнура. По второму закону Ньютона для груза 4 имеем


где g— ускорение свободного падения.
Из формул (12), (15), (16), (17) и (19) имеем
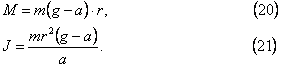
Порядок выполнения работы и обработка результатов измерений
1. Измерить штангенциркулем радиус большого и малого шкивов r1 и r2.
2. Определить массу груза 4 взвешиванием на технических весах с точностью ± 0,1 г.
3. Проверить соотношение (13). Для этого:
— закрепить цилиндрические подвижные грузы на стержнях на ближайшем расстоянии от оси вращения так, чтобы крестовина была в положении безразличного равновесия;
— намотать нить на большой шкив радиуса r 1 и измерить время движения груза t с высоты h миллисекундомером, для чего
— включить сетевой шнур измерителя в сеть питания;
— нажать клавишу «СЕТЬ» и проверить, показывают ли все индикаторы измерителя нуль и горят ли все индикаторы обоих фотоэлектрических датчиков;
— переместить груз в верхнее положение и проверить, находится ли схема в состоянии покоя;
— нажать клавишу «ПУСК» и миллисекундомером измерить время движения груза;
— нажать клавишу «СБРОС» и проверить, произошло ли обнуление показаний измерителя и освобождение блокировки электромагнитом;
— переместить груз в верхнее положение, отжать клавишу «ПУСК» и проверить, произошла ли повторная блокировка схемы;
— опыт повторить 5 раз. Высоту h не рекомендуется менять в течение всей работы;
— не меняя расположения подвижных грузов и оставляя тем самым неизменным момент инерции системы, опыт повторить, наматывая нить с грузом на малый шкив радиусом r 2 ;
— проверить справедливость следствия основного закона динамики вращательного движения:
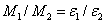 , при
, при 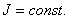
— данные результатов измерений и вычислений занести в таблицы 1 и 2.
4. Проверить соотношение (1 4 ). Для этого:
— раздвинуть подвижные грузы до упоров на концах стержней, но так, чтобы крестовина снова была в положении безразличного равновесия;
— для малого шкива r 2 определить время движения груза t / по данным 5 опытов;
— по формулам (15), (20), (21) определить значения a / , e / , J1;
— при проверке соотношения 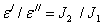 при
при 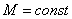 можно пользоваться значениями предыдущего опыта, положив
можно пользоваться значениями предыдущего опыта, положив 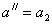 и
и 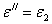 ;
;
— по формуле (21) определить значение J2;
— вычислить значения 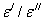 и
и 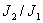 .
.
— Результаты измерений и вычислений занести в таблицу 3.
phys-bsu.narod.ru
I.4.2 ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Твёрдое тело, вращающееся вокруг некоторых осей, проходящих через центр масс, если оно освобождено от внешних воздействий, сохраняет вращение неопределённо долго. (Это заключение аналогично первому закону Ньютона для поступательного движения).
Возникновение вращения твёрдого тела всегда вызывается действием внешних сил, приложенных к отдельным точкам тела. При этом неизбежно возникновение деформаций и появление внутренних сил, обеспечивающих в случае твёрдого тела практическое сохранение его формы. При прекращении действия внешних сил вращение сохраняется: внутренние силы не могут ни вызвать, ни уничтожить вращение твёрдого тела.
Результатом действия внешней силы на тело, имеющее неподвижную ось вращения, является ускоренное вращательное движение тела. (Это заключение аналогично второму закону Ньютона для поступательного движения).
Основной закон динамики вращательного движения: в инерциальной системе отсчёта угловое ускорение 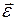 , приобретаемое телом, вращающимся относительно неподвижной оси, пропорционально суммарному моменту всех внешних сил
, приобретаемое телом, вращающимся относительно неподвижной оси, пропорционально суммарному моменту всех внешних сил 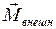 , действующих на тело, и обратно пропорционально моменту инерции тела
, действующих на тело, и обратно пропорционально моменту инерции тела 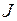 относительно данной оси:
относительно данной оси:
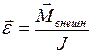 . (I.109)
. (I.109)
Можно дать и более простую формулировку основному закону динамики вращательного движения (его ещё называют вторым законом Ньютона для вращательного движения): вращающий момент равен произведению момента инерции на угловое ускорение:
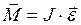 . (I.110)
. (I.110)
Моментом импульса 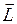 (моментом количества движения, угловым моментом) тела называется произведение его момента инерции
(моментом количества движения, угловым моментом) тела называется произведение его момента инерции 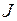 на угловую скорость
на угловую скорость 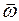 :
:
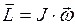 . (I.111)
. (I.111)
Момент импульса – векторная величина. Его направление совпадает с направлением вектора угловой скорости.
Изменение момента импульса определяется следующим образом:
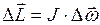 . (I.112)
. (I.112)
Изменение момента импульса  (при неизменном моменте инерции тела) может произойти, только вследствие изменения угловой скорости
(при неизменном моменте инерции тела) может произойти, только вследствие изменения угловой скорости 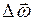 и всегда обусловлено действием момента силы
и всегда обусловлено действием момента силы 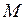 .
.
Согласно формуле 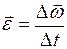 , а также формулам (I.110) и (I.112) изменение момента импульса можно представить в виде:
, а также формулам (I.110) и (I.112) изменение момента импульса можно представить в виде:
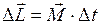 . (I.113)
. (I.113)
Произведение 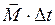 в формуле (I.113) называется импульсом момента силы или движущим моментом. Он равен изменению момента импульса.
в формуле (I.113) называется импульсом момента силы или движущим моментом. Он равен изменению момента импульса.
Формула (I.113) справедлива при условии, что момент силы не меняется с течением времени 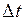 . Если же момент силы зависит от времени, т.е.
. Если же момент силы зависит от времени, т.е. 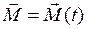 , то
, то
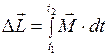 . (I.114)
. (I.114)
Формула (I.114) показывает, что: изменение момента импульса равно интегралу по времени от момента силы. Кроме того, если эту формулу представить в виде: 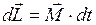 , то из неё будет следовать определение момента силы: мгновенный момент силы представляет собой первую производную момента импульса по времени,
, то из неё будет следовать определение момента силы: мгновенный момент силы представляет собой первую производную момента импульса по времени,
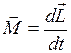 . (I.115)
. (I.115)
Выражение (I.115) является ещё одной формой основного уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси: производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.
В замкнутой системе момент внешних сил 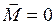 и
и 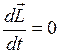 , следовательно:
, следовательно:
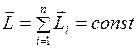 . (I.116)
. (I.116)
Формула (I.116) представляет собой закон сохранения момента импульса: векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем Закон сохранения момента импульса – фундаментальный закон природы.
Обратите внимание: полный момент импульса системы равен векторной сумме моментов импульса отдельных частей системы.
Дата добавления: 2016-09-06 ; просмотров: 46387 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
poznayka.org
ОСНОВНОЙ ЗАКОН ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Пусть твердое тело вращается вокруг неподвижной оси z (рис.1). При таком движении все точки тела описывают окружности, центры которых лежат на оси вращения. Поскольку векторы перемещения , скорость и ускорение различны для различных точек тела, для характеристики вращательного движения удобнее использовать угол поворота j, угловую скорость w , угловое ускорение e, одинаковые для всех точек твердого тела.
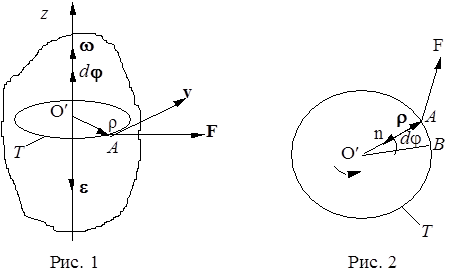
Рассмотрим движение точки A . Она движется по окружности Т, центр которой O¢ распологается на оси z . Для определения угла поворота j вектора r, определяющего положение точки А , введем неподвижную линию О¢B. Пусть rза время dt поворачивается на угол dj, в указанном направлении (рис.2). Представим малый угол поворота в виде вектора djнаправленного вдоль оси, и его направление определим следующим образом: если смотреть с конца вектора dj , вращение на угол dj видно происходящим против направления движения часовой стрелки.
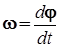 (1)
(1)
называется угловой скоростью. Она направлена вдоль оси, вокруг которой вращается тело, в сторону вектора dj. Изменение вектора угловой скорости со временем характеризуется величиной
e= 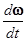 , (2)
, (2)
которую называют угловым ускорением.
Направление вектора e совпадает с направлением приращения вектора угловой скорости dw. Если dw > 0, то eи w направлены в одну сторону, а при dw 2 n ,
где at и an – тангенциальная и нормальная составляющие ускорения, n– единичный вектор, направленной по нормали к центру кривизны траектории 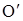 .
.
Чтобы твердое тело с закрепленной осью привести во вращательное движение, необходимо хотя бы в одной из его точек приложить внешнюю силу, не проходящую через ось вращения и не параллельную ей. Моментом силы F, приложенной в точке А перпендикулярно оси z , называется вектор
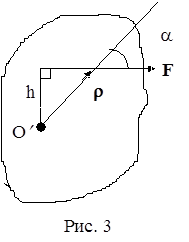
Мz = [rF], (4)
где r – вектор, указанный на рис.1 и 2. Его модуль определяется формулой
Здесь a — угол между векторами r и F, а величина h = r sin a — плечо силы (рис. 3). В частном случае a =p/2 получается
Моментом инерции материальной точки относительно оси z называется произведение ее массы mi на квадрат расстояния ri от материальной точки до оси вращения
Для определения момента инерции тела относительно оси его мысленно разбиваем на множество мелких частей. Момент инерции тела относительно оси z равен сумме моментов инерции его частей, то есть
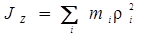 . (8)
. (8)
Основной закон динамики вращательного движения твердого тела вокруг неподвижной оси z записывается в виде
Этот закон может быть проверен с помощью маятника Обербека.
Если сравнить (9) со вторым законом Ньютона для материальной точки
F = am , (10)
можно увидеть их сходство. Если в (10) заменить линейное ускорение aугловым ускорением e, массу m моментом инерции JZ и силу моментом силы, то получится уравнение (9). Поэтому можно говорить, что инертность тела во вращательном движении характеризуется его моментом инерции.
Описание установки
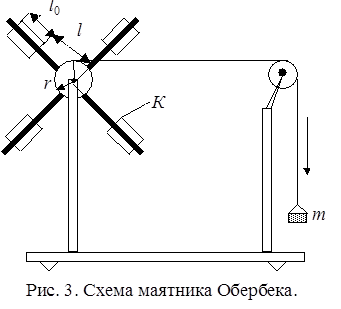
Маятник Обербека (рис.3) представляет собой крестовину из четырех стержней с делениями, прикрепленных ко втулке с осью. На стержни надеваются цилиндры К массой M, которые могут быть закреплены на разных расстояниях l от оси вращения. Шкив радиусом r насажен на ось вращения маятника. На шкив наматывается нить, перекинутая через блок. На конце нити подвешивается груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза определяется по шкале с делениями.
Момент силы Мz, под действием которого маятник приводится во вращательное движение, определяется по формуле
где Fн – сила натяжения нити, r – радиус шкива. Для определения силы натяжения нити запишем второй закон Ньютона P – Fн = m a , где P =mg – сила тяжести груза. Отсюда следует
Из (11) и (12) следует
Ускорение падения груза, определяется формулой
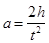 (14)
(14)
где h – высота, с которой падает груз, t – время, в течение которого падает груз с высоты h. Подставив (14) в (13), получим
Mz = m 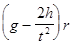 . (15)
. (15)
С таким же тангенциальным ускорением движутся все точки шкива, находящиеся на расстоянии r от оси вращения. Поэтому угловое ускорение шкива равно
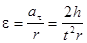 . (16)
. (16)
helpiks.org
