«Координаты. Координатная плоскость». 6-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Место урока в общей теме:

Общая тема «Положительные и отрицательные числа»

Это 1 урок по теме «Координаты»

• учащиеся знают определения положительных и отрицательных чисел
• учащиеся знают понятие координатной прямой
• умеют определять координаты точек координатной прямой
• умеют отмечать точки на координатной прямой по заданным координатам

1) образовательные:

• ввести понятие координат
• ввести понятие системы координат, координатных осей и координатной плоскости
• ввести понятие координат точки: абсциссы и ординаты
• научить определять координаты точек
• научить отмечать точки на координатной плоскости по заданным ее координатам
• закрепить полученные знания в ходе выполнения упражнений

2) развивающие:

• создать у учащихся положительную мотивацию к выполнению умственных и практических действий
• развитие коммуникативной и информационной компетентностей учащихся
• помочь развитию интереса у учащихся не только к содержанию, но и к процессу овладения знаниями
• развивать умение применять полученные знания в конкретной ситуации
• развивать логическое мышление, память, самостоятельность

3) воспитывающие:

1. воспитывать у учащихся чувство удовлетворения от возможности показать на уроке свои знания не только по математике, но и в других областях школьных знаний
2. развитие интереса к изучению математики
3. расширить умственный кругозор учащихся, помочь школьникам лучше понять роль математики в истории общества
4. воспитание дисциплинированности, организованности

Тип урока: урок усвоения новых знаний

В соответствие с типом урока выбраны следующие этапы урока

• организационный момент
• актуализация
• подготовка к активному и сознательному усвоению нового материала
• усвоение нового материала
• упражнения на понимание
• обобщение и систематизация знаний
• подведение итогов урока
• оглашение домашнего задания

I. Организационный момент.

Приветствие. Постановка пред учащимися долговременных целей по теме и задач по уроку.

II. Устная работа

Направлена на подготовку учащихся к активному и сознательному усвоению нового материала.

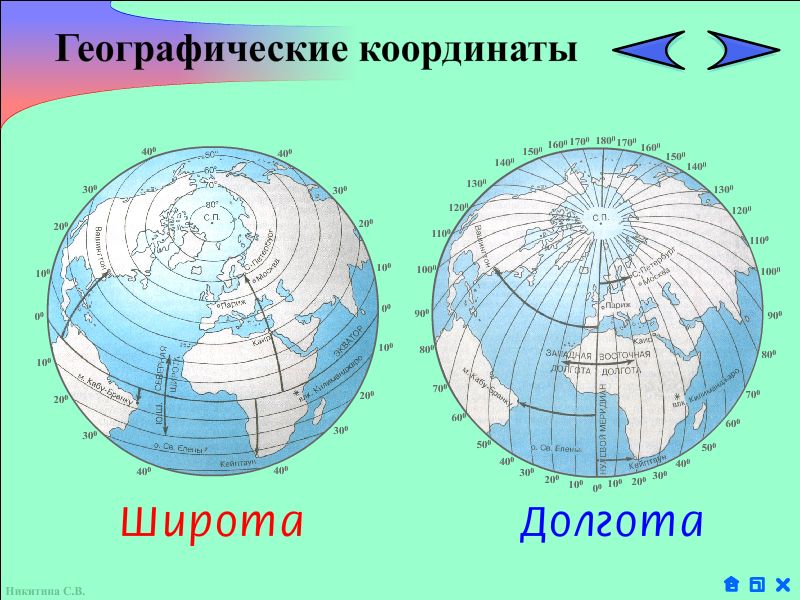
Координаты в жизненных ситуациях используются очень широко.

1. Привести примеры того, как в жизни используются координаты.





2. Предложить учащимся на основе рассмотренных примеров дать понятие координат.



III. Изучение нового материала.

1. Ввести понятие системы координат и координатной плоскости.

Учащимся предлагается рассмотреть рисунок и рассказать, что на нем изображено или ответить на вопросы.



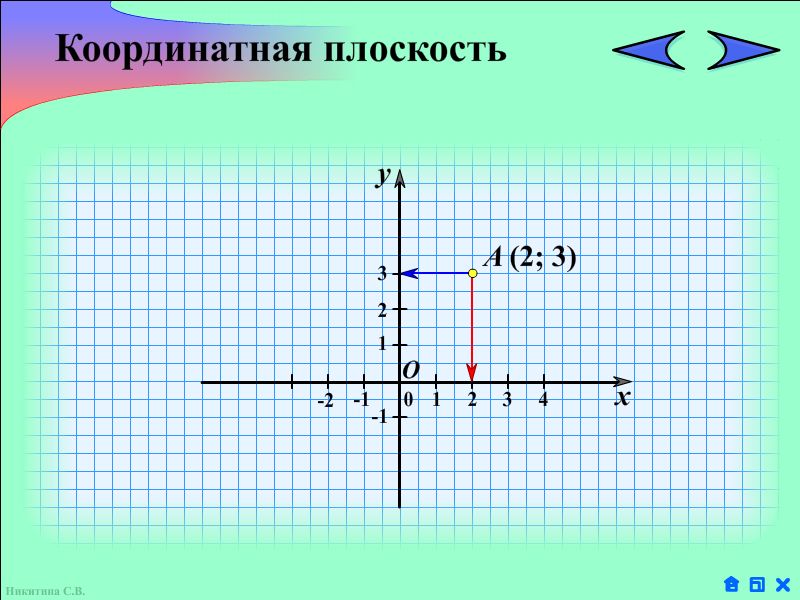
— Можно ли утверждать, что на рисунке изображены координатные прямые? Почему?

— Под каким углом расположены эти прямые к друг другу?

— Охарактеризовать точку пересечения этих прямых.

— Что напоминает запись 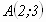? Чем она отличается от записи координаты точки на координатной прямой?

— Под каким углом из точки А проведены стрелки к координатным прямым 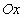и ?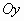

— Какая связь между точками координатных прямых, на которые указывают стрелки, и записью ?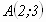

Выслушать ответы учащихся. Сделать выводы и ввести понятие системы координат, координатных осей, координатной плоскости, координат точки.



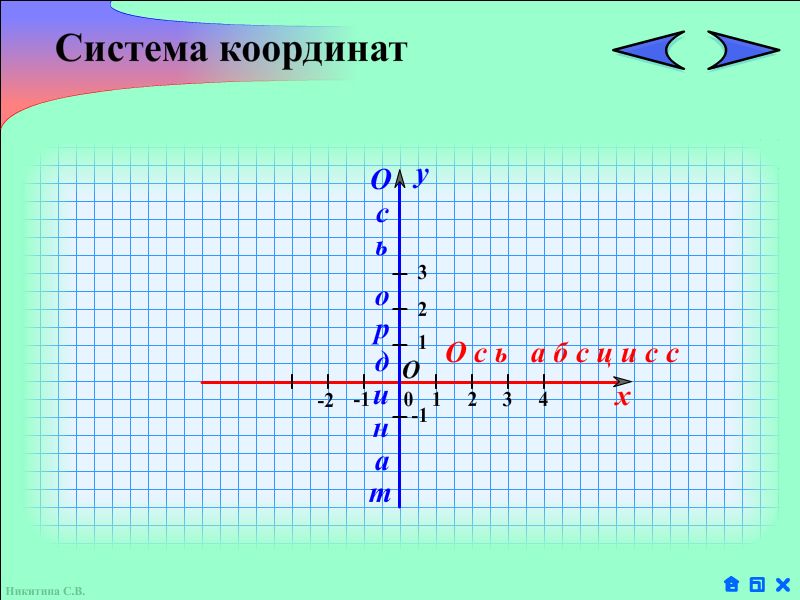
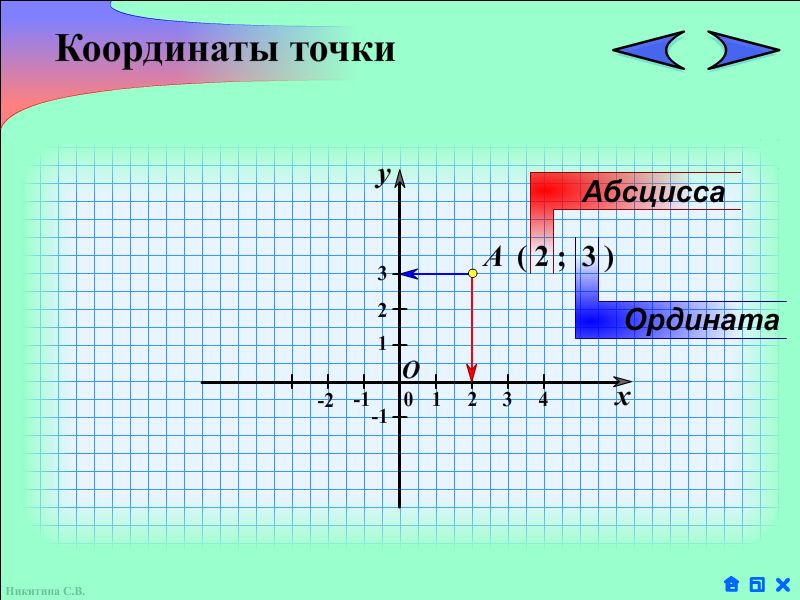
Координаты точки – пара чисел, по которым определяется положение точки на плоскости, где на первом месте стоит абсцисса, а на втором — ордината этой точки.

2. Ввести правило позволяющее определять координаты указанных точек.

Учащимся предлагается рассмотреть рисунок и определить координаты отмеченных точек.



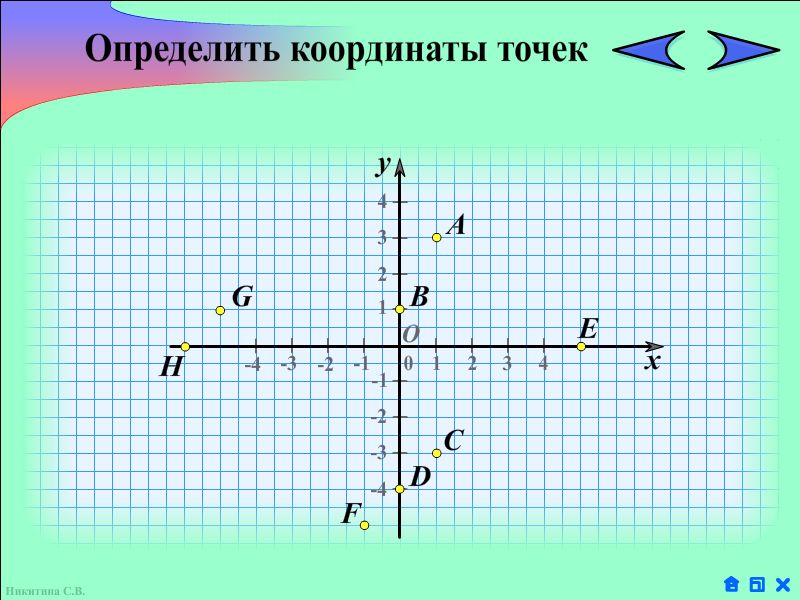
Попросить учащихся сформулировать правило, позволяющее определить координаты точки. Повторить его.

Чтобы определить координаты точки — надо из точки опустить перпендикуляры на координатные оси и определить, какому числу координатной оси соответствует основание перпендикуляра.

Для закрепления этого правила учащимся предлагается самостоятельно определить координаты отмеченных точек координатной плоскости, изображенных на экране. А затем проверить свое решение с тем, что на экране.



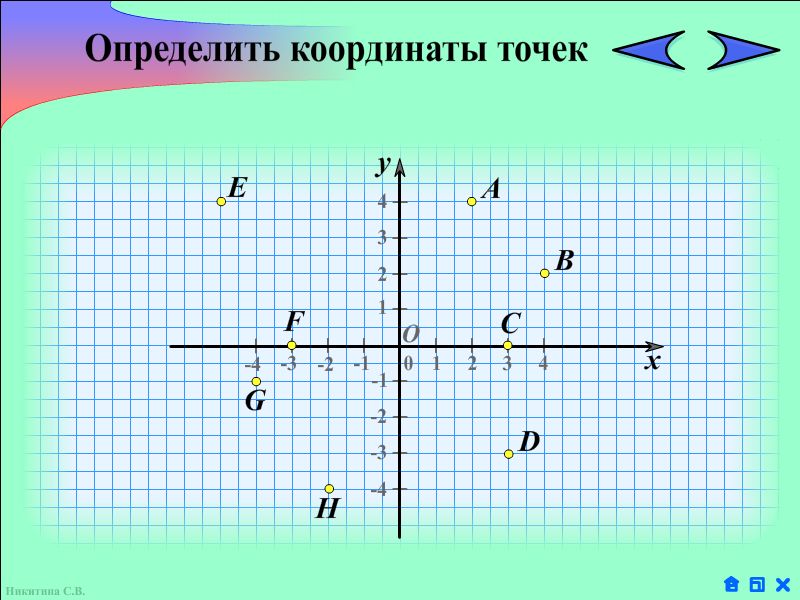
3. Определение положения точки на координатной плоскости по известным координатам.

Учащимся дается точка с заданными координатами. Задание – по известным координатам определить положение точки на координатной плоскости.



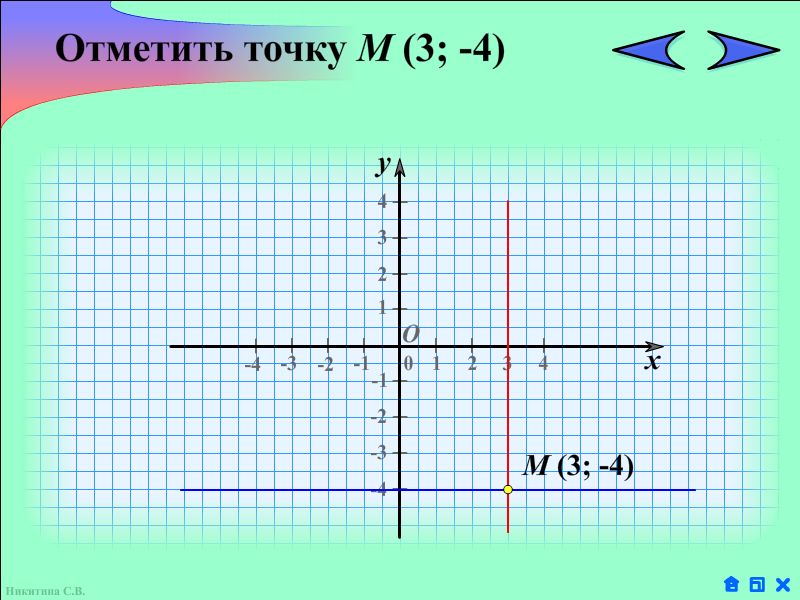
Сформулировать правило, позволяющее определять положение точки на координатной плоскости.

Чтобы определить положение точки на координатной плоскости – надо провести прямые, перпендикулярные осям, и найти точку их пересечения.

IV. Закрепление изученного материала.

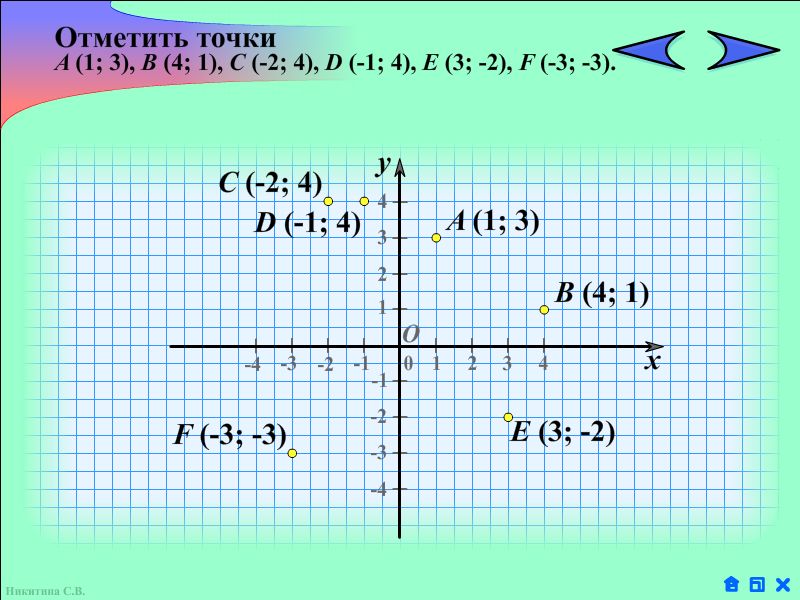
1. Учащимся предлагается построить координатную плоскость в тетрадях и отметить точки с указанными координатами, с последующей проверкой.



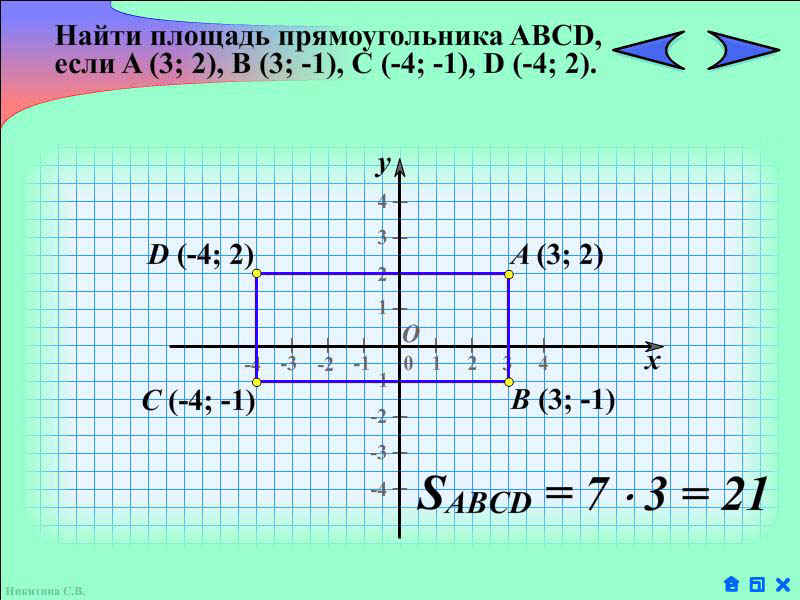
2. Резервное задание. Найти площадь прямоугольника, если известны координаты его вершин.



V. Подведение итогов урока. Выставление оценок.

— Что нового узнали сегодня на уроке? Чему научились?

— С какими понятиями познакомились?

— Какие правила сегодня изучили?

VI. Домашнее задание.

Практическое задание: начертить на листе бумаги в клетку систему координат, взяв единичные отрезок длиной 1 см (две тетрадные клетки). Отметить произвольно десять точек, не указывая их координаты.

xn--i1abbnckbmcl9fb.xn--p1ai

«Координатная плоскость». 6-й класс

Презентация к уроку

Цели урока:

Обучающие:

• ввести понятия координатная плоскость;
• изучить алгоритмы построения точки по заданным ее координатам и определять координаты точки, отмеченной на координатной плоскости;

Развивающие:

• использование для достижения поставленной задачи уже полученные знания;
• развивать умение обобщать, конкретизировать;

Воспитательные:

• расширение кругозора и развитие интереса к предмету, используя присущую математике красоту и увлекательность.

Планируемые результаты:

Предметные:

• знать что такое система координат, как называются координатные прямые, образующие эту систему, как называется точка пересечения этих прямых и пара чисел, определяющих положение точки на плоскости;
• уметь находить абсциссу и ординату точки на координатной плоскости и с их помощью строить точку.

Личностные:

• повышение мотивации к изучению предмета “математика”.

Метапредметные: в ходе урока учащиеся должны проявить следующие метапредметные умения:

• производить требуемую последовательность действий по инструкции, при необходимости уточнять формулировки задачи;
• сопоставлять и сравнивать информацию, находимую во внешних источниках (в том числе информацию, представленную в различных формах – в тексте и на модели, в учебнике и в форме интерактивного задания).

УУД:

• В процессе построения работы по теме урока я планировала вести работу над формированием у обучающихся следующих УУД
• формирование смысла учебной деятельности на основе развития познавательного интереса и учебных мотивов.

Познавательные:

• определять понятия, создавать обобщения, устанавливать аналогии;
• моделировать объект, а также преобразовывать полученную модель с целью выявления общих законов, определяющих данную предметную область.

Регулятивные:

• осуществлять контроль своей деятельности в процессе достижения результата в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
• корректировать свои действия в случае расхождения эталона, реального действия и его продукта.

Коммуникативные:

• уметь в коммуникации строить понятные для партнера высказывания, учитывающие, что он знает и видит, а что нет.

Место данного урока в теме:

• Данный урок третий по счету в теме “Координаты на плоскости”. Дети уже владеют знаниями о параллельных и перпендикулярных прямых, имеют представление о координатной прямой. Сегодня им предстояло открыть для себя новое понятие “координатная плоскость”.

Тип урока и его структура:

• Урок открытия нового знания. Исходя из этого, была выбрана следующая его структура:

Организационный этап.

1. Мотивация учебной деятельности учащихся.
2. Актуализация знаний.
3. Постановка цели и задач урока.
4. Первичное усвоение новых знаний.
5. Первичная проверка понимания
6. Первичное закрепление.
7. Рефлексия (подведение итогов занятия).

   Ход урока

   I. Организационный этап.

   II. Мотивация учебной деятельности учащихся.

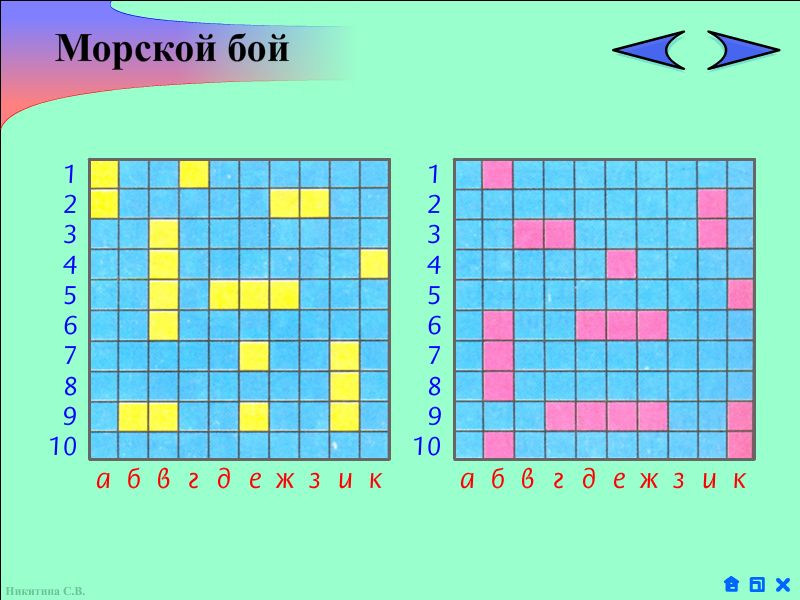
   Учитель: Ребята, кто из вас умеет играть в морской бой?

   Учитель: Давайте разработаем стратегию, как нам поразить 4х палубный корабль.

   Высказывают свои мнения, комментируют высказывания одноклассников.

   Ответ: (в, 3); (в, 4); (в, 5); (в, 6)

   Учитель: Каждая клетка на игровом поле определяется буквой и цифрой. Буквами помечены — горизонтали игрового поля, а цифрами — вертикали.

   На доске записать: (в, 3); (в, 4); (в, 5); (в, 6). Показать пересечение линий.

   Учитель: А в кино любите ходить?

   Учитель: Представим, что мы с вами в кинотеатре. Как вы находите свое место в кинотеатре по билету?

   Варианты ответов: Чтобы найти свое место в зале, сначала мы ищем свой ряд, затем своё место.

   42. Координатная плоскость. Правила

   Чтобы обозначить числами точное положение точки на плоскости,
   проводят две перпендикулярные координатные прямые — x и y ,
   которые пересекаются в начале отсчета — точке О (смотри рисунок).
   Эти прямые называют системой координат на плоскости, а точку О —
   началом координат. Плоскость, на которой выбрана система координат,
   называют координатной плоскостью.

   

   Пусть M — некоторая точка плоскости. Проведем через нее прямую MA ,
   перпендикулярную координатной прямой X , и прямую MB ,
   перпендикулярную координатной прямой Y . Так как точка A имеет
   координату 4, а точка B координату 3 , то положение точки M определяется
   парой чисел (4, 3) . Эту пару чисел называют координатами точки M .
   Число 4 называют абсциссой точки M , а число 3 — ординатой точки M .

   Координатную прямую X называют осью абсцисс,
   а координатную прямую Y — осью ординат.

   Точку M с абсциссой 4 и ординатой 3 обозначают так: M (4, 3) .
   На первом месте пишут абсциссу точки, а на втором ее ординату.

   Если переставить координаты местами, то получится другая точка
   N (3, 4) , которая тоже изображена на рисунке.

   Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

   Задачи на тему «Координатная плоскость»

   

   M (1, 2) ; M (1, 3) ; M (2, 1) ; Неверно. Не кликай на пустое поле. Неверно. Неверно.

   M (2, –1) ; M (1, 2) ; M ( –1, 2) ; Неверно. Не кликай на пустое поле. Неверно. Неверно.

   M ( –4, 3) ; M (3, –4) ; M (–4, 2) ; Неверно. Не кликай на пустое поле.

   M (4, 2) ; M (2, 4) ; M (2, 5) ; Неверно. Неверно. Неверно. Не кликай на пустое поле.

   M (3, 5) ; M (5, 3) ; M (4, 3) ; Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Нeвeрнo. Задание выполнено. Неверно.

   school-assistant.ru

   Координатная плоскость

   Этот урок посвящен изучению координатной плоскости. Мы рассмотрим, для чего используются координатные плоскости, разберем основные сведения. Также на уроке мы узнаем способ получения координатной плоскости из обычной и решим задачи, в которых научимся строить точки по заданным координатам и определять координаты точек, изображенных на координатной плоскости.

   Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 2. Треугольники. Координаты»

   Основные сведения о координатной плоскости

   Как известно, на каждом доме указаны его номер и название улицы – это адрес дома. На билете в любой зрительный зал написаны номер ряда и номер места – это адрес кресла. Для определения положения точки на глобусе надо знать долготу и широту – это адрес географической точки (географические координаты). Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.

   Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.

   Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх» (см. Рис. 1). На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают и называют осью ординат.

   Две перпендикулярные оси и с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал.

   

   Рис. 1. Координатная плоскость

   Координаты точки

   Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке 2 показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки , пересечение другой прямой с осью ординат – это координата точки . Сначала указывают координату , потом . Точка имеет координаты . Аналогично находим координаты точки , она имеет координаты (см. Рис. 2).

   

   Рис. 2. Определение координат точек на координатной плоскости

   Можно сделать все и в обратном порядке. То есть изобразить точку на плоскости по известным координатам.

   1. Построить точки по заданным координатам ,

   Для построения точки необходимо отложить число 2 на оси и провести перпендикулярную прямую; на оси откладываем число 5 и проводим перпендикулярную оси прямую (см. Рис. 3). На пересечении перпендикуляров получим точку с координатами .

   Для построения точки необходимо отложить на оси число 3 и провести перпендикулярную оси прямую; на оси откладываем число (–1) и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами . (см. Рис. 3).

   

   Рис. 3. Построение точек на координатной плоскости по заданным координатам

   2. Построить точки по заданным координатам ,

   Для построения точки необходимо отложить число 3 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).

   Для построения точки необходимо отложить число 2 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).

   

   Рис. 4. Построение точек на координатной плоскости по заданным координатам

   Таким образом, если нулю равна координата , то точка лежит на оси , а если нулю равна координата , то точка лежит на оси .

   1. Выписать координаты точек , , , (см. Рис. 5).

   2. Изобразить точки , , , , .

   

   Рис. 5. Иллюстрация к задаче

   1. Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты (см. Рис. 6).

   Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты .

   Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна (–2). Следовательно, точка имеет координаты .

   Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна –5. Следовательно, точка имеет координаты .

   

   Рис. 6. Иллюстрация к задаче

   2. Для построения точки откладываем число (–3) на оси и проводим перпендикулярную прямую; на оси откладываем число (–2) и проводим перпендикулярную оси прямую (см. Рис. 7). На пересечении перпендикуляров получим точку с координатами .

   Координата точки равна нулю, поэтому эта точка лежит на оси . Отложим на оси число 5 и получим точку с координатами .

   Для построения точки откладываем число 3 на оси и проводим перпендикулярную оси прямую; на оси откладываем число 4 и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами .

   Координата точки равна нулю, поэтому эта точка лежит на оси . Отложим на оси число (–4) и получим точку с координатами .

   Две координаты точки равны нулю, следовательно, эта точка лежит на оси и на оси , то есть является точкой пересечения двух осей (начало координат).

   

   Рис. 7. Иллюстрация к задаче

   Координатные четверти

   Координатные оси разбивают координатную плоскость на четыре части – четверти. Порядковые номера четвертей принято считать против часовой стрелки (см. Рис. 8).

   

   Рис. 8. Нумерация четвертей координатной плоскости

   Если точка имеет положительную координату и положительную координату , то она лежит в первой четверти.

   Если точка имеет отрицательную координату и положительную координату , то она лежит во второй четверти.

   Если точка имеет отрицательную координату и отрицательную координату , то она лежит в третьей четверти.

   Если точка имеет положительную координату и отрицательную координату , то она лежит в четвертой четверти.

   Например, у точки координата положительная, а координата отрицательная, следовательно, эта точка находится в четвертой четверти.

   Другие системы координат

   Чтобы присвоить точке числовой «адрес» (координаты), используются и другие системы координат.

   Причины использования различных систем координат:

   На этом уроке мы рассматривали прямоугольную систему координат на плоскости. Размерность такого пространства равна 2, то есть точка задавалась двумя координатами. Однако пространство может иметь другую размерность, например равную единице, когда точка может менять свое положение только в одном направлении (двигаться вперед-назад или вверх-вниз). В качестве примера можно привести движение автомобиля по ровной дороге или движение лифта. Для указания местоположения точки нужна только одна координата. Эта координата будет означать то расстояние, которое проехал автомобиль (см. Рис. 9), или этаж, на котором находится лифт (см. Рис. 10).

   

   Рис. 9. Координата в данном случае – это расстояние, на которое отъехал автомобиль

   

   Рис. 10. Координата в данном случае – этаж, на котором находится лифт

   В математике такая система координат представлена числовой или координатной осью. Чтобы из любой прямой получить координатную ось, необходимо отметить на прямой начало отсчета, масштаб и направление отсчета (см. Рис. 11). По одной координате можно однозначно понять, где находится точка.

   

   Рис. 11. Координатная ось

   Размерность пространства может быть равной трем (пространство, в котором мы живем, имеет три измерения). Для указания места положения точки в этом случае нужны три координаты. Например, если в высотном здании на каждом этаже находится кинотеатр, то для указания места в билете должны быть указаны три координаты – этаж, ряд, номер кресла. В математике такая система координат строится точно так же, как на плоскости, только добавляется третья ось (см. Рис. 12).

   

   Рис. 12 Декартова система координат в пространстве

   2. Другой метод задания координат точки (использование полярной системы координат на плоскости).

   Проводится ось , а для точки указывается расстояние от нуля до нее и угол, который образует отрезок с осью . Эти два числа и будут являться координатами точки (см. Рис. 13).

   

   Рис. 13. Полярная система координат на плоскости

   В трехмерном пространстве строятся аналогичные системы, например сферическая или цилиндрическая система координат.

   Таким образом, прямоугольная система координат широко применяется в математике, но не является единственной.

   Список литературы

   1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

   2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

   3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

   4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.

   5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.

   6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

   Дополнительные рекомендованные ссылки на ресурсы сети Интернет

   1. Интернет-сайт mathematics-repetition.com (Источник)

   2. Интернет-сайт youtube.com (Источник)

   3. Интернет-сайт exponenta.ru (Источник)

   Домашнее задание

   1. Вопросы в конце раздела 45 (§9), задание 1393, 1394, 1396, 1398 (стр. 245-246) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 (Источник)

   2. Выберите точки расположенные выше оси абсцисс: , , , , .

   3. В координатной плоскости построить следующие точки, соединяющие их последовательно с предыдущей точкой отрезком (получите определенный рисунок): , , , , , , , , , , , , , , , , , , , , , , , , , , , .

   Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

   interneturok.ru