закон Снеллиуса

Большой англо-русский и русско-английский словарь . 2001 .

Смотреть что такое «закон Снеллиуса» в других словарях:

закон Снеллиуса — закон синусов Закон, определяющий соотношение углов падения, отражения и преломления волн на границе раздела сред в зависимости от фазовых скоростей волн в этих средах. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего… … Справочник технического переводчика

Закон Снеллиуса — Преломление света на границе двух сред с различным показателем преломления … Википедия

Закон Снелла — Преломление света на границе двух сред с различным показателем преломления Преломление … Википедия

Закон преломления — Преломление света на границе двух сред с различным показателем преломления Закон Снелла (Снеллиуса) преломления света описывает преломление света на границе двух сред. Также применим и для описания преломления волн другой природы, например… … Википедия

закон преломления света Снеллиуса — Snelijaus šviesos lūžimo dėsnis statusas T sritis fizika atitikmenys: angl. Snell’s law of refraction vok. Snelliussches Brechungsgesetz, n rus. закон преломления света Снеллиуса, m pranc. loi de réfraction de Snell, f … Fizikos terminų žodynas

ЗВУК И АКУСТИКА — Звук это колебания, т.е. периодическое механическое возмущение в упругих средах газообразных, жидких и твердых. Такое возмущение, представляющее собой некоторое физическое изменение в среде (например, изменение плотности или давления, смещение… … Энциклопедия Кольера

Снелл, Виллеброрд — Виллеброрд Снелл ван Ройен Willebrord Snel van Royen … Википедия

ОПТИКА — раздел физики, в котором рассматриваются все явления, связанные со светом, включая инфракрасное и ультрафиолетовое излучение (см. также ФОТОМЕТРИЯ; ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ). ГЕОМЕТРИЧЕСКАЯ ОПТИКА Геометрическая оптика основывается на… … Энциклопедия Кольера

Закон Снеллиуса

Закон Снеллиуса (также Снелля или Снелла) преломления света описывает преломление света на границе двух прозрачных сред. Также применим и для описания преломления волн другой природы, например звуковых.

• Теоретическое объяснение закона Снеллиуса — см. в статье Преломление.

Закон был открыт в начале XVII века голландским математиком Виллебрордом Снеллиусом [1] .

Угол падения света на поверхность связан с углом преломления соотношением



• — показатель преломления среды, из которой свет падает на границу раздела;
• — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;
• — показатель преломления среды, в которую свет попадает, пройдя границу раздела;
• — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.

Если n_2\,» border=»0″ />, имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред)

• Следует заметить, что в случае анизотропных сред (например, кристаллов с низкой симметрией или механически деформированных твердых тел) преломление подчиняется несколько более сложному закону. При этом возможна зависимость направления преломленного луча не только от направления падающего, но и от его поляризации (см. двойное лучепреломление).
• Также следует заметить, что закон Снеллиуса не описывает соотношение интенсивностей и поляризаций падающего, преломленного и отраженного лучей.
• Закон Снеллиуса хорошо определен для случая «геометрической оптики», то есть в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря работает в рамках приближенного описания, каковым и является геометрическая оптика.

Векторная формула

Пусть и лучевые векторы падающего и преломленного световых лучей, то есть векторы, указывающие направления лучей и имеющие длины и , а единичный нормальный вектор к преломляющей поверхности в точке преломления. Тогда



Примечания

1. ↑ Снеллиус — латинизированная форма оригинальной фамилии Снелл, передающейся чаще как Снелль

Wikimedia Foundation . 2010 .

Смотреть что такое «Закон Снеллиуса» в других словарях:

Закон Снелиуса — Преломление света на границе двух сред с различным показателем преломления Закон Снелла (Снеллиуса) преломления света описывает преломление света на границе двух сред. Также применим и для описания преломления волн другой природы, например… … Википедия

Закон преломления света — Преломление света на границе двух сред с различным показателем преломления Закон Снелла (Снеллиуса) преломления света описывает преломление света на границе двух сред. Также применим и для описания преломления волн другой природы, например… … Википедия

ФИЗИКА — (от древнегреч. physis природа). Древние называли физикой любое исследование окружающего мира и явлений природы. Такое понимание термина физика сохранилось до конца 17 в. Позднее появился ряд специальных дисциплин: химия, исследующая свойства… … Энциклопедия Кольера

dic.academic.ru

Закон — снеллиус

Закон Снеллиуса, полное внутреннее отражение и дисперсия света являются ключевыми вопросами для дальнейшего развития курса. Решение задач и лабораторные работы должны закреплять и углублять знакомство с этими вопросами.
Закон Снеллиуса помогает определять лучевые траектории и времена вступления, а также находить положение отражающего горизонта по наблюдаемым временам вступлений, но он не дает информации об амплитудах отраженных и проходящих волн.
Пучки световых лучей входят в призму слева снизу. Два крайних пучка, входящих в призму ближе к ее правой грани, испытывают полное внутреннее отражение на горизонтальной границе стекла с воздухом, остальные четыре пучка частично отражаются и частично преломляются на той же поверхности. Применяя закон Снеллиуса ко всем случаям без разбора, мы можем очень скоро попасть впросак.
Однако закон Снеллиуса не учитывает изменения, происходящие в веществе под воздействием излучения ( они для луча света незначительны), а закон Максвелла Cic / / ejJ не раскрывает превращений параметров электрического сопротивления электролитов под воздействием ЭДС постоянного тока.
Согласно закону Снеллиуса, он соответствует углу полного внутреннего отражения. Его определяют с помощью рефрактометра.
Мы получили закон Снеллиуса, который соблюдается не только для звука, но и для любых волновых процессов.
Дважды применяя закон Снеллиуса (2.11.8), легко показать, что угловое отклонение луча после попадания из вакуума на кромку диэлектрического клина с показателем преломления п и углом тг / 2 дается выражением в 0 — arcsin ( 1 sin20 — л2) 172, где 0 — угол падения.
Векторная диаграмма, поясняющая то, что происходит на Н. З. Это и есть закон Снеллиуса, причем показатель преломления должен быть равен VH / VB. Пользуясь значениями скоростей VB n VH, измеренными стробоскопически, и непосредственно измеренными углами, мы можем произвести перекрестную проверку нашей модели.
Схема движения световых лучей в рефрактометре. При этом согласно закону Снеллиуса отношение синуса угла падения ( независимо от величины этого угла) к синусу угла преломления есть для данных двух сред постоянная величина, как раз и называемая показателем преломления.
В соответствии с законом Снеллиуса (1.1) на границе раздела сред происходит преломление волн, вследствие чего изменяется угол между интерферирующими пучками.
Выражение (63.2) называют законом Снеллиуса, хотя Снеллиус формулировал его не через синусы, а через косекансы.
Волновые векторы при преломлении и отражении на плоской поверхности.
Второе соотношение называется законом Снеллиуса.
Это выражение известно как закон Снеллиуса. На рис. 3.8 АО — направление падающего пучка света, а ОВ — отраженного пучка, так что угол падения i равен углу отражения /, но противоположен ему по знаку.
На рис. 5.46 второй закон Снеллиуса поясняется при помощи семейства кривых ( ф) для случая двух идеальных диэлектриков; при этом п Ув1 и И2 Уб2 вещественны. Биссектриса выделяет два класса процессов преломления.
Из геометрических соотношений вытекает закон Снеллиуса. При таком изменении количества движения корпускулы должны двигаться в воде быстрее, чем в воздухе.
Волновые векторы при преломлении и отражении на плоской поверхности. J Второе соотношение называется законом Снеллиуса.
Схема трансформации ( а и схема к выводу закона Снел-лиуса ( б при падении ультразвуковой волны на границу раздела двух твердых сред. Это выражение часто называют законом Снеллиуса или законом синусов.
Соотношение (4.1) иногда называют законом Снеллиуса.
Работа Кеплера была аналогична установлению закона Снеллиуса. Однако в случае Солнечной системы совокупность полученных Браге данных была неизмеримо сложнее, и установить среди них закономерность было делом гораздо более трудным и великим.
Второе условие (7.56) при учете закона Снеллиуса дублирует третье условие.
Это выражение представляет собой обобщение закона Снеллиуса для сред со сферически-симметричным профилем показателя преломления. Оно известно также как теорема Боугера, которую можно интерпретировать как закон сохранения углового момента фотонов, движущихся через среду.
Преломление света изотропными телами подчиняется закону Снеллиуса — Декарта.
Трансформация ультразвуковой волны, падающей на границу раздела. Значения критических углов можно найти из закона Снеллиуса, подставив в выражение ( 68) sinae 1 и sincc 1, что соответствует а.

Для света подобное преломление количественно описывается законом Снеллиуса. Напрашивается следующий вопрос: применим ли закон Снел-лиуса также и к волнам, например к волнам в кювете, проходящим из одной среды в другую.
При углах падения, превышающих в, закон Снеллиуса не может выполняться ( при использовании вещественных значений углов), так как sin 62 не может превышать единицу, и происходит полное внутреннее отражение.
Хотя и полезно делать упор на формулировку закона Снеллиуса через отношение полухорд, однако не следует игнорировать и его выражение через синусы.
Показать, что волны на воде подчиняются закону Снеллиуса.
Это выражение (2.8) обычно называется в оптике законом Снеллиуса. Хорошо известно, что законы отражения и преломления световых волн служат основой геометрической оптики. Мы видим, что в электромагнитной теории света эти законы получаются в самом общем виде без введения каких-либо специальных предположений, как следствие записанных выше граничных условий для уравнений Максвелла. Они справедливы для электромагнитных волн в любом диапазоне частот.
Даже если учащиеся хорошо знакомы с синусами, закон Снеллиуса лучше сначала вводить с помощью полухорд.
Если среда состоит из ряда параллельных слоев, закон Снеллиуса требует, чтобы величина р имела одно и то же значение повсюду для всех отраженных и преломленных лучей, образовавшихся из данного падающего луча.
Этот закон формально можно рассматривать как частный случай закона Снеллиуса, а именно тот, когда показатель преломления п равен единице. В технической практике обычно пользуются лишь плоскими и вогнутыми ( сферическими, параболическими) зеркалами. Выпуклые зеркала не имеют действительного фокуса и дают лишь мнимые изображения.
В приводимом выводе не используется ничего, кроме закона Снеллиуса, геометрии и радианной меры углов.
Условие непрерывности нормальной составляющей D в совокупности с законом Снеллиуса приводит к условию, повторяющему второе из этих соотношений.
Учащимся нужно теперь разъяснить, что для белого света закон Снеллиуса ( при постоянном п) является лишь приближением. Но при этом необходимо подчеркнуть, что для одноцветного луча закон Снеллиуса оправдывается точно.
Что же касается рассмотренного эффекта, то оказывается, что закон Снеллиуса выполняется лишь при отражении от неподвижного зеркала. Если же зеркало движется с достаточно большой скоростью, то угол падения перестает быть равным углу отражения.
Рассматриваемый материал важен главным образом потому, что он вводит закон Снеллиуса. Его значение, однако, заключается также в том, что он иллюстрирует обычные в науке поиски закономерностей, способных обобщать экспериментальные данные. При выполнении опыта II.3, включая графическую обработку данных, до задания на дом раздела 13.3 учащиеся подойдут к самостоятельному открытию закона Снеллиуса настолько близко, насколько это позволит отведенное время.
Если есть возможность найти угол преломления в призме, то закон Снеллиуса позволит сразу найти и угол падения.

Соотношение sini / sin rconst есть не что иное, как закон Снеллиуса, но на этот раз выведенный для волн.
Это уравнение называется теоремой Клэро, которую можно рассматривать как обобщение закона Снеллиуса [ см. также теорему Боу-гера (2.13.40) ] применительно к однородной среде.
При дальнейшем увеличении угла падения ( фФ), как следует из второго закона Снеллиуса, sindl.
Ответ: Угол падения равен углу отражения: a / 3 известный в оптике закон Снеллиуса.
Угол В2 называется углом преломления, а (2.103) выражает закон преломления, известный также как закон Снеллиуса. Углы обычно измеряют между лучами и нормалями к поверхности, но в изотропных средах они совпадают с углами между поверхностью и волновыми фронтами. Законы отражения и преломления можно объединить в одно общее утверждение: па некоторой границе раздела величина р ( sinO /) / l / / имеет одно и то же значение для падающих, отраженных и преломленных волн.
Телескопическая система, состоящая из двух цилиндрических электростатических линз. Уравнение ( 9, 80) показывает, что отклонение пучка в телескопической системе подчиняется закону Снеллиуса.
Ко времени изучения этого раздела большинство учащихся уже способно строить ход лучей в призме с помощью закона Снеллиуса. Однако некоторые из них еще не приобрели интуитивного ощущения того, отклоняется ли свет призмой, вверх или вниз. В таком случае требуется прямое разъяснение, что луч света отклоняется в ту сторону, где стекло толще. Это разъяснение нужно многократно повторять. Но даже и после ознакомления с этим мнемоническим правилом учащимся полезно изредка применять закон Снеллиуса на каждой преломляющей грани призмы.
Для произвольного угла падения коэффициенты отражения Др и Rs легко вычисляются с помощью выражений (3.8.2) и закона Снеллиуса.
Из опытов, в которых свет идет из других веществ в воздух, вытекает заключение, что закон Снеллиуса оправдывается одинаково точно при входе света в вещество и выходе из него.
Посмотрим теперь, какие следствия относительно скорости света в пустоте и в среде вытекают из корпускулярного вывода закона Снеллиуса.
При тех положениях точек А и В, которые показаны на рис. 201, путь 1 соответствует закону Снеллиуса. Путь 2 проходит вблизи действительного пути света 1, определяемого законом Снеллиуса, но составляет с нормалью угол 45 в воздухе и угол 30 в плотной среде.
Прохождение света из стекла в воду через слой воздуха. Может показаться, что переход от формулы sin i / sin rconst к формуле ni sin91n2 sin92 существенно изменяет закон Снеллиуса. Однако это неверно, в чем легко убедиться после небольшой перестановки членов последнего равенства.
Опыт, предложенный и поставленный Фуко ( 1850) был основан на сравнении формул (137.1) и (137.4) для выражения закона Снеллиуса. Не учитывая принципиальной разницы между скоростями с и с, с одной стороны, и v и о — с другой, Фуко полагал, что для решения вопроса о природе света, нужно непосредственно измерить скорость света в какой-нибудь среде, а не судить о ней на основе показателя преломления. Если эта скорость окажется меньше скорости света в пустоте — верна волновая теория, в противном случае — верна корпускулярная ( в ньютоновом смысле) теория.

www.ai08.org

Угол преломления луча при прохождении границы между двумя средами зависит от соотношения коэффициентов преломления этих сред.

Теория относительности заставила нас усвоить, что ничто не движется быстрее света, но при этом в такой формулировке имеется одна маленькая хитрость, о которой часто забывают. Теоретики, говоря «скорость света», имеют в виду скорость света в вакууме, которую принято обозначать латинской буквой с, и для них это настолько самоочевидно, что дополнение «в вакууме» они обычно не озвучивают. А ведь при распространении света в прозрачной среде, например, воде или стекле, он движется значительно медленнее скорости с из-за непрерывного взаимодействия с атомами материальной среды.

Так что же происходит с фронтом световой волны при ее прохождении через границу двух прозрачных сред? Ответ на это дает закон Снеллиуса (или «закон Снелля», если следовать не латинскому, а голландскому написанию. — Прим. переводчика), названный по имени голландского естествоиспытателя Виллеброрда Снеллиуса, впервые сформулировавшего эту закономерность. Важнейший пример такого преломления мы наблюдаем при попадании светового луча из воздуха в стекло и затем снова в воздух — а именно это происходит (причем зачастую неоднократно) в любом оптическом приборе, будь то сложнейшее лабораторное оборудование или банальная пара очков. Представьте себе туристов, идущих гуськом по диагонали через квадратное поле, посередине которого, параллельно двум его сторонам, проходит граница, после которой начинается болото. Понятно, что по чистому полю туристы могут идти быстрее, а по болотной жиже — медленнее. И вот, когда первые туристы доходят до края болота и начинают вязнуть в грязи, скорость их продвижения падает, и они, как нормальные люди, отклоняются от курса, чтобы поскорее добраться до противоположного края болота, в то время как идущие следом движутся с прежней скоростью и в прежнем направлении. По мере залезания в болото всё новых туристов они также сбрасывают скорость и начинают срезать угол. В итоге с высоты птичьего полета процессия туристов выглядит преломленной — по полю она идет в одном направлении, а по болоту — в другом. То же и со световым лучом: если при пересечении границы двух сред скорость света во второй среде ниже, чем скорость света в первой среде, луч отклоняется в сторону нормали (линии, перпендикулярной границе). Если же во второй среде скорость распространения света выше (как, например, при переходе света из стекла в воздух), луч, напротив, отклонится от нормали на больший угол (туристы ускорят шаг и спрямят направление).

Отношение скорости света в вакууме к скорости света в среде называется коэффициентом преломления среды. Так, коэффициент преломления стекла равен примерно 1,5 (зависит от сорта стекла), то есть, свет в стекле замедляется примерно на треть по сравнению со скоростью его распространения в вакууме. У каждого прозрачного материала — собственный коэффициент преломления (совпадения, конечно же, возможны, но они ни о чем не говорят).

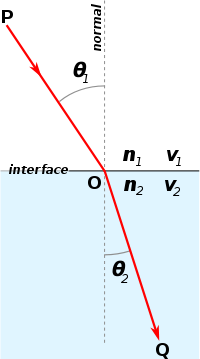
Закон Снеллиуса устанавливает числовое соотношение между углами падения и преломления луча при переходе из одной среды в другую. Если θ₁ и θ₂ — углы, соответственно, падения и преломления относительно нормали (см. рисунок) при переходе луча из одной среды в другую, а n₁ и n₂ — коэффициенты преломления этих сред, то имеет место соотношение:

Смысл этого закона в том, что если известны коэффициенты преломления света в двух граничащих средах и угол падения луча, можно рассчитать, насколько отклонится луч после пересечения границы между средами.

Доводилось ли вам когда-либо стоять у бортика бассейна и удивляться, отчего это у вашей подруги, стоящей по пояс в воде, ноги кажутся непропорционально короткими? А всё дело в том, что световые лучи, которые вы воспринимаете и которые доносят до вас зрительный образ, выйдя из воды и попав в воздух, преломились — и достигают ваших глаз под более тупым углом, чем если бы бассейн стоял без воды. Мозг же верит глазам, и вам кажется, что ступни вашей подруги ближе, чем они есть на самом деле.

elementy.ru

Закон Снеллиуса (Закон преломления)

На мой взгляд, начало оптического проектирования было положено в 1621 году. В этом году Снеллиус сформулировал закон преломления, который гласит, что если угол между падающим лучом и нормалью поверхности проведенной к точке падения, названный углом падения, обозначить через ; и если угол преломления – угол между преломленным углом и нормалью – обозначить через ; тогда взаимосвязь этих углов будет определяться следующим выражением

Кроме того, закон Снеллиуса полагает, что падающий луч, преломленный луч и нормаль проведенная к точке падения находятся в одной плоскости (рисунок 1). Величины и – коэффициенты преломления двух материалов. В то время как выражение (1.1) может быть принято за определение коэффициента преломления материала, более фундаментально эта величина определяется как

где – скорость света в вакууме, а – скорость света в веществе.

Рисунок 1.2 – Закон Снеллиуса (закон преломления)

Поскольку для любой поверхности отношение коэффициентов преломления определяет угол преломленного луча, то удобно записать

так что закон Снеллиуса упростится до следующего выражения

В случае отражения (рисунок 1.3), угол отраженного луча равен углу падения. Эти два угла имеют противоположный знак, согласно правило знаков для углов при распространении лучей. Следовательно, закон отражения можно представить как

При разработке оптики, отражение обычно принимают за частный случай преломления со следующими условиями

или (1.6)

Этот метод очень полезен при разработке центрированных систем с отражающими поверхностями, т.к. формула для преломления может быть применена к отражающей поверхности практически без изменений при условии, что мы примем на вооружение правило, что коэффициент преломления изменяет свой знак после каждого отражения. После четного числа отражений, когда лучи распространяются в том же направлении, в котором они распространялись первоначально, коэффициент преломления будет положительным; после нечетного числа отражений коэффициенту преломления будет присвоено отрицательное значение.

Рисунок 1.3 – Закон отражения

В случае сложных децентрированных систем – систем с наличием нескольких поворотных зеркал – это соглашение (условие, что после отражения коэффициент преломления остается прежним, но со знаком минус) может сбить с толку. Возможно в этом случае более удобно рассматривать отражения как отдельный случай, оставляя все коэффициенты преломления положительными.

optoelectrosys.ru