6.3. Закон исключенного третьего

Впервые этот закон сформулировал Аристотель, хотя он был известен задолго до него и в логических учениях Древнего Востока, и в школах риторики Античной Греции.

Начиная с Аристотеля существует традиция давать закону исключенного третьего разные интерпретации, наиболее важной из которых является, несомненно, логическая. Она требует, чтобы из двух противоречащих суждений одно было истинным, а другое – ложным. Другое истолкование, называемое онтологическим, переносит логический закон на реальный мир, т.е. постулирует например, что свойство должно либо принадлежать, либо не принадлежать предмету, или же объект либо существует в мире, либо не существует. Ясно, однако, что этот закон, как и другие логические законы, абстрагируется от всей сложности и противоречивости реального мира и поэтому не может быть полностью, без соответствующих уточнений перенесен на объективный мир, его свойства и отношения. Точно так же методологическое требование, чтобы в процессе исследования было установлено, является ли объект (система суждений, гипотез или теория) истинным либо ложным, представляет собой перенос логического принципа на область учения о методах познания и критериев их истинности. Иногда даже под закон исключенного третьего подводится психологическая база, но подобные истолкования закона не вытекают из самого закона, который является логически необходимой, общезначимой истиной, относящейся непосредственно к двум контрадикторным суждениям. Закон просто требует, чтобы из таких суждений одно было истинным, а другое ложным; никакой третьей возможности не допускается. Отсюда легко находится формула для символического выражения закона. Суждения (или высказывания) в ней должны отрицать друг друга, и кроме того, они должны быть связаны строгой (сильной) дизъюнкцией, словесно выражаемой грамматическими союзами «либо, либо», т.е. если мы обозначим одно суждение через Р, а его отрицание – ¬ Р, тогда формула будет такой:

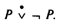
Вопрос о применении закона исключенного третьего еще со времени Аристотеля вызывал споры. Сам философ считал его применимым лишь для характеристики настоящих и прошлых событий, так как человек может определить истинность и ложность только таких событий. Вопрос об истинности будущих событий остается неопределенным. По-видимому, Аристотель и его предшественники вывели этот закон из наблюдения свойств конечных множеств событий. Когда математики обратились к исследованию свойств бесконечных множеств, то вынуждены были признать, что если бесконечность рассматривается как неограниченный процесс построения каких-либо объектов, например, чисел натурального ряда 1, 2, 3. то к ним принцип исключенного третьего оказывается неприменимым. В самом деле, суждение «В данном бесконечном ряду не существует объекта со свойством Р, т.е. Р(х)» было бы истинным только тогда, когда существовала бы возможность проверить бесконечный ряд целиком. Но именно подобным образом рассуждают сторонники классической (или теоретико-множественной) математики, когда рассматривают бесконечное множество по аналогии с конечными множествами, т.е. как завершенное, актуальное множество. С такой точки зрения натуральный ряд чисел представляется как уже заданный, готовый, а не возникающий в процессе прибавления единицы к предшествующему числу.

Для чего понадобилась эта идеализация? Оказывается для того, чтобы сохранить все законы аристотелевской (классической) логики и для бесконечных множеств. Однако подобный упрощенный подход привел в дальнейшем к парадоксам теории множеств, в связи с чем противники классиков – интуиционисты и конструктивисты – отказались от применения закона исключенного третьего. На этой основе возникла особая – конструктивная логика, отличающаяся от классической тем, что в ней не используется закон исключенного третьего.

Трудности с применением данного закона возникли также в квантовой механике, изучающей законы движения микрочастиц материи, где потребовалось ввести закон исключенного четвертого.

Приведенные примеры из современной науки ясно показывают, что прежде чем применить закон исключенного третьего к конкретным областям научного знания или даже к повседневной практике, необходимо убедиться, подходит ли он для данного случая, не вносит ли путаницу и не приводит ли к ошибочным выводам.

Следовательно, важно разобраться, как соотносятся между собой законы противоречия и исключенного третьего, какую роль они играют в логическом анализе рассуждений в речи или тексте. Заметим, что принцип противоречия имеет более общий характер, ибо устанавливает, что два противоречащих суждения не могут быть одновременно истинными, но не указывает что одно из них должно быть истинным, а другое ложным. Поэтому он применяется и к контрарным, и контрадикторным суждениям. Как известно, общеутвердительные и общеотрицательные суждения являются контрарными, т.е. допускают существование суждений, занимающих промежуточное положение между ними. Например, суждения «все экстрасенсы приносят пользу людям» и «ни один экстрасенс не приносит пользу» предполагают существование частноутвердительного суждения «некоторые экстрасенсы приносят пользу людям». Итак, когда мы имеем дело с противоречием, то в результате его анализа всегда можно выделить некоторое суждение, характеризующее промежуточное состояние, степень свойства, признака и т.п. Другими словами, члены такого противоречия не только отрицают друг друга, но и предполагают существование третьей возможности.

Контрадикторные суждения исключают третью возможность: они допускают выбор только между двумя возможностями. Нередко подобные суждения представляются в виде определенной альтернативы. Альтернатива требует выбора между двумя контрадикторными суждениями: либо вы считаете истиной одно мнение (гипотезу или утверждение) либо другое, и ничего, кроме этих альтернатив не допускается. Такой подход характерен для постановки проблем в научном познании или решения вопросов в практической деятельности. В этих случаях рассуждают по принципу «либо – либо» и тем самым заставляют исследовать или решать либо одну проблему или задачу, либо другую. Но отсюда, конечно, отнюдь не следует, что с самого начала исследования или решения выбирается истинное направление или решение, а просто-напросто постулируется возможность выбора между двумя возможностями. Выбор может оказаться неверным и решение проблемы или задачи отрицательным, но такой отрицательный результат оказывается небесполезными, ибо в соответствии с требованием закона исключенного третьего правильное решение следует искать путем реализации второй возможности.

Косвенные доказательства, основанные на применении принципа исключенного третьего, как мы видели в предыдущих главах, также строятся по принципу альтернативы. Предполагая тезис ложным, рассуждая от противного, выводят из него следствия, которые противоречат истинным или доказанным утверждениям. Поскольку из двух взаимоисключающих суждений только одно должно быть истинным, то ложность предполагаемого тезиса отрицается и тем самым доказывается его истинность.

Таким образом, если принцип непротиворечия требует анализа возникшего противоречия и его устранения, то принцип исключенного третьего идет дальше, ибо устраняет возможность выбора какого-то третьего суждения, кроме тех суждений, которые являются членами данной альтернативы. Именно поэтому последний закон называют также принципом альтернативы, что отображается в логической структуре самого закона. Если в законе непротиворечия отрицается конъюнкция противоречащих суждений, то в законе исключенного третьего отвергается существование третьей возможности наряду с двумя альтернативными:

www.bibliotekar.ru

Закон исключенного третьего

Формула закона исключённого третьего: из двух противоречащих мыслей одна является истинной,

а вторая ложной; третьего не дано (закону исключённого третьего подчиняются только противоречащие мысли).

Противоречащие мысли (отрицающие друг друга) – парные, их всегда только две. Третьей мысли не может быть. Например, истинно «он успел на поезд» либо истинно «он не успел на поезд», попытка найти истину в третьем высказывании «он недоуспел на поезд» оказывается безуспешной (в примере говорилось об одном и том же человеке, об одном и том же поезде и об одном и том же времени).

Следствие, вытекающее из закона исключённого третьего: если одна противоречащая мысль ложна, то вторая обязательно истинна. Например, если мысль «Зюганов голосовал за Путина» ложна, то противоречащая мысль «Зюганов не голосовал за Путина» обязательно истинна.

Если перед нами противоречащие мысли, то из ложности одной следует истинность другой и, наоборот, из истинности одного утверждения следует ложность другого.

Если утверждение-тезис противоречит фактам или истине (если чёрное выдают за белое), возникает логическая ошибка «ложный тезис».

Пример. «Экономика России за годы демократических реформ совершила мощный рывок в развитии, доказав фактами преимущество перед экономикой СССР».

Теория, в которой нет противоречий, называется непротиворечивой. Только с помощью таких теорий делаются правильные выводы. Отсутствие противоречий говорит о правильности рассуждений.

А противоречивая теория – чушь собачья.

Противоречия обычны для пустомель.

— Это ваше убеждение?

Пример 2. (противоречивые утверждения Ельцина Б. Н.)

«1995 год мы начали лучше, чем в прошлом году. В половине отраслей промышленности отмечается рост производства» (18.03.1995. «Российская газета»).

«О подъёме отечественного производства. Мы об этом в 1995 – 1996 годах и не мечтали (1997. Радиообращение).

Сперва старый хрен говорит, что рост производства был в 1995 году, потом утверждает, что роста производства не было в 1995 году. Противоречащий себе политик — посмешище.

ВНИМАНИЕ! Закон исключённого третьего работает при выполнении закона тождества (при наличии однозначного смысла в утверждениях).

Если мысли сформулировать не по закону тождества, получится ерунда на постном масле.

Пример 1. «Дух – зеленый» или «Дух – не зеленый»? Какое из двух утверждений истинно?

Ответ прост. В обоих утверждениях нет однозначного смысла. Оба утверждения бессмысленные. Истиной тут и не пахнет.

— Он успел на поезд.

— Он не успел на поезд.

Если говорят о разных людях, или о разных поездах, или о разном времени, то перед нами не противоречащие мысли (отрицающие друг друга), а мысли совместимые (ситуация, выраженная поговоркой «В огороде бузина, а в Киеве дядька»).

Совместимые мысли не отрицают друг друга.

Дмитрий Мезенцев (координатор проекта «Русское Общество Добродействия») 2011 г.

www.ob-dobr.ru

Закон исключения 3

3. ЗАКОН ИСКЛЮЧЁННОГО ТРЕТЬЕГО

Закон исключённого третьего, как и закон противоречия, устанавливает связь между противоречащими друг другу высказываниями. Он утверждает: из двух противоречащих высказываний одно является истинным.

А или не-А. Например: «Аристотель умер в 322 г. до н.э. или он не умер в этом году», «Личинки мух имеют голову или не имеют её» и т.п. Само название закона выражает его смысл: дело обстоит так, как говорится в рассматриваемом высказывании, или так, как говорится в его отрицании, и никакой третьей возможности нет.

Как выразил эту мысль Аристотель: «…Не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать».

Человек говорит прозой или не говорит прозой, кто-то рыдает’ или не рыдает, собака выполняет команду или не выполняет её и т.п. — других вариантов не существует. Мы можем не знать, противоречива некоторая теория или нет, но на основе закона исключённого третьего ещё до начала исследования мы вправе заявить: она или непротиворечива или противоречива.

Этот закон с иронией обыгрывается в художественной литературе. Причина иронии понятна: сказать «Нечто есть или его нет», значит, ровным счётом ничего не сказать, и смешно, если кто-то этого не знает.

В «Мещанине во дворянстве» Ж.-Б.Мольера есть такой диалог:

Г-н Журден. …А теперь я должен открыть вам секрет. Я влюблён в одну великосветскую даму, и мне хотелось бы, чтобы вы помогли написать ей записочку, которую я собираюсь уронить к её ногам.

Учитель философии. Конечно, вы хотите написать ей стихи?

Г-н Журден. Нет, нет, только не стихи.

Учитель философии. Вы предпочитаете прозу?

Г-н Журден. Нет, я не хочу ни прозы, ни стихов.

Учитель философии. Так нельзя: или то, или другое.

Г-н Журден. Почему?

Учитель философии. По той причине, сударь, что мы можем излагать свои мысли не иначе, как прозой или стихами.

Г-н Журден. Не иначе, как прозой или стихами?

Учитель философии. Не иначе, сударь. Все, что не проза, то стихи, а что не стихи, то проза.

В известной сказке Л.Кэролла Белый Рыцарь намерен спеть Алисе «очень, очень красивую песню»:

— Когда я её пою, все рыдают… или…

— Или что? — спросила Алиса, не понимая, почему Рыцарь вдруг остановился.

В другой популярной сказке народный лекарь Богомол заключает после осмотра Буратино:

— Одно из двух: или пациент жив, или он умер. Если он жив — он останется жив или не останется жив. Если он мёртв — его можно оживать или нельзя оживить.

Это напоминает ситуацию из старой песенки, в которой тоже используется идея исключительного третьего:

Жила одна старушка,

И, если не скончалась —

Закон исключённого третьего кажется самоочевидным. Тем не менее высказывались предложения отказаться от него или ограничить его действие применительно к определённым высказываниям.

В частности, Аристотель сомневался в приложимости этого закона к высказываниям о будущих событиях. В настоящий момент наступление некоторых из них ещё не предопределено. Нет причины ни для того, чтобы они произошли, ни для того, чтобы они не случились. «Через сто лет в этот же день будет идти дождь» — это высказывание сейчас, скорее всего, ни истинно, ни ложно. Таким же является его отрицание. Но закон исключённого третьего утверждает, что или само высказывание, или его отрицание истинно. Значит, заключает Аристотель, хотя и без особой уверенности, данный закон следует ограничить одними высказываниями о прошлом и настоящем и не прилагать его к высказываниям о будущем.

Немецкий философ Гегель весьма иронично отзывался как о законе противоречия, так и о законе исключённого третьего. Последний он представлял, в частности, в такой форме: дух является зелёным или не является зелёным, и задавал каверзный, как ему казалось, вопрос: какое из этих двух утверждений истинно?

Ответ на этот вопрос не представляет, однако, труда. Ни одно из двух утверждений: «Дух — зелёный» и «Дух — не зелёный» не является истинным, поскольку оба они бессмысленные. Закон исключённого третьего приложим только к осмысленным высказываниям. Только они могут быть истинными или ложными. Бессмысленное же не истинно и не ложно.

Резкой, но хорошо обоснованной критике подверг закон исключённого третьего голландский математик Л. Брауэр. В начале этого века он опубликовал три статьи, в которых выразил сомнение в неограниченной приложимости законов логики и прежде всего — закона исключённого третьего. Первая статья не превышала трех страниц, вторая — четырех, а вместе они не занимали и семнадцати страниц. Но впечатление, произведённое ими, было чрезвычайно сильным.

Брауэр был убеждён, что логические законы не являются абсолютными истинами, не зависящими от того, к чему они прилагаются. Возражая против закона исключённого третьего, он настаивал на том, что кроме утверждения и его отрицания имеется ещё третья возможность, которую нельзя исключить. Она обнаруживает себя при рассуждениях о бесконечных множествах объектов.

Допустим, что утверждается существование объекта с определённым свойством. Если множество, в которое входит этот объект, конечно, то можно перебрать все объекты. Это позволит выяснить, какое из следующих двух утверждений истинно: «В данном множестве есть объект с указанным свойством» или же «В этом множестве нет такого объекта». Закон исключённого третьего здесь справедлив.

Но когда множество бесконечно, объекты его невозможно перебрать. Если в процессе перебора будет найден объект с требуемым свойством, первое из указанных утверждений подтвердится. Но если найти этот объект не удастся, ни о первом, ни о втором из утверждений нельзя ничего сказать, поскольку перебор не проведён до конца. Закон исключённого третьего здесь не действует: ни утверждение о существовании объекта с заданным свойством, ни отрицание этого утверждения не является истинным.

Ограничение Брауэром сферы действия этого закона существенно сужало круг тех способов рассуждения, которые применимы в математике. Это сразу же вызвало резкую оппозицию многих математиков, особенно старшего поколения. «Изъять из математики принцип исключённого третьего, — заявлял немецкий математик Д. Гильберт, — все равно, что запретить боксёру пользоваться кулаками.

Критика Брауэром закона исключённого третьего привела к созданию нового направления в логике — так называемой интуиционистской логики. В последней не принимается данный закон и отбрасываются все те способы рассуждения, которые с ним связаны. Среди них — доказательства путём приведения к противоречию, или абсурду.

С законом исключённого третьего косвенно связан следующий методологический принцип: анализ каждого объекта должен вестись до тех пор и быть настолько полным, чтобы относительно любого утверждения об этом объекте можно было решить, истинно оно или нет. Это требование полноты и всесторонности исследования не относится, конечно, к законам логики. Оно полезно, но нередко оказывается невыполнимым. В случае рассуждений о бесконечных и неопределённых совокупностях объектов, об изменяющихся, текущих состояниях и т.п. изучение объекта не всегда способно достичь такой полноты, чтобы на любой вопрос о нем удалось ответить однозначно «да» или «нет».

www.e-reading.club

Формула закона исключённого третьего: из двух противоречащих мыслей одна является истинной,

а вторая ложной; третьего не дано (закону исключённого третьего подчиняются только противоречащие мысли).

Закон исключённого третьего (лат. tertium non datur, то есть «третьего не дано») — закон классической логики, состоящий в том, что из двух высказываний — «А» или «не А» — одно обязательно является истинным, то есть два суждения, одно из которых является отрицанием другого, не могут быть одновременно ложными. Закон исключённого третьего является одним из основополагающих принципов «классической математики».

Нарушение закона исключенного третьего: можно либо лишиться («потерять, утратить что-либо», либо нет; нельзя представить косвенно и лишиться наполовину. Масштабы того кровопролития можно представить даже по косвенным данным, зная, что малые деревни… лишились половины здоровых мужчин.

Хоть небольшое, но хорошее подспорье для молодой семьи.

Здесь не соблюдается третий закон логики – закон исключенного третьего. Как мы помним, непременное условие соблюдения третьего закона логики – то, что сопоставляемые высказывания должны быть действительно противоречивыми, т. е. такими, между которыми нет и не может быть среднего, третьего, промежуточного понятия. Они должны исключать друг друга. Небольшое и хорошее никак не являются противоположными, это тот случай, который легко соотносится с юмористическим: «Пенсия у меня хорошая, но маленькая», ведь известно, что когда о пенсии говорят «хорошая», имеют в виду именно ее достаточный для жизни

10. Закон достаточного основания: сущность, практическое значение.

Формула закона достаточного основания: всякая правильная мысль доказана.

Желать добра в умственном труде – это значит понимать все сильные и слабые стороны ребенка…

Нарушение закона достаточного основания вызванный отсутствием причинно-следственных связей между содержанием первого и второго предложений. В первом предложении – подмена понятий. Желать добра ребенку, приучая его к умственному труду, значит – давать ему посильные задания, учитывая все его сильные и слабые стороны.

… много разных битв произошло на земле, и все они доказывают, что не обязательно войной, а в пределах разума можно договориться по любым вопросам.

Это нарушение закона достаточного основания. Противоположные понятия – война и мир, а не война и разум, кроме того, войны как раз показывают, что, не найдя мирного решения проблемы, государства вступают в войну. Это негуманно, но едва ли шведы добровольно отдали Петру Первому подходы к морю. Соответственно: …много разных битв произошло на земле, и все они доказывают, что война – не лучшее решение проблем, всегда следует стремиться к мирным переговорам по любым вопросам. В предложении есть и стилистическая ошибка – есть устойчивое выражение «в пределах разумного», вероятно, автор хотел использовать именно его. Выражения «в пределах разума» в русском языке нет, поскольку у разума (в русской ментальности) нет предела.

studfiles.net

ЗАКОН ИСКЛЮЧЁННОГО ТРЕТЬЕГО

Философия: Энциклопедический словарь. — М.: Гардарики . Под редакцией А.А. Ивина . 2004 .

Новая философская энциклопедия: В 4 тт. М.: Мысль . Под редакцией В. С. Стёпина . 2001 .

Смотреть что такое «ЗАКОН ИСКЛЮЧЁННОГО ТРЕТЬЕГО» в других словарях:

Закон исключённого третьего — (лат. tertium non datur, то есть «третьего не дано») закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, то есть два суждения, одно из которых является… … Википедия

Исключённого третьего закон — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

Исключённого третьего принцип — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

Принцип исключённого третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

Закон исключенного третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

Закон исключения третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

Закон Пирса — Закон Пирса один из законов классической логики, аналог законов двойного отрицания и исключённого третьего. Назван в честь американского логика и философа Чарльза Пирса. Закон Пирса формально выглядит так: что означает: P должно быть… … Википедия

Закон противоречия — Закон непротиворечия (закон противоречия) закон логики, который гласит, что два несовместимых (противоречащих либо противоположных) суждения не могут быть одновременно истинными. По крайней мере, одно из них необходимо ложно[1].… … Википедия

Закон двойного отрицания — положенный в основу классической логики принцип, согласно которому «если неверно, что неверно А, то А верно». Закон двойного отрицания называется также законом снятия двойного отрицания. В формализованном языке логики высказываний закон двойного… … Википедия

Принцип исключенного третьего — Закон исключённого третьего закон классической логики, состоящий в том, что из двух высказываний «А» или «не А» одно обязательно является истинным, т.е. два суждения, одно из которых является отрицанием другого, не могут быть одновременно… … Википедия

dic.academic.ru