Сила. Три закона Ньютона

Понятие силы в механике — это ключевое понятие. Ключевое — значит основное. Как чупа-чупс без палочки станет обычной никому не интересной карамелькой, так и механика (а точнее — динамика) без силы будет набором непонятной абракадабры.

Из жизни мы знаем, что тела могут действовать друг на друга: мальчик толкает тележку, Солнце притягивает Землю, магнит притягивает железные предметы и т.д.

Сила — это физическая величина, которая как раз таки и характеризует взаимодействие между телами. Сила показывает:

• в каком направлении одно тело действует на другое;
• насколько сильно одно тело действует на другое.

Итак, сила — это направление и величина. Где-то у нас такое уже было. Конечно, было: это же все вектора у нас имеют направление и величину (длину). А это значит, что сила — это вектор. Обозначается сила (если это не какая-то конкретная сила) буквой F ⃗ \vec F ⃗ .

Но на одно и то же тело может действовать несколько тел сразу. Например, тот же железный болт может одновременно притягиваться двумя магнитами:

Логика и наш жизненный опыт подсказывают нам, что притягивать будут оба магнита одновременно. И болт будет притягиваться некоторой «средней силой» так, как будто вместо этих двух магнитов действует один магнит, расположенный примерно посередине между двумя настоящими магнитами.

Все верно. Именно так и будет. А результирующая сила (мы для понятности назвали ее «средняя сила») — это сумма двух сил:

Напомним вам, что силы — это векторы. А векторы складываются двумя способами:

• по правилу треугольника
• по правилу параллелограмма.

В нашем примере мы сложили силы по правилу параллелограмма. Если вам непонятен способ сложения векторов, рекомендуем посмотреть тему » Два вида физических величин: скалярные величины и векторные величины «.

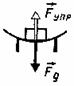
Правильное название «средней силы» — равнодействующая сила . Равнодействующую силу находят в том случае, если на тело действует сразу несколько сил. Фактически равнодействующая сила — это результат суммарного действия всех сил.

На тело, находящееся на горизонтальной плоскости, действуют две горизонтальные силы (см. рисунок, вид сверху).

Три закона Ньютона

Три закона Ньютона определяют «правила жизни» в механике. Обычно в школе их излагают в прямой последовательности — от первого закона к третьему. Мы поступим по-другому. Мы изложим их в обратном порядке. Нам кажется, что так будет понятнее. Приступим.

Третий закон Ньютона . Попробуйте надавить рукой на стол. При этом ладонью своей руки вы почувствуете поверхность стола. И вы также почувствуете некоторое сопротивление со стороны стола. Будто и сам стол давит на вас. При этом, если бы вы не давили на стол, а держали руку неподвижно, а поверхность стола приближалась бы к вашей руке и сама давила на вашу руку, то ощущения были бы точно такими же .



Можно предположить, что когда тело А воздействует на другое тело — тело B (например, вы действуете на стол), — то и тело B действует на тело А.

Рассмотрим другой пример. Девочка А и девочка B стоят на коньках на льду. Девочка А начинает толкать девочку B. Наш жизненный опыт подсказывает нам, что девочка B будет двигаться в ту сторону, куда ее толкает девочка А. Но! Жизненный опыт нам подсказывает, что и девочка А начнет двигаться так, будто ее толкнула девочка B.

Это подтверждает нашу догадку, что когда тело А действует с некоторой силой на тело B, то и тело B действует на тело А.

Оказывается, что наше предположение — верное. Более того, силы, с которыми тела действуют друг на друга, одинаковые (!).

Итак, третий закон Ньютона звучит следующим образом:

Силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению: F ⃗ 1 → 2 = − F ⃗ 2 → 1 . \vec_=-\vec_ <.>F ⃗ 1 → 2 ​ = − F ⃗ 2 → 1 ​ .

Второй закон Ньютона . Представьте себе ситуацию: на столе неподвижно стоит мячик. Мы толкаем его, то есть мы действуем силой . При этом мячик начинает двигаться. Значит, у него появилась скорость .

Итак, сначала мячик покоился и у него была нулевая скорость: V 1 = 0 V_1=0 V 1 ​ = 0 . А затем мячик двигался, и его скорость была уже не нулевой: V 2 ≠ 0 V_2\neq 0 V 2 ​ ≠ 0 . То есть скорость изменилась (!). У нас есть изменение скорости. А это значит, что есть ускорение.

Итак, можно сделать вывод, что сила придает телу ускорение, она «создает» ускорение тела. Логично будет предположить, что бОльшая сила даст мячику бОльшее ускорение: ускорение тела тем больше, чем больше сила. Но это еще не все.

Возьмем два мячика: легкий шарик для пинг-понга и тяжелый железный шарик из подшипника. Подействуем на них одинаковой силой. Оба они получат ускорение. Но ускорение будет разное. Это подсказывает нам жизненный опыт.

Более тяжелый (массивный, с большей массой ) стальной шарик получит небольшую скорость; его ускорение будет небольшим.

Легкий (с меньшей массой ) шарик для пинг-понга получит большую скорость; ускорение у него будет большим.

Как правильно записать связь ускорения, массы и силы?

Итак, мы готовы к тому, чтобы записать второй закон Ньютона. Он звучит так:

Куда в этот момент направлен вектор действующей на точку силы?

Первый закон Ньютона . Наконец-то мы дошли до первого закона Ньютона. Напомним, что

• третий закон Ньютона говорит нам о том, как тела взаимодействуют друг с другом ;
• второй закон Ньютона говорит о том, что происходит с самим телом при действии силы;
• а вот первый закон Ньютона.

А первый закон Ньютона говорит о том, где (при каких условиях) работают 3-й и 2-й законы Ньютона. Оказывается, 2-й и 3-й законы Ньютона работают только в инерциальных системах отсчета.

Инерциальные системы отсчета — это системы отсчета, в которых тела двигаются равномерно, прямолинейно и поступательно (или же находятся в состоянии покоя), если на тела не действуют никакие другие тела или действие этих тел скомпенсировано.

«Ух, как сложно», — можете сказать вы. «Да, вы правы», — ответим мы вам. Если говорить по-простому, то инерциальные системы — это системы, в которых тела, на которые не действуют силы (или их суммарное действие равно нулю), будут либо стоять на месте, либо двигаться с постоянной скоростью в неизменном направлении. В таких системах любое изменение скорости (то есть наличие ускорения) связано только с действием силы. Скорость не может меняться, если нет силы.

А вот в НЕинерциальных системах скорость тела может меняться без силы. То есть может меняться беспричинно.

Пример: представьте, что вы стоите в центре автобуса с полностью затонированными стеклами. И этот «пацанский» автобус равномерно едет по идеально ровной дороге. Находясь внутри, вы даже не чувствуете, что автобус едет.

В какой-то момент автобус резко тормозит. Что будет происходить с вами? Жизненный опыт подсказывает нам, что что вы резко «полетите» вперед. При этом на вас не действует никакая сила. То есть вы начинаете двигаться относительно автобуса без всякой причины. Автобус — это пример неинерциальной системы отсчета. Неинерциальные системы отсчета — это системы, которые двигаются с ускорением. В них не работают законы Ньютона. Тела в таких системах отсчета могут беспричинно менять свою скорость. С такими системами мы работать не будем.

Нашу Землю можно условно отнести к инерциальным системам отсчета. Почему? Земля на самом деле неинерциальна. Неинерциальна она потому, что Земля вращается. А это значит, что Земля двигается с центростремительным ускорением. А такие системы (двигающиеся с ускорением) являются неинерциальными. Но так как Земля вращается достаточно медленно, то и центростремительное ускорение получается небольшим. Поэтому условно Землю можно считать инерциальной системой отсчета.

lampa.io

Закон на нютон



1.7. Первый закон Ньютона. Масса. Сила

При движении тела его скорость 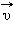может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением 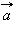. В кинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела. Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.

Взаимодействием тел принято называть взаимное влияние тел на движение каждого из них.

Раздел механики, изучающий законы взаимодействия тел, называется динамикой.

Законы динамики были открыты в 1687 г. великим ученым И. Ньютоном. Сформулированные им закона динамики лежат в основе так называемой классической механики. Законы Ньютона следует рассматривать как обобщение опытных фактов. Выводы классической механики справедливы только при движении тел с малыми скоростями, значительно меньшими скорости света c .

Самой простой механической системой является изолированное тело , на которое не действуют никакие тела. Так как движение и покой относительны, в различных системах отсчета движение изолированного тела будет разным. В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением.

Первый закон Ньютона (или закон инерции ) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем .

Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.

Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией . Поэтому первый закон Ньютона называют законом инерции .

Впервые закон инерции был сформулирован Г. Галилеем (1632 г.). Ньютон обобщил выводы Галилея и включил их в число основных законов движения.

В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.

При описании движения тел вблизи поверхности Земли системы отсчета, связанные с Землей, приближенно можно считать инерциальными. Однако, при повышении точности экспериментов, обнаруживаются отклонения от закона инерции, обусловленные вращением Земли вокруг своей оси.

Примером тонкого механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко . Так называется массивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей, была инерциальной, плоскость качаний маятника Фуко относительно Земли оставалась бы неизменной. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятника на поверхность Земли имеет вид розетки (рис. 1.7.1).



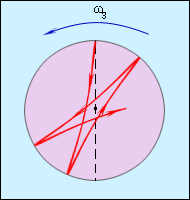
С высокой степенью точности инерциальной является гелиоцентрическая система отсчета (или система Коперника), начало которой помещено в центр Солнца, а оси направлены на далекие звезды. Эту систему использовал Ньютон при формулировании закона всемирного тяготения (1682 г.).

Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система, связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы (см. §1.2).

Итак, причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу .

Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.

Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т. е. в процессе взаимодействия оба тела приобретают ускорения. Отношение ускорений двух данных тел оказывается постоянным при любых воздействиях. В физике принято, что массы взаимодействующих тел обратно пропорциональны ускорениям, приобретаемым телами в результате их взаимодействия.



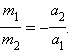
В этом соотношении величины 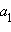и 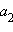следует рассматривать как проекции векторов 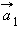и 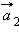на ось OX (рис. 1.7.2). Знак «минус» в правой части формулы означает, что ускорения взаимодействующих тел направлены в противоположные стороны.

В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг) .

Масса любого тела может быть определена на опыте путем сравнения с массой эталона ( m _эт = 1 кг ). Пусть m ₁ = m _эт = 1 кг . Тогда



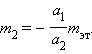
Масса тела – скалярная величина . Опыт показывает, что если два тела с массами m ₁ и m ₂ соединить в одно, то масса m составного тела оказывается равной сумме масс m ₁ и m ₂ этих тел:

physics.ru

Объединение учителей Санкт-Петербурга

Сила. Первый закон Ньютона

СИЛА.

Сила – векторная физическая величина, являющаяся мерой взаимодействия тел. Обозначение: .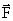

Существует 4 основных типа взаимодействия: гравитационное, электромагнитное, сильное, слабое.

Все взаимодействия являются проявлениями этих основных типов.

Примеры сил: сила тяжести, сила упругости, вес тела, сила трения, выталкивающая (архимедова) сила, подъемная сила.

Сила характеризуется:

1. Величиной (модулем);

2. Направлением;

3. Точкой приложения.

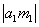Из опыта по взаимодействию следует: или . Величина характеризует действие второго тела на первое, а величина 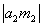— характеризует действие первого тела на второе. Т.к. взаимодействие одно и то же, то величину, равную произведению массы тела на ускорение, полученное в данном взаимодействии, можно принять за меру взаимодействия: 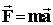. Внимание: вектора ускорения и силы всегда сонаправлены!



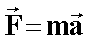
Т.к. сила – векторная величина, то силы складываются векторно (правила параллелограмма и треугольника). Складывать можно только силы, приложенные к одному телу. Сила, равная векторной сумме всех действующих на тело сил, называетсяравнодействующей: .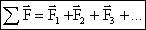



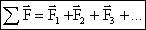
СИ: 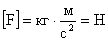Сила равна одному ньютону, если тело массой 1 кг приобретает ускорение 1м/с 2 .



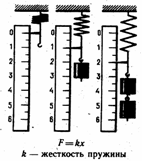
Измерение силы: силы измеряются динамометром по сравнению величины измеряемой силы с силой упругости пружины. Используется линейная зависимость между величиной силы упругости и удлинением пружины.

Для правильного измерения силы необходимо, чтобы при измерении

тела покоились или двигались прямолинейно и равномерно!

Динамометр градуируется известной силой тяжести.



1-й закон Ньютона.

Роль 1-го закона – он определяет, в каких СО выполняются законы динамики.

Существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно или покоится, если на него не действуют другие тела или их действия скомпенсированы.

Другая формулировка: существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно или покоится, если равнодействующая всех сил, действующих на тело, равна нулю.

Инерциальные системы отсчета.

СО, в которых выполняется 1-й закон Ньютона, называются инерциальными системами отсчета (ИСО).

Свойство ИСО: все СО, движущиеся прямолинейно и равномерно относительно данной ИСО, тоже являются инерциальными. СО, движущиеся относительно любой ИСО с ускорением, являются неинерциальными

В реальной жизни абсолютной ИСО не существует. СО можно считать инерциальной с той или иной степенью точности в определенных задачах. Например, Землю можно считать ИСО при исследовании движения автомобиля и нельзя – при исследовании полета ракеты (необходимо учитывать вращение).

Принцип относительности Галилея.

Все ИСО – равноправны: законы механики одинаковы во всех ИСО.

Опыт: чем больше сила, тем больше изменение скорости тела (ускорение) — .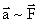

www.eduspb.com

Основные ссылки

Второй и третий законы Ньютона.

2-й закон Ньютона.

Ускорение, полученное телом в результате взаимодействия, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела: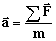. Выражение справедливо для любых сил любой природы.

Непосредственно решает основную задачу динамики.





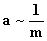
Сила (равнодействующая сил) определяет только ускорение тела. Величины скорости и перемещения могут быть любыми в зависимости от начальных условий.

Третий закон Ньютона.

Из опыта: 1. .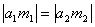

2. Ускорения взаимодействующих тел направлены по одной прямой в противоположных направлениях. Вывод: 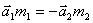или .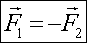

Любые два тела взаимодействуют силами одной природы направленными вдоль одной прямой, равными по величине и противоположными по направлению.







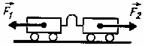
Свойства этих сил:

1. Всегда действуют парами.
2. Одной природы.
3. Приложены к разным телам! (F₁— к первому телу, F₂ – ко второму телу). Нельзя складывать! Не уравновешивают друг друга!

   

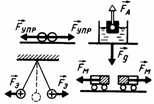
   Система законов динамики. Законы Ньютона выполняются в системе, т.е. одновременно и только в инерциальных системах отсчета. 1-й закон позволяет отобрать ИСО. 2-й закон позволяет по известным силам найти ускорение тела. 3-й закон позволяет связать между собой взаимодействующие тела. Все эти законы следуют из опыта.

   Законы механики Ньютона

   В отсутствие внешних силовых воздействий тело будет продолжать равномерно двигаться по прямой.

   Ускорение движущегося тела пропорционально сумме приложенных к нему сил и обратно пропорционально его массе.

   Всякому действию сопоставлено равное по силе и обратное по направлению противодействие.

   Законы Ньютона — в зависимости от того, под каким углом на них посмотреть, — представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки — блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.

   Однако Исаак Ньютон взял названные в его честь законы не из воздуха. Они, фактически, стали кульминацией долгого исторического процесса формулирования принципов классической механики. Мыслители и математики — упомянем лишь Галилея (см. Уравнения равноускоренного движения) — веками пытались вывести формулы для описания законов движения материальных тел — и постоянно спотыкались о то, что лично я сам для себя называю непроговоренными условностями, а именно — обе основополагающие идеи о том, на каких принципах зиждется материальный мир, которые настолько устойчиво вошли в сознание людей, что кажутся неоспоримыми. Например, древним философам даже в голову не приходило, что небесные тела могут двигаться по орбитам, отличающимся от круговых; в лучшем случае возникала идея, что планеты и звезды обращаются вокруг Земли по концентрическим (то есть вложенным друг в друга) сферическим орбитам. Почему? Да потому, что еще со времен античных мыслителей Древней Греции никому не приходило в голову, что планеты могут отклоняться от совершенства, воплощением которой и является строгая геометрическая окружность. Нужно было обладать гением Иоганна Кеплера, чтобы честно взглянуть на эту проблему под другим углом, проанализировать данные реальных наблюдений и вывести из них, что в действительности планеты обращаются вокруг Солнца по эллиптическим траекториям (см. Законы Кеплера).

   Первый закон Ньютона

   Учитывая столь серьезный, исторически сложившийся провал, первый закон Ньютона сформулирован безоговорочно революционным образом. Он утверждает, что если какую-либо материальную частицу или тело попросту не трогать, оно будет продолжать прямолинейно двигаться с неизменной скоростью само по себе. Если тело равномерно двигалось по прямой, оно так и будет двигаться по прямой с неизменной скоростью. Если тело покоилось, оно так и будет покоиться, пока к нему не приложат внешних сил. Чтобы просто сдвинуть физическое тело с места, к нему нужно обязательно приложить стороннюю силу. Возьмем самолет: он ни за что не стронется с места, пока не будут запущены двигатели. Казалось бы, наблюдение самоочевидное, однако, стоит нам отвлечься от прямолинейного движения, как оно перестает казаться таковым. При инерционном движении тела по замкнутой циклической траектории его анализ с позиции первого закона Ньютона только и позволяет точно определить его характеристики.

   Представьте себе что-то типа легкоатлетического молота — ядро на конце струны, раскручиваемое вами вокруг вашей головы. Ядро в этом случае движется не по прямой, а по окружности — значит, согласно первому закону Ньютона, его что-то удерживает; это «что-то» — и есть центростремительная сила, которую вы прилагаете к ядру, раскручивая его. Реально вы и сами можете ее ощутить — рукоять легкоатлетического молота ощутимо давит вам на ладони. Если же вы разожмете руку и выпустите молот, он — в отсутствие внешних сил — незамедлительно отправится в путь по прямой. Точнее будет сказать, что так молот поведет себя в идеальных условиях (например, в открытом космосе), поскольку под воздействием силы гравитационного притяжения Земли он будет лететь строго по прямой лишь в тот момент, когда вы его отпустили, а в дальнейшем траектория полета будет всё больше отклоняться в направлении земной поверхности. Если же вы попробуете действительно выпустить молот, выяснится, что отпущенный с круговой орбиты молот отправится в путь строго по прямой, являющейся касательной (перпендикулярной к радиусу окружности, по которой его раскручивали) с линейной скоростью, равной скорости его обращения по «орбите».

   Теперь заменим ядро легкоатлетического молота планетой, молотобойца — Солнцем, а струну — силой гравитационного притяжения: вот вам и ньютоновская модель Солнечной системы.

   Такой анализ происходящего при обращении одного тела вокруг другого по круговой орбите на первый взгляд кажется чем-то само собой разумеющимся, но не стоит забывать, что он вобрал в себя целый ряд умозаключений лучших представителей научной мысли предшествующего поколения (достаточно вспомнить Галилео Галилея). Проблема тут в том, что при движении по стационарной круговой орбите небесное (и любое иное) тело выглядит весьма безмятежно и представляется пребывающим в состоянии устойчивого динамического и кинематического равновесия. Однако, если разобраться, сохраняется только модуль (абсолютная величина) линейной скорости такого тела, в то время как ее направление постоянно меняется под воздействием силы гравитационного притяжения. Это и значит, что небесное тело движется равноускоренно. Кстати, сам Ньютон называл ускорение «изменением движения».

   Первый закон Ньютона играет и еще одну важную роль с точки зрения нашего естествоиспытательского отношения к природе материального мира. Он подсказывает нам, что любое изменение в характере движения тела свидетельствует о присутствии внешних сил, воздействующих на него. Условно говоря, если мы наблюдаем, как железные опилки, например, подпрыгивают и налипают на магнит, или, доставая из сушилки стиральной машины белье, выясняем, что вещи слиплись и присохли одна к другой, мы можем чувствовать себя спокойно и уверенно: эти эффекты стали следствием действия природных сил (в приведенных примерах это силы магнитного и электростатического притяжения соответственно).

   Второй закон Ньютона

   Если первый закон Ньютона помогает нам определить, находится ли тело под воздействием внешних сил, то второй закон описывает, что происходит с физическим телом под их воздействием. Чем больше сумма приложенных к телу внешних сил, гласит этот закон, тем большее ускорение приобретает тело. Это раз. Одновременно, чем массивнее тело, к которому приложена равная сумма внешних сил, тем меньшее ускорение оно приобретает. Это два. Интуитивно эти два факта представляются самоочевидными, а в математическом виде они записываются так:

   где F — сила, m — масса, а — ускорение. Это, наверное, самое полезное и самое широко используемое в прикладных целях из всех физических уравнений. Достаточно знать величину и направление всех сил, действующих в механической системе, и массу материальных тел, из которых она состоит, и можно с исчерпывающей точностью рассчитать ее поведение во времени.

   Именно второй закон Ньютона придает всей классической механике ее особую прелесть — начинает казаться, будто весь физический мир устроен, как наиточнейший хронометр, и ничто в нем не ускользнет от взгляда пытливого наблюдателя. Назовите мне пространственные координаты и скорости всех материальных точек во Вселенной, словно говорит нам Ньютон, укажите мне направление и интенсивность всех действующих в ней сил, и я предскажу вам любое ее будущее состояние. И такой взгляд на природу вещей во Вселенной бытовал вплоть до появления квантовой механики.

   Третий закон Ньютона

   За этот закон, скорее всего, Ньютон и снискал себе почет и уважение со стороны не только естествоиспытателей, но и ученых-гуманитариев и попросту широких масс. Его любят цитировать (по делу и без дела), проводя самые широкие параллели с тем, что мы вынуждены наблюдать в нашей обыденной жизни, и притягивают чуть ли не за уши для обоснования самых спорных положений в ходе дискуссий по любым вопросам, начиная с межличностных и заканчивая международными отношениями и глобальной политикой. Ньютон, однако, вкладывал в свой названный впоследствии третьим закон совершенно конкретный физический смысл и едва ли замышлял его в ином качестве, нежели как точное средство описания природы силовых взаимодействий. Закон этот гласит, что если тело А воздействует с некоей силой на тело В, то тело В также воздействует на тело А с равной по величине и противоположной по направлению силой. Иными словами, стоя на полу, вы воздействуете на пол с силой, пропорциональной массе вашего тела. Согласно третьему закону Ньютона пол в это же время воздействует на вас с абсолютно такой же по величине силой, но направленной не вниз, а строго вверх. Этот закон экспериментально проверить нетрудно: вы постоянно чувствуете, как земля давит на ваши подошвы.

   Тут важно понимать и помнить, что речь у Ньютона идет о двух силах совершенно разной природы, причем каждая сила воздействует на «свой» объект. Когда яблоко падает с дерева, это Земля воздействует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно устремляется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с равной силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, это уже следствие второго закона Ньютона. Масса яблока по сравнению с массой Земли низка до несопоставимости, поэтому именно его ускорение заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно. (В случае падения яблока центр Земли смещается вверх на расстояние менее радиуса атомного ядра.)

   По совокупности же три закона Ньютона дали физикам инструменты, необходимые для начала комплексного наблюдения всех явлений, происходящих в нашей Вселенной. И, невзирая на все колоссальные подвижки в науке, произошедшие со времен Ньютона, чтобы спроектировать новый автомобиль или отправить космический корабль на Юпитер, вы воспользуетесь все теми же тремя законами Ньютона.

   elementy.ru