Правило ломаная линия
1. В суффиксах страдательных причастий прошедшего времени пишется нн ; как правило, эти причастия имеют приставки или пояснительные слова: исправле нн ая рукопись; правле нн ые корректором гранки.
При отсутствии приставок или пояснительных слов пишется одно н; ср.: замощё нн ые дороги — мощё нн ые булыжником дороги — мощё н ые дороги. В этом случае перед нами прилагательное, образованное от страдательного причастия прошедшего времени: правле н ый текст, беше н ый волк, вяле н ая вобла, глаже н ые брюки, дра н ая куртка, золочё н ые изделия, лома н ая линия, пута н ый ответ, рва н ая рана, сея н ые травы, стира н ое бельё ит. п.
2. Разграничение страдательных причастий и образованных от них прилагательных (тем самым выбор написания нн или н ) иногда производится не по формальному признаку, а по смысловому значению. Например- в предложении Будучи раненным, солдат оставался в строю в слове раненным пишется нн, несмотря на отсутствие приставки и пояснительных слов: оно сохраняет глагольное значение, указывает не на постоянный признак-качество, а на временное состояние, т. е. является причастием. Отглагольное прилагательное не обозначает действия и отвечает на вопрос: «какой?» («какая?», «какое?», «какие?»).
В приставочных образованиях, даже если они имеют значение прилагательного, пишется нн: выдержа нн ое вино, наложе нн ым платежом, подержа нн ые книги, поноше нн ое платье, ускоре нн ый шаг. Но: назва́ н ый брат, посажё н ый отец, смышлё н ый мальчик.
Запомните: во второй части сложных образований глаженые-переглаже н ые брюки, латаная-перелата н ая шуба, ношеный-переноше н ый костюм, стираное-перестира н ое бельё, штопаные-перештопа н ые чулки и т. п. , несмотря на наличие приставки пере-, целесообразно писать одно н, так как сложное слово в целом имеет значение прилагательного (высокая степень качества).
Примечание. При переходе причастия в прилагательное возможно изменение лексического значения слова: верченый парень (‘ветреный, легкомысленный’); конченый человек (‘ни на что больше уже не способный’); писаная красавица (‘красивая, как на картине’); Прощёное воскресенье (‘последнее воскресенье перед Великим постом’).
3. Наличие приставки не- на написание отглагольного прилагательного не влияет: неезже н ый, нехоже н ый, незва н ый, непроше н ый, некоше н ый, некраше н ый, некрещё н ый, неписа н ый (закон), непуга н ый.
4. В составе сложного слова написание отглагольного прилагательного также не меняется: гладкокрашеный, горячекатаный, холоднокатаный, цельнокатаный, цельнокроеный, домотканый, пестротканый, златотканый, златокованый, малоезженый, малохоженый, малоношеный, малосолёный, мелкодроблёный, свежегашёный, свежемороженый и др. (ср. с терминами, в которых вторая часть сложного слова образована от приставочного глагола: гладкоокрашенный, малонаезженный, свежезамороженный и др.).
5. Два н ( нн ) пишется в бесприставочных причастиях, образованных от глаголов совершенного вида: броше нн ый, да нн ый, купле нн ый, лишё нн ый, пленё нн ый и др., а также в немногих причастиях, образованных от глаголов несовершенного вида: вида нн ый, виде нн ый, слыха нн ый, чита нн ый и др.
6. Отглагольные прилагательные на -ованн(ый), -ёванн(ый) пишутся с нн : балова нн ый ребёнок, корчёва нн ый участок.
Примечания: 1. В прилагательных кованый и жёваный сочетания -ое- и -ев- входят в состав корня.
2. В существительных, образованных от страдательных причастий и отглагольных прилагательных, пишется нн или н в соответствии с производящей основой:
варе н ик, копче н ости, мороже н ое, муче н ик, труже н ик, уче н ик
бесприда нн ица, воспита нн ик, да нн ик, избра нн ик, свяще нн ик, ставле нн ик, утопле нн ик
То же самое относится к производным наречиям: дела нн о улыбаться; нежда нн о-негада нн о явиться; пута н о отвечать.
7. В кратких формах страдательных причастий пишется одно н. В кратких отглагольных прилагательных (как и в отыменных) сохраняется написание нн. Отглагольные прилагательные отвечают на вопрос «каков?» («какова?», «каково?», «каковы?»). Ср.:
Мировая общественность была взволнована сообщениями о гибели космонавтов.
Игра актёра была проникновенна и взволнованна.
В период дворцовых переворотов в России многие фавориты были приближены ко двору и возвышены.
Идеалы и стремления первых революционеров были возвышенны.
Иногда простые вопросы бывают искусственно запутаны.
Сюжеты этих произведений сложны и запутанны .
Вам всегда везёт, вы, по-видимому, избалованы судьбой.
При неправильном воспитании дети обычно капризны и избалованны.
С точки зрения логики эти выводы мало или даже совсем не обоснованы.
Масштабы работ были ограничены отпущенными средствами.
Его возможности ограниченны (т. е. малы).
Врачи были озабочены состоянием больного.
Шторм усиливался, и лица моряков были серьёзны и озабоченны.
Предъявленные нам требования произвольны и необоснованны.
Суд не усмотрел в данном деле состава преступления, и обвиняемые были оправданы.
Чрезвычайные меры в этих условиях были необходимы и вполне оправданны.
Все варианты дальнейшей игры шахматистом до конца продуманы.
Ответы экзаменующихся были содержательны и продуманны.
Примечание. Некоторые отглагольные прилагательные пишутся в полной форме с двумя н ( нн ), а в краткой — с одним н , подобно причастиям, с которыми их сближает наличие приставки и вид производящего глагола: заплака нн ые глаза — глаза заплака н ы; заржавле нн ые ножи — ножи заржавле н ы; поноше нн ое платье — платье поноше н о.
То же в сложных словах: общепризна нн ое превосходство — превосходство общепризна н о; свежезамороже нн ые ягоды — ягоды свежезамороже н ы.
8. Некоторые прилагательные допускают двоякое написание краткой формы в зависимости от значения и конструкции. Ср.:
Сестра намерена вскоре уехать (‘имеет намерение’ — в сочетании с инфинитивом).
Его дерзость намеренна (‘нарочита’ — без инфинитива).
Мы преданы Родине (в сочетании с формой дательного падежа).
Старые друзья всегда преданны (без дополнения).
Наши легкоатлеты уверены в победе (с дополнением).
Движения гимнастов легки и уверенны (без дополнения)
old-rozental.ru


Ло́маная (ломаная линия) — геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами.
Определение
Ломаной (ломаной линией)  называется фигура, которая состоит из отрезков
называется фигура, которая состоит из отрезков  ,
,  , .
, .  . Точки
. Точки  ,
,  , .
, .  называются вершинами ломаной, а отрезки
называются вершинами ломаной, а отрезки  ,
,  , .
, .  — звеньями ломаной.
— звеньями ломаной.
В случае если  ломаная называется замкнутой. В этом случае дополнительно требуют чтобы отрезки
ломаная называется замкнутой. В этом случае дополнительно требуют чтобы отрезки  и
и  не лежали на одной прямой.
не лежали на одной прямой.
Типы ломаных
Ломаная может иметь самопересечения:
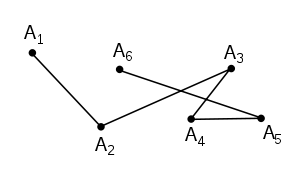
Если первая и последняя точки ломаной совпадают, то такая ломаная называется замкнутой.
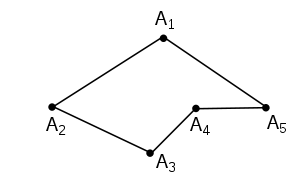
Изображённую здесь ломаную следует называть A1A2A3A4A5A1. Замкнутую ломаную можно также называть многоугольником. В этом случае изображённая фигура будет называться «многоугольник» A1A2A3A4A5«
Wikimedia Foundation . 2010 .
Смотреть что такое «Ломаная» в других словарях:
ломаная — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ЛОМАНАЯ — последовательность отрезков (звеньев), конец каждого из которых (кроме последнего) является началом следующего и смежные отрезки не лежат на одной прямой … Большая политехническая энциклопедия
ломаная — ▲ линия ↑ состоящий из, прямая (линия), отрезок который, располагаться, под углом ломаная линия, у которой смеж … Идеографический словарь русского языка
Ломаная — ж. Линия, состоящая из отрезков прямой линии, соединяющихся под углом. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Ломаная пирамида — Ломаная пирамида … Википедия
Ломаная линия — Ломаная A1A2A3A4A5A6 Ломаной (ломаной линией) A1A2. An называется фигура, которая состоит из отрезков A1A2, A2A3, . An 1An. Точки A1, A2, . An называются вершинами ломаной, а отрезки A1A2, A2A3, . An 1An − звеньями ломаной. При этом… … Википедия
Ломаная аллея — Санкт Петербург Общая информация Район города Петроградский Исторический район Острова Прежние названия Западная Ломаная аллея Протяжённость 240 м Ближайшие станции метро … Википедия
Ломаная улица (Санкт-Петербург) — Ломаная улица Санкт Петербург Общая информация Район города Московский Полицейская часть Нарвская часть Прежние названия Ломанская улица, Ломанная улица Протяжённость 470 м Ближайшие станции метро … Википедия
ломаная зрительная труба геодезического прибора — ломаная труба Зрительная труба геодезического прибора, у которой оптическая ось ломаная линия. [ГОСТ 21830 76] Тематики приборы геодезические Обобщающие термины основные узлы и принадлежности геодезических приборов Синонимы ломаная труба EN… … Справочник технического переводчика
Ломаная улица — Улица проходит от Московских ворот до Цветочной улицы. Название присвоено 5 марта 1871 года и связано с тем, что, как написано в этом указе, «улица имеет несколько заворотов». То же самое про нее можно сказать и сейчас. В 1912 году улицу… … Санкт-Петербург (энциклопедия)
dic.academic.ru
Урок математики в 1-м классе. Тема: «Ломаная линия»
Продолжительность урока: 35 минут
Тип урока: Изучение и первичное закрепление нового материала.
Цель: Познакомить с ломаной линией и ее компонентами.
Задачи урока:
1) Образовательная:
- познакомить учащихся с ломаной линией и её видами; усвоение понятий «ломаная», «звено ломаной линии», «вершина ломаной»;
- повторить: отрезки, линии;
- совершенствование вычислительных умений и навыков.
- развивать логическое мышление, пространственное воображение, внимание, память, фантазию;
- совершенствовать уровень развития математической речи
- показать межпредметную связь математики и астрономии.
- воспитывать коммуникативные качества учащихся
- воспитывать гордость за свою отчизну, достижения в науке, технике, космонавтике.
2) Развивающие:
3) Воспитывающие:
Материалы и оборудование:
- Мультимедийная презентация
- Компьютер, проектор, экран
- «Учебный маршрутный лист»
- Карандаши: жёлтый, синий, красный
- Спагетти, кусочек пластилина
- Массажные коврики для стоп, СУ-ДЖОК (массажный набор «Каштан» для кистей рук)
Ведущий вид деятельности: продуктивный, творческий, проблемный
Методы работы: объяснительно-иллюстративные, частично-поисковые, словесные, наглядные, практические.
Функция учителя: организатор сотрудничества; консультант, управляющий поисковой работой.
Педагогические технологии:
— педагогика сотрудничества (учебный диалог);
Ожидаемый результат:
- знать что такое ломаная линия, из чего она состоит, чем отличается от отрезка, луча, прямой линии, кривой линии
- расширение знаний о геометрическом материале
- повышение активности учащихся на уроках
- использование учащимися приобретённых знаний и умений в практической деятельности
- обогащение словарного запаса
- Как называются фигуры? (точка, треугольник, кривая линия, прямая линия, отрезок)
- А чем луч отличается от отрезка?
- А чем прямая отличается от луча?
Список использованной литературы.
1. Истомина Н.Б. Математика: учебник для 1 класса общеобразовательных учреждений. — Смоленск: «Ассоциация XXI век», 2008.
2. Истомина Н.Б. Рабочая тетрадь к учебнику «Математика» для 1 класса
3. Методические рекомендации к учебнику «Математика» 1 класс, под ред. Н.Б.Истоминой.- Смоленск: «Ассоциация ХХI век». 2006 год.
Ход урока
1. Оргмомент
Слайд 1. Звучит голос И.Левитана с сообщением о первом полёте человека в космос.
Учитель: Дети, 2011 год объявлен в нашей стране годом Российской космонавтики. А кто из вас интересуется космосом? Кто хочет полететь в космос? Сегодня представляется такая возможность для всего класса. Мы совершим учебный полёт. Чтобы не совершать ошибок во время полёта, нужно подготовиться, восстановить некоторые знания. Как вы думаете, что нам необходимо вспомнить?
Дети: Повторить числа, сложение и вычитание.
Учитель: Я соглашусь с вами, дети. Добавлю: нужно знать пройденные геометрические фигуры.
2. Актуализация прежних знаний
Учитель: На ваших столах лежат «Учебные маршрутные листы». Все результаты работы на уроке будем заносить на эти листы.
Познакомьтесь с новым словом. «Астроно?мия» (др.- греч.) образован от древнегреческих слов «астрон» — звезда и «номос» — закон или культура, и дословно означает «Закон звёзд».
Все учёные — астрономы знают математику на «отлично». Без этих знаний невозможны точные подсчёты расстояний до далёких звёзд, при строительстве космических кораблей, их траектории движения, развития скорости:
Итак, первое задание: «математический диктант». Прослушайте условие, высчитайте в уме, запишите только ответ.
Из 9 планет солнечной системы только две имеют женские имена. А сколько мужских имён в названиях планет солнечной системы? (7)
У созвездии «Большая медведица» 7 ярких звёзд. А в созвездии «Кассиопея» 5 ярких звёзд. На сколько больше ярких звёзд в созвездии Большая медведица? (2)
На мой вопрос в начале урока: «Кто мечтает полететь в космос?» ответили «да» 3 девочки и 7 мальчиков. Сколько всего ребят нашего класса хотят слетать в космос? (10)
Дети: записывают ответы в свои «Учебные маршрутные листы», а одному ученику — «командиру отряда космонавтов» поручается написать ответы на доске. Затем все дети проверяют, сопоставляют свои результаты с ответами, записанными на доске.
Слайд №2
Почему вторая фигура называется треугольником? (имеет три вершины и три стороны)
— Можно ли стороны треугольника назвать отрезками? Почему? (стороны треугольника — отрезки, т.к. линии их образующие имеют границы)
Учитель: В «Учебном маршрутном листе» найдите красную точку и постройте луч. Какой инструмент необходим? (Линейка)
Соедините две синие точки. Какая фигура у вас получилась? (Отрезок)
Через жёлтую точку проведите прямую линию. Можете провести ещё одну? А ещё? (Да!)
Верно, через одну единственную точку можно провести бесчисленное количество прямых линий.
3. Физкультминутка (Ребята выполняют упражнения, стоя у парт)
Раз, два!
Скорость света!
Три, четыре!
Мы летим!
На далёкие планеты
Поскорей попасть хотим!
Чтоб водить корабли,
Чтобы в небо взлететь,
Надо многое знать.
Надо много уметь!
И при этом, и при этом
Вы заметьте-ка,
Очень важная наука
Ма-те-ма-ти-ка!4. Введение нового материала
Сегодня мы продолжаем путешествие в страну Геометрию.
Посмотрите, что у меня в руках? (Вермишель спагетти)
Какую геометрическую фигуру она вам напоминает? (Прямую линию)
Возьмите в руки спагетти, которые раздал вам дежурный. Переломите в середине, а затем каждую часть ещё раз переломите пополам.
Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)
Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)
Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)
Я должна немного поправить вас, она называется «ломаная» линия.
Посмотрите, из чего состоит ломаная линия? (Из отрезков)
Каждая ломаная линия состоит из нескольких отрезков — звеньев. Сколько звеньев в этой ломаной? (Четыре)
Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, называется вершиной.
Сколько вершин у данной ломаной линии? (Три)
Кроме того, у ломаной линии есть 2 конца.
5. Физкультминутка — самомассаж пальцев кистей рук с помощью массажёра СУ-ДЖОК: Слайд №4
По — порядку
Все планеты
Назовёт любой из нас:
Раз — Меркурий,
Два — Венера,
Три — Земля,
Четыре — Марс,
Пять — Юпитер,
Шесть — Сатурн.
Семь — Уран,
Восьмой — Нептун.
А за ним уже потом,
Под названием Плутон.6. Первичное закрепление
Учитель: Дети, давайте вспомним ещё раз, какими бывают кривые линии? (Замкнутыми и незамкнутыми)
А как вы думаете, ломаные линии могут быть замкнутыми и незамкнутыми?
Учитель открывает на доске таблицу № 1:
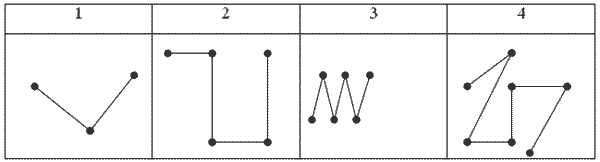
— Какие фигуры изображены в таблице? (ломаные линии)
— У какой ломаной больше всего звеньев? (№ 4)
— У какой ломаной меньше всего звеньев? (№ 1)
— Какая ломаная имеет три вершины? (№ 2)
— Какая ломаная имеет пять вершин? (№ 4)
Учитель открывает на доске таблицу №2:
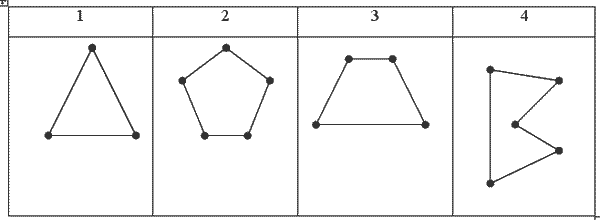
Учитель: Это тоже ломаные линии. Чем они отличаются от ломаных линий на первой таблице? (Все звенья соединены между собой)
— Такие ломаные линии называют «замкнутыми», а линии на первой таблице — «незамкнутыми» линиями.
— Назовите замкнутую ломаную линию, которая имеет меньше всего звеньев. (№1)
Верно, а может ли быть замкнутая линия из двух звеньев, подумайте. Давайте построим такую ломаную линию. (Нет, чтобы «замкнуть» линию нужно третье звено)
Учитель: Найдите и назовите на карте звёздного неба созвездия: незамкнутые ломаные линии и замкнутые.
Учитель: Если вашу «ломаную линию из спагетти» лежащую на парте, перевернуть, то будет напоминать созвездие «Кассиопею». Она была названа в честь царицы, которую заколдовала коварная колдунья.
7. Физкультминутка.
Для глаз. Дети следят за движением Колобка на Слайде№4
Задание на внимание
На несколько секунд я покажу вам одну фигуру. Вы должны запомнить её и выложить из счётных палочек точно такую.
Теперь поработайте в парах. Проверьте внимание своего одноклассника.
Какая фигура у вас получилась?
Что вы ещё скажете о ней? Можно ли её назвать ломаной линией?
Можно ли назвать её замкнутой? (незамкнутой?) Почему?
8. Подведение итога урока
С какой геометрической фигурой познакомились? (Ломаной линией)
Из каких элементов состоит ломаная линия? (Из звеньев и вершин)
Какие бывают ломаные линии? (Замкнутые и незамкнутые)
Переверните «Учебный маршрутный лист». Обведите цветным карандашом только ломаные линии, замкнутые и незамкнутые:
Какую линию описал корабль Ю.Гагарина за 108 минут вокруг Земли? (незамкнутую кривую линию)
В правом нижнем уголке «Учебного маршрутного листа» вам «улыбается» звёздочка. Какую геометрическую фигуру она напоминает? (Замкнутую ломаную линию) Определите количество вершин? Звеньев? Есть ли концы?
Самооценка работы учащихся на уроке:
У вас 3 цветных карандаша. Закрасьте звёздочку в зелёный цвет, если полностью довольны своей работой на уроке; жёлтым — доволен, но не полностью; красным — надо постараться!
Дополнительный материал (Слайды 18 — 31): сведения о планетах, звёздах, освоении космоса.
xn--i1abbnckbmcl9fb.xn--p1ai
Определение и характеристики ломаной геометрической фигуры
 Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.
Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.
Это интересно: разность чисел – что это, как ее найти?
Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.
Звенья, вершины и длина
Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:
-
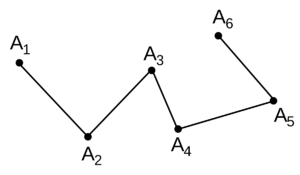 Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено. - Точки соединения концов этих отрезков называются вершинами.
- Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
- Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
- Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:
- Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
- Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).
В целом такую совокупность принято называть ABCDE или EDCBA.
Обратите внимание: что такое луч в геометрии.
Разновидности
В геометрии принято различать несколько разновидностей по структуре:
- Замкнутые самопересекающиеся.
- Незамкнутые самопересекающиеся.
- Замкнутые без самопересечений.
- Незамкнутые без самопересечений.
Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.
Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.
Многоугольники
Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.
 Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.
Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.
Ниже приведены основные свойства, общие для всех многоугольников:
- Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
- Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
- Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
- Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
- Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
- Если все стороны и углы многоугольника равны, он называется правильным.
Треугольники
Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.
Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.
Различают следующие виды треугольников:
- Равносторонние — все стороны их равны по длине.
- Разносторонние — все стороны различаются по длине.
- Равнобедренные — две стороны из трех имеют одинаковую длину.
- Остроугольные — если все углы острые.
- Прямоугольные — если имеется прямой угол.
- Тупоугольные — если есть один тупой угол.
Четырехугольники
Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.
Если все углы у четырехугольника прямые — это прямоугольник.
Правильный четырехугольник носит название квадрата.
Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.
obrazovanie.guru
Математика
Строка навигации
Прямая и ломаная линии
Прямая линия
Прямая линия есть кратчайшее расстояние между двумя точками.
Свойства прямой. a) Положение прямой линии вполне определяется теми двумя точками, между которыми она проведена.
Это свойство зависит от того, что b) между двумя точками можно провести только одну прямую линию, ибо между двумя точками существует только одно кратчайшее расстояние.
Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.
В прямой линии нужно отличить ее положение и ее длину.
Прямую линию можно неопределенно продолжать в обе стороны.
Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.
c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.
d) Через одну точку можно провести бесчисленное множество прямых линий.
Все линии на чертеже 5 проходят через общую точку A.
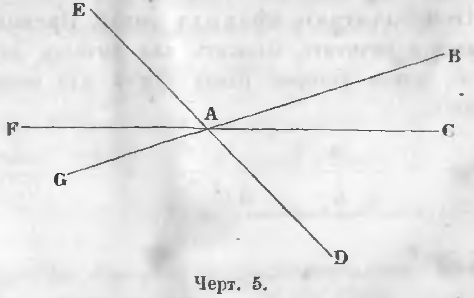
e) Если две прямые имеют две общие точки, то они совпадают всеми остальными точками.
f) Расстояние между двумя точками определяется длиной прямой линии, их соединяющей.
Равные прямые. Две прямые линии, имеющие одинаковую длину, называются равными. Линии AB с CD (черт. 6) будут равными линиями.

Равные прямые совпадают при наложении друг на друга.
Сравнение прямых линий
Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A.
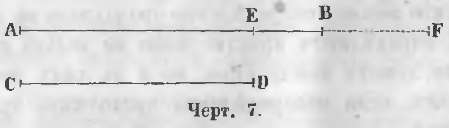
Здесь могут быть три случая:
Если точка D упадет в точку E, находящуюся между A и B, линия CD меньше AB.
Если точка D упадет в точку B, линия CD равна AB.
Если точка D упадет в точку F, находящуюся на продолжении линии AB, линия CD больше AB.
Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.
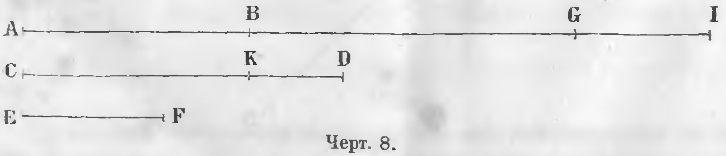
Чтобы сложить прямые линии AB, CD, EF (черт. 8), продолжают линию AB и от точки B откладывают линию BG, равную CD, от точки G линию GI равную EF. Линия AI равна сумме всех этих трех линий.
Чтобы найти разность линий CD и AB, откладывают на линии CD от точки C линию CK, равную AB, тогда линия KD равна разности линий CD и AB.
Отношение двух прямых линий
Сравнивая две прямые линии по длине, определяют их взаимное отношение. При этом сравнении имеет значение линия, называемая общей мерой двух линий.
Общая мера двух линий есть такая линия, которая содержится целое число раз в обеих линиях.
При определении взаимного отношения двух прямых линий по длине, могут встретиться два случая:
Когда эти линии имеют общую меру.
Когда они ее не имеют.
В первом случае они называются соизмеримыми, во втором — несоизмеримыми. В первом случае отношение двух линий выражается каким-нибудь рациональным, т. е. целым или дробным числом; во втором оно не может быть точно выражено ни целым, ни дробным числом.
Если две прямые линии соизмеримы, то находят их общую меру.
Определение общей меры двух линий
Общая мера двух линий большей AB и меньшей CD (черт. 9) не может быть больше линии CD. Удостоверимся сначала, не будет ли меньшая линия CD этой общей мерой.
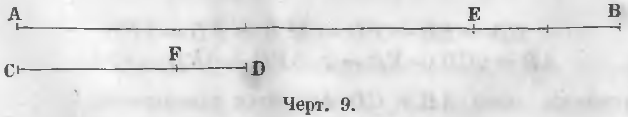
Для этого накладывают меньшую линию на большую и определяют, сколько раз она уложится в большей. Если она укладывается ровное число раз, например, m раз, тогда отношение двух линий выражается этим целым числом m.
AB = m * CD и AB/CD = m.
Если же она не укладывается ровное число раз, то последовательно накладывают линию CD до тех пор, пока не получится остатка EB меньшего CD.
Положим, линия CD уложилась в AB два раза и получился еще остаток EB. Общая мера линий AB и CD не может быть более остатка EB.
Действительно, из равенства
видно, что общая мера линий AB и CD должна содержаться равное число раз в линии EB. Она может или равняться линии EB или быть меньше ее.
Общая мера двух линий AB и CD должна быть общей мерой меньшей линии и остатка EB.
Отыскивая общую меру CD и EB, поступаем по предыдущему. Откладываем линию EB на линии CD до тех пор, пока не получится остатка FD, меньшего линии EB. Общая мера CD и EB будет по предыдущему заключению общей мерой EB и FD.
Линию FD снова откладываем по линии EB. Пусть линия FD отложится на линии EB ровно два раза, тогда линия FB и будет этой общей мерой.
Связь между линиями выразится рядом равенств:
AB = 2CD + EB
CD = EB + FD
EB = 2FDCD = EB + FD = 2FD + FD = 3FD
AB = 2CD + EB = 2 * 3FD + 3FD = 8FD.Отношение линий AB и CD выразится равенством:
AB/CD = 8FD/3FD = 8/3.
Мы видим, что при нахождении общей меры нужно поступать точно так же, как при нахождении общего наибольшего делителя между целыми числами. Отсюда
Правило нахождения общей меры двух линий. Чтобы найти общую меру, нужно меньшую линию наложить на большую, первый остаток на меньшую, второй остаток на первый, и поступить так до тех пор, пока последний остаток не уложится ровное число раз в предпоследнем.
Чтобы найти отношение двух линий, нужно при помощи общей меры выразить обе линии и потом найти частное этих выражений.
2-й случай: две прямые линии несоизмеримы. Если две линии несоизмеримы, мы никогда не получим такого остатка, который содержался бы в предпоследнем остатке целое число раз. В этом случае определяют отношение прямых линий с каким угодно приближением. Для этого разделив меньшую линию на n равных частей, накладывают это часть CE на большую линию AB (черт. 10). Положим, что эта часть повторяется в большей линии m раз и еще получается остаток FB меньше CE.

AB = mCE + FB
CD = nCE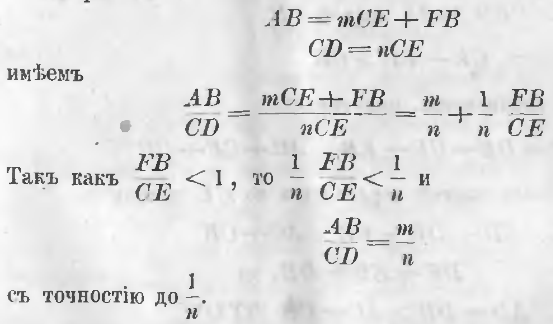
Так как n можно увеличивать произвольно, то и отношение длин двух прямых можно выразить с каким угодно приближением.
(См. о несоизмеримости диагонали квадрата с его стороной).
Измерение линий. Измерить линию значит найти ее отношение к другой линии, принятой за единицу. Это отношение называют длиной данной линии. Длина линии всегда выражается в каких-нибудь единицах.
Ломаные линии
Две линии ACB и ADB (черт. 11), соединяющие концы прямой AB, называются ломаными. При этом линия ACB называется внутренней, а линия ADB внешней ломаной линией.
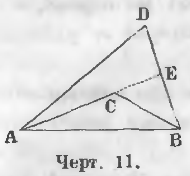
Теорема 1. Внешняя ломаная больше внутренней.
Даны две ломаные линии: внешняя ADB и внутренняя ACB (черт. 11).
Требуется доказать, что ADB больше ACB или
Доказательство. Продолжим линию AC до пересечения с линией DB в точке E.
Линия ADE как ломаная больше прямой AE.
Ломаная линия CEB больше прямой CB
Сложив эти неравенства, получим:
AD + DE + CE + EB > AC + CE + CB
Вычтя из обоих частей неравенства по CE, получим:
AD + DE + EB > AC + CB
Так как DE + EB = DB, то
Что и требовалось доказать.
Теорема 2. Сумма пересекающихся частей ломаных больше суммы непересекающихся.
Даны пересекающиеся ломаные ABC и ADC (черт. 12), AD и BC их пересекающиеся части.
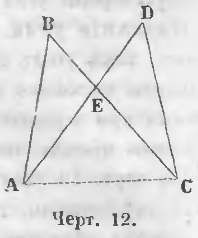
Требуется доказать, что
Доказательство. Из того, что ломаная AEB больше прямой AB и ломаная CED больше прямой DC вытекают неравенства:
maths-public.ru
