Закони додавання
· Комутативний (переставний) закон: «Для будь-яких цілих невід’ємних чисел а і b виконується рівність: а + b = b + а.»
Доведення. Нехай а – кількість елементів множини A,b – кількість елементів множини B, тобто n(A) = а, n(B) = b і А 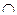 В =
В = 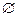 . Тоді за означенням суми цілих невід’ємних чисел а + b = n (A
. Тоді за означенням суми цілих невід’ємних чисел а + b = n (A 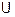 B). А так як A
B). А так як A 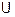 B = B
B = B 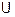 A (за комутативним законом об’єднання множин), то n (A
A (за комутативним законом об’єднання множин), то n (A 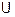 B) = n (B
B) = n (B 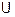 A)
A) 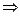 за означенням суми n (B
за означенням суми n (B 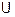 A) = b + а
A) = b + а 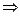 а+b = b+а для будь-яких цілих невід’ємних чисел.
а+b = b+а для будь-яких цілих невід’ємних чисел.
· Асоціативний (сполучний) закон: «Для будь-яких цілих невід’ємних чисел а , b, с виконується рівність: (a + b) + с = а + (b + с)».
Доведення. Нехай а – кількість елементів множини A, b – кількість елементів множини B, с – кількість елементів множини С, тобто n (A) = а, n (B) = в, n (С) = с, А 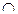 В =
В = 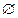 , B
, B 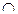 С =
С = 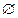 . Тоді за означенням суми двох цілих невід’ємних чисел (а + b) + с = n (A
. Тоді за означенням суми двох цілих невід’ємних чисел (а + b) + с = n (A  B) + n (C) = n ((A
B) + n (C) = n ((A  B)
B)  C). Так як за асоціативним законом об’єднання множин (A
C). Так як за асоціативним законом об’єднання множин (A  B)
B)  С = =A
С = =A  (B
(B  C), то n ((A
C), то n ((A  B)
B)  С) = n (A
С) = n (A  (B
(B  C))
C)) 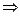 за означенням суми двох чисел n (A
за означенням суми двох чисел n (A  (B
(B  C)) = n (A) + n (B
C)) = n (A) + n (B  C) = а + (b + с)
C) = а + (b + с) 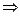 (а + b) + + с = а + (b + с).
(а + b) + + с = а + (b + с).
· Властивість монотонності додавання: «Для будь-яких цілих невід’ємних чисел а , b, m таких, що а = b виконується рівність: 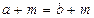 ».
».
Наслідкиіз комутативного та асоціативного законів додавання:
· Додавання числа до суми і суми до числа.
Додати число до суми або суму до числа можна двома способами: обчислити суму і до результату додати дане число або додати це число до одного з доданків, а до результату додати другий доданок.
· Додавання суми до суми.
Для того щоб додати суму до суми, можна до одного з доданків першої суми додати один із доданків другої, а до другого доданку першої суми – інший доданок другої суми і одержані результати додати.
Ці правила легко поширити на будь-яку кількість доданків і об’єднати їх одним правилом: якщо при додаванні маємо дужки, то їх можна опустити і об’єднати між собою доданки в будь-якій послідовності так, щоб обчислення виконувати найзручнішим способом.
Із законами дії додавання учні початкових класів знайомляться поступово: спочатку вивчають переставну властивість додавання (1 клас), яка використовується при складанні таблиць додавання одноцифрових чисел, а далі для розкриття прийомів додавання та раціоналізації обчислень. В 4 класі при узагальненні і систематизації знань про дію додавання закони – переставний і сполучний формулюються та записуються у буквеному вигляді.
Тема. Віднімання цілих невід’ємних чисел
1. Теоретико-множинний смисл різниці двох цілих невід’ємних чисел.
2. Означення різниці через суму. Зв’язок дії віднімання з дією додавання.
3. Умови існування різниці, її єдиність.
4. Правила віднімання.
5. Відношення «більше на», «менше на».
6. Прості задачі, які розв’язуються дією віднімання.
studopedia.com.ua
Сполучний закон суми










301. Прочитай пояснення про дію додавання та її закони. Будь-які два натуральних числа можна додати. Числа, які додають, називають доданками, а результат додавання — сумою. Наприклад: 7 + 5 = 12. Тут 7 і 5 — доданки, а 12 — сума. Знак додавання + (плюс). Дію додавання можна визначити за допомогою послідовності натуральних чисел.
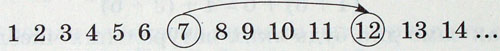
Позначимо в цьому ряді число 7. Відлічимо від нього вправо п’ять чисел. Дістанемо число 12, яке називається сумою чисел 7 і 5.
Переставний закон додавання. Позначимо в натуральному ряді спочатку число 5, а потім відлічимо від нього сім чисел.
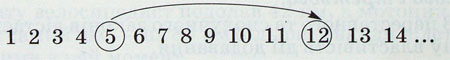
Дістанемо знову число 12. Отже,
Так само для будь-яких натуральних чисел a i b виконується рівність
яка виражає переставний закон додавання.
Від перестановки доданків сума не змінюється.
Сполучний закон додавання. Додамо три числа 4, 3 і 6. Спочатку до суми чисе 4 і 3, яка дорівнює 7, додамо число 6. Для цього від суми чисел 4 і 3, тобто від числа 7, відлічимо вправо 6 чисел. Дістанемо число 13.
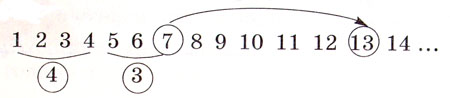
В обох випадках дістали одну й ту саму суму.
(4 + 3) + 6 = 4 + (3 + 6)
Так само для будь-яких натуральних чисел a, b i c виконується рівність
(a + b) + c = a + (b + c),
що виражає сполучний закон додавання.
Якщо до суми двох чисел потрібно додати третє число, можна до першого додати суму другого і третього.
З переставного та сполучного законів дістаємо ще одну властивість дії додавання.
У сумі кількох доданків можна переставляти доданки і брати їх у дужки будь-яким чином.
1+ 2 + 3 = 3 + 2 + 1
1 + 2 + 3 + 4 = (1 + 4) + (2 + 3)
34 + 249 + 26 = (34 + 26) + 249 = 60 + 249 = 309
edufuture.biz
Сполучний закон додавання (асоціативний);
Переставний закон додавання (комутативний).
Для будь-яких цілих невід’ємних чисел а і в виконується рівність а+в=в+а.
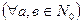
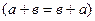
Доведення. Нехай 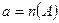 ,
,  і
і 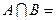 ○. Тоді за означенням суми цілих невід’ємних чисел:
○. Тоді за означенням суми цілих невід’ємних чисел: 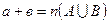 , але
, але  .
.
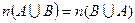 отже
отже 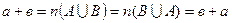 .
. 
Для будь-яких цілих невід’ємних чисел а, в, с виконується рівність (а+в)+с=а+(в+с).
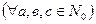
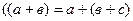
Доведення. Нехай 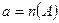 ,
,  ,
, 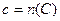 і
і 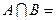 ○.
○.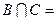 ○ Тоді за означенням суми двох чисел можна записати
○ Тоді за означенням суми двох чисел можна записати 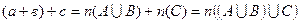 . Але так як об’єднання множин володіє сполучною властивістю
. Але так як об’єднання множин володіє сполучною властивістю 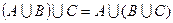 , то
, то 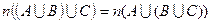 . Тоді
. Тоді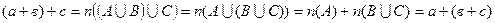 .
. 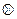
Сполучна властивість дозволяє знаходити суму трьох доданків. Для цього достатньо додати перший доданок до другого і до одержанного числа додати третій доданок, або додати перший доданок до суми другого і третього.
Переставний і сполучний закони можуть бути узагальнені на будь-яке число долданків. При цьому переставна властивість буде означати, що сума не зміниться при будь-якій перестановці доданків, а сполучний – що сума не зміниться при будь-якій групіровці доданків (без зміни порядку).
- Обчисліть, застосовуючи закони додавання
На основі переставної властивості переставимо доданки 36 і 281.
(на основі сполучного закону згрупуємо доданки, а потім знайдемо суми у дужках)
=(219+281)+(36+164)+52=500+200+52 = (застосуємо ще раз сполучний закон) =
З переставною властивістю учні знайомляться при вивченні додавання і віднімання в межах 10. Спочатку цей закон використовується при вивченні таблиць додавання. Наприклад, 5+6=6+5=11, 5+7=7+5=12. А потім вже для раціональних обчислень.
З сполучним законом учні знайомляться в 4-му класі і використовують придбані знання для раціональних обчислень.
(4 + 5) + 6 = переставимо місцями доданки 4 і 5 застосувавши переставну властивість додавання = (5+4)+6 = застосуємо сполучний закон = 5 + (4 + 6)
(30 + 7) + (10 + 4) = 30 + 7 + 10 + 4 = 30 + 10 + 7 + 4 = (30 + 10) + (7 + 4) = 40 + 11 = 51
273 + 1227 + 154 + 446 = (123 + 1227) + (154 + 446) = 1500 + 600 = 2100
ІV. Визначення відношення «менше» через додавання.
З’ясуємо на якій теоретичній основі проходить порівняння чисел.
Нехай дано два цілі невід’ємні числа а і в. З теоретико-множинної точки зору вони представляють число елементів скінчених множин А і В: а=n(А), в=n(В). Якщо ці множини рівнопотужні, то їм відповідає одне і те ж число, тобто а=в.
Числа а і в рівні, якщо вони визначаються рівно потужними множинами:
studopedia.su
Дія додавання
Закони додавання
4 клас
Тема уроку: Урок № 17. Дія додавання. Закони додавання
Вступ
Обчисліть приклади.
38 + 17 + 22 = 34 + 19 + 26 =
45 + 24 + 16 = 28 + 21 + 39 =
53 + 29 + 17 = 34 + 27 + 16 =
38 + 17 + 22 = 77 34 + 19 + 26 = 79
45 + 24 + 16 = 85 28 + 21 + 39 = 88
53 + 29 + 17 = 99 34 + 27 + 16 = 77
Пояснення нового матеріалу
Пригадайте, як називаються числа, які додають.
При додаванні числа називають доданками.
Як називають результат додавання?
Результат додавання називають сумою.
Дії додавання натуральних чисел властиві два закони. Перший називають переставним.
Переставний закон додавання: сума не змінюється від зміни місць доданків.
a + b = b + a
Переставний закон додавання можна визначити за допомогою натурального ряду чисел. Позначимо в натуральному ряді число 6. Відлічимо від нього вправо 8 чисел, отримаємо число 14.
6 + 8 = 14
А тепер зробимо навпаки: позначимо в натуральному ряді число 8. Потім управо від нього відлічимо 6 чисел. Знову вийде число 14.
8 + 6 = 14

Для трьох і більше доданків переставний закон додавання можна сформулювати так: числа можна додавати в будь-якому порядку.
Сполучний закон додавання: сума не змінюється, якщо доданки, що стоять поруч, замінити їх сумою.
(3 + 5) + 7 = 3 + (5 + 7)
Перевіримо сполучний закон додавання на натуральному ряді чисел.
Спочатку до суми чисел 3 і 5, яка дорівнює 8, додамо число 7. Для цього від числа 8 відлічимо вправо 7 чисел. Отримаємо число 15.
Тепер до числа 3 додамо суму чисел 5 і 7. 5 + 7 = 12. Отже, треба від числа 3 відлічити вправо 12 чисел. У нас знову вийшло число 15. В обох випадках ми отримали одну й ту ж суму. Отож, до суми чисел 3 і 5 додати 7, дорівнює три додати до суми чисел 5 і 7.
(3 + 5) + 7 = 3 + (5 + 7)
Так само для будь-яких натуральних чисел виконується рівність: до суми чисел a і b додати c, дорівнює a додати до суми чисел b і c.
(a + b) + c = a + (b + c)
45 + 24 + 16 =
45 + 24 + 16 = 45 + (24 + 16)
Для чотирьох і більше доданків сполучний закон додавання сформульований так: при додаванні кількох чисел можна об’єднувати будь-які з них.
У сумі кількох доданків можна переставляти доданки і брати їх у дужки будь-яким чином
53 + 29 + 17 = 29 + 53 + 17 = 29 + (53 + 17) = 29 + 70 = 99
Первинне закріплення
Обчисліть приклади.
34 + 19 + 26 =
28 + 21 + 39 =
34 + 16 + 27 =
34 + 19 + 26 = 14 + 26 + 19 = 79
У прикладі для зручності обчислень переставимо місцями другий і третій доданки – 19 і 26. Тепер легко порахувати: 34 + 26 = 60, 60 + 19 = 79.
60
28 + 21 + 39 = 28 + (21 + 39) = 28 + 60 = 88
У прикладі скористаємося сполучним законом. Тобто, замінимо сумою другий і третій доданки. 21 + 39 = 60, 28 + 60 = 88.
50
34 + 27 + 16 = 27 + 34 + 16 = 27 + (34 + 16) = 27 + 50 = 77
У прикладі можна скористатися двома законами: і переставним, і сполучним. Спочатку переставимо місцями доданки 34 і 27. Потім – об’єднаємо 34 і 16. Так ми швидко полічимо: 34 + 16 = 50, а 27 + 50 = 77.
Підсумок уроку
Сьогодні на уроці ми вивчили переставний і сполучний закони додавання. Тепер ми зможемо швидко обчислювати приклади, в яких потрібно додати декілька доданків.
urok-ua.com
Додавання і віднімання багатоцифрових чисел
Основне завдання теми — узагальнити та систематизувати знання учнів про дії додавання і віднімання, розвинути навички усних обчислень з круглими числами, виробити міцні навички письмових обчислень, навчити використовувати взаємозв’язок дій додавання і віднімання для перевірки правильності обчислень.
Послідовність опрацювання матеріалу така: дія додавання, закони додавання та їх застосування, задачі на додавання; дія віднімання, задачі на віднімання; письмове додавання і віднімання багатоцифрових чисел; перевірка додавання відніманням; обчислення різниці, коли зменшуване містить кілька нулів; додавання кількох доданків; знаходження значень виразів на сумісні дії першого ступеня; обчислення значень виразів з дужками; додавання і віднімання іменованих чисел, виражених у мірах довжини, маси і часу; круглі числа та застосування способу округлення при додаванні та відніманні.
В кінці теми учнів ознайомлюють з поняттям швидкості, розв’язують задачі на знаходження відстані, часу, швидкості.
Розгляньмо зміст і методику опрацювання окремих тем.
Тема «Дія додавання. Закони додавання та їх застосування. Задачі на додавання».
Розповідь. Розпочинаємо вивчати нову тему: додавання і віднімання багатоцифрових чисел. Відомо, що додати можна будь-яких два натуральних числа. Числа, які додають, називають доданками, а результат додавання — сумою. Наприклад: 8 + 4=12. Тут числа 8 і 4 — доданки, а число 12 — сума. Знак додавання «+» (плюс).
Дію додавання можна означити за допомогою натуральної послідовності чисел (мал. 112). 
Мал. 112 204 Розділ IX. Нумерація багатоцифрових чисел і арифметичні дії в межах мільйона
Додати два натуральних числа, наприклад 8 і 4, означає знайти в натуральній послідовності таке число, що посідає четверте місце після 8.
Для дії додавання натуральних чисел характерні переставний і сполучний закони.
Переставний закон. Сума не змінюється від зміни місць доданків.
25 + 80 = 80 + 25 а + Ь=Ь + а
Для трьох і більше доданків переставний закон можна сформулювати так: числа можна додавати в будь-якому порядку.
Сполучний закон. Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього чисел. (7 + 8)»+ 32 = 7 + (8 + 32) (а+ Ь) + с = а + (Ь + с)
З переставного та сполучного законів дії додавання отримуємо таку її властивість: у сумі кількох доданків можна переставляти доданки і брати їх у дужки будь-яким чином.
З + 26 + 47 + 4 + 40 = (26 + 4 + 40) + (47 + 3).
Учитель пропонує учням проаналізувати кілька простих задач на дії першого ступеня і визначити, які з них розв’язуються дією додавання. Підсумовуючи їх відповіді, учитель повідомляє, що дією додавання розв’язують різні задачі: на знаходження суми чисел, на збільшення числа на кілька одиниць, на знаходження невідомого зменшуваного.
Тема «Дія віднімання. Віднімання суми від числа. Задачі на віднімання».
Розповідь. Відомо, що з рівності на додавання можна скласти рівність на віднімання.
8 + 3= 11, 11 -3 = 8.
Відніманням називається дія, за допомогою якої за даною сумою двох доданків і одним з них знаходять інший доданок.
Число, від якого віднімають, називається зменшуваним; число, яке віднімають, — від’ємником, а результат — різницею. Наприклад: 12-5 = 7. Тут 12 — зменшуване, 5 — від’ємник, а 7 — різниця.
За допомогою натуральної послідовності чисел дію віднімання можна сформулювати по-іншому.
Відняти натуральне число, наприклад 5, від 12 означає знайти в натуральній послідовності таке число, від якого 12 стоїть на п’ятому місці.
Для пояснення прийомів віднімання важливе значення має правило віднімання суми від числа.
Щоб від числа відняти суму двох інших чисел, достатньо послідовно відняти кожний доданок окремо.
З цього випливає, що число можна віднімати частинами. 43 — 9 = 43 — (3 + 6) = (43 — 3) — 6 = 40 — 6 = 34.
За допомогою дії віднімання розв’язують різні задачі: на знаходження
остачі, на зменшення числа на кілька одиниць, на різницеве порівняння, на знаходження невідомого доданка та від’ємника.
Тема «Письмове додавання і віднімання багатоцифрових чисел».
Учні вже ознайомлені з письмовим додаванням і відніманням трицифрових чисел, тому ознайомлення з діями в межах мільйона відбувається прямим перенесенням. Пропонується перевірити правильність обчислення двох виразів:
Учні повторно обчислюють вирази, пояснюють, як треба записувати числа при письмовому додаванні або відніманні.
Після цього вчитель повідомляє, що письмове додавання і віднімання багатоцифрових чисел виконують так само, як додавання і віднімання трицифрових чисел. Далі учні виконують фронтально чи самостійно різні вправи на застосування дій першого ступеня: обчислення числових виразів з буквеними компонентами; розв’язування рівнянь та різних простих і складених задач.
Перевірка віднімання додаванням. Учитель записує на дошці дві рівності: а — Ь = с; Ь + с = а.
Учні повинні на числових рівностях обгрунтувати, чому друга рівність буде правильною. Потім учитель повідомляє: якщо додати різницю і від’ємник, то отримаємо зменшуване. Цей зв’язок використовують для перевірки правильності виконання дії віднімання. Міркуємо так: якщо при додаванні різниці і від’ємника не отримаємо зменшуваного, то в обчисленнях допущено помилку.
Аналогічно на наступному уроці розглядають перевірку додавання відніманням. Тут використовують зв’язок: якщо а + Ь = с, то с — а = Ь.
Запис перевірки учні виконують поряд із записом на віднімання. Слово «перевірка» записувати не треба.
У процесі розв’язування прикладів з коментуванням пояс- з 005 нюють: обчислення різниці, коли у зменшуваному є кілька ну- і 126 лів; додавання кількох доданків; знаходження значень виразів і
879 на сумісні дії першого ступеня та виразів з дужками. Наведемо один зі зразків такого коментування.
Треба від числа 3 005 відняти 1 126. Від 5 од. відняти 6 од. не можна. Оскільки у розрядах десятків і сотень 0 од., то візьмемо 1 тис. Щоб не забути про це, у розряді тисяч поставимо крапку. Одна тисяча — це 10 сотень. 9 сот. залишимо у розряді сотень, а одну сотню перетворимо на десятки. Одна сотня — це 10 десятків. 9 дес. залишимо в розряді десятків, а один десяток перетворимо на одиниці. 1 дес. — це 10 од. Та ще 5 од., буде 15 од. 206 Розділ IX. Нумерація багатоцифрових чисел і арифметичні дії в межах мільйона
Від 15 од. відняти 6 од., буде 9 од. Пишемо 9 на місці одиниць. Від 9 дес. відняти 2 дес, буде 7 дес. Пишемо 7 на місці десятків. Від 9 сот. відняти 1 сот., буде 8 сот. Пишемо 8 на місці сотень. Від 2 тис. відняти 1 тис, буді 1 тис. На місці тисяч пишемо І. Різниця дорівнює 1 879.
Додавання і віднімання складених іменованих чисел виконують, перетворивші їх на прості іменовані числа. Після цього дії над ними виконують так само як і над натуральними числами. Проте учням слід вказати на можливісті виконання дій відразу над складеними іменованими числами. Поясненій, дають за зразками запису розв’язання.
46 м 05 см — 8 м 57 см = 37 м 48 см
_4 605 _46 м 05 см
З 748 (см) 37 м 48 см
§32. Множення і ділення багатоцифрових чисел
Основне завдання теми полягає у формуванні навичок письмового множення і ділення багатоцифрових чисел. Учні повинні вміти пояснювати виконувані дії. Треба систематизувати знання учнів про дії множення і ділення та їхні властивості.
Алгоритми дій множення і ділення різні. Тому прийоми виконання дій вводять почергово: після вивчення одного випадку множення вивчають аналогічний випадок ділення. Опрацювання матеріалу має таку послідовність: множення і ділення на одноцифрове число; множення і ділення на дво-і трицифрові розрядні числа; множення і ділення на двоцифрове число. У процесі вивчення теми розглядають ще такі питання: вимірювання площі, дроби, міри часу.
Множення на одноцифрове число. Відповідно до програми розглядають такі питання: поняття дії множення, переставний і сполучний закони дії імноження, розподільний закон множення відносно додавання, загальний випадок множення і особливі випадки множення, множення одноцифрового числа на багатоцифрове, множення іменованих чисел.
Тема «Дія множення. Закони множення. Задачі, які розв’язують дією множення».
Бесіда. Множення — особливий вид додавання: додавання однакових доданків. Помножити натуральне число 3 на натуральне число 5 означає знайти суму п’яти доданків, кожний з яких дорівнює 3.
3-5 = 3 + 3 + 3 + 3 + 3.
Числа 3 і 5 називаються множниками, а вираз 3 • 5 — їх добутком. Дії множення властиві переставний, сполучний та розподільний закони. Отож розгляньмо їх.
Переставний закон. Для будь-яких натуральних чисел а і Ь виконується рівність: а • Ь = Ь • а, що виражає переставний закон множення: від переставляння множників добуток не змінюється.
Методика викладання математики в початкових класах
Сполучний закон. Для будь-яких натуральних чисел а, Ь і с ппконується рівність: (а ■ Ь) • с = а • (Ь • с), що виражає сполучний закон множення: щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього чисел.
Наприклад: (3 • 5) • 2 = 3 • (5 • 2).
З переставного та сполучного законів дії множення отримуємо таку її шіастивість: у добутку кількох множників можна переставляти множники і брати їх у дужки будь-яким чином.
Наприклад: 3 • 4 • 25 • ЗО = (3 • ЗО) • (4 • 25).
Розподільний закон. Для будь-яких натуральних чисел а, Ь і с ііиконується рівність: (а + Ь) ■ с =а • с + Ь ■ с, що виражає розподільний іакон: добуток суми двох чисел на будь-яке число дорівнює сумі добутків кожного доданка на це число.
Розподільний закон виконується для будь-якого числа доданків. І Іаприклад: (1+2 + 3 + 4+5)-6=1-6 + 2-6 + 3-6 + 4-6 + 5-6.
За допомогою дії множення розв’язують задачі: на розкриття змісту дії множення; на збільшення числа в кілька разів; на кратне порівняння чисел; на знаходження невідомого діленого.
Тема «Множення багатоцифрових чисел на одноцифрове число (загальний ііипадок)».
У процесі підготовки до засвоєння письмового алгоритму множення повторюють табличні випадки множення, множення чисел 0 і 1, множення суми на число.
Опрацювання нового матеріалу. У 3 класі ми розглядали випадки письмового множення в межах 1000. Будемо вчитися множити письмово числа и межах мільйона.
Помножимо чотирицифрове число 2 317 на 4 спочатку усно. Розкладемо це число на розрядні доданки і будемо множити за правилом множення суми на число.
(2 000 + 300 + 10 + 7) • 4 = 8 000 + 1 + 200 + 40 + 28 = 9 268.
Усно знайти добуток можна, але без запису проміжних результатів зробити це важкувато. Треба в пам’яті одразу тримати багато чисел. Великі числа краще множити письмово, у стовпчик. Послухайте докладне пояснення.
Треба помножити 2 317 на 4. Записуємо другий множник _ _ _
під одиницями першого. Підводимо риску. Зліва ставимо знак х . множення «х». Розпочинаємо письмове множення з одиниць.
Множимо 7 од. на 4, буде 28 од. Це 2 дес. і 8 од.; 8 од. пишемо під одиницями, а 2 дес. запам’ятовуємо.
1 дес. помножити на 4, буде 4 дес. та ще 2 дес, буде 6 дес. Пишемо їх під десятками.
З сот. множимо на 4, буде 12 сот. Це 1 тис. і 2 сот.; 2 сот. пишемо під сотнями, а 1 тис. запам’ятовуємо.
2 тис. помножити на 4, буде 8 тис. та ще 1 тис, буде 9 тис. Пишемо їх на місці тисяч. Добуток 9 268. 208 Розділ ЇХ. Нумерація багатоцифрових чисел і арифметичні дії в межах мільйона
На цьому ж записі подаємо зразок короткого пояснення: треба помножити 2 317 на 4. 7 на 4, буде 28. 8 пишемо, а 2 запам’ятовуємо. 1 на 4, буде 4 та ще 2, буде 6. З на 4, буде 12, 2 пишемо, а 1 запам’ятовуємо. 2 на 4, буде 8 та ще 1, буде 9. Добуток 9 268.
При короткому поясненні опускаємо назви розрядних одиниць і міркування про перетворення проміжних результатів.
У процесі коментованого обчислення виразів учні користуються коротким поясненням, але в разі ускладнення або допущення помилки вчитель пропонує дати докладне пояснення. Зокрема, це стосується випадку множення, коли багатоцифрове число містить всередині кілька нулів (наприклад, 23 007 • 5).
Розглядаючи множення багатоцифрового числа, що закінчується одним або кількома нулями, вчитель звертає увагу учнів на те, що другий множник можна записати так, щоб нулі залишились праворуч.
Це можна пояснити так: множимо спочатку сотні, а Х36 900 потім сотні записуємо в одиницях (дописати 2 нулі).
У випадку множення одноцифрового числа на багатоцифрове застосовуємо переставну властивість дії множення.
Множення складених іменованих чисел на одноцифрове число виконують двома способами: відразу множать або спочатку замінюють складене іменоване число простим, виконують дію над абстрактними числами і потім просте іменоване число замінюють складеним.
13 грн. 64 коп. • 5 = 68 грн. 20 коп. 1 364
Ділення багатоцифрового числа на одноцифрове число. Перед вивченням ділення багатоцифрового числа на одноцифрове узагальнюють поняття про дію ділення та ЇЇ властивості.
Тема «Дія ділення. Властивості частки. Задачі, які розв’язують дією ділення».
Бесіда. Діленням називається дія, за допомогою якої за добутком двох множників і одним із цих множників знаходять інший множник. 80 • 3 = 240 240 : 3 = 80
Число 240 називається діленим, 3 — дільником, 80 — часткою. У множині натуральних чисел дія ділення не завжди виконується. Наприклад, щоб поділити 50 на 6, треба знайти таке число х, для якого: 6 • х — 50. Такого натурального числа не існує, бо 6 • 8 = 48, а 6 • 9 = 54.
У множині натуральних чисел завжди можливе ділення з остачею:
Розглянемо властивості, характерні для частки:
1. Щоб поділити число на добуток двох чисел, достатньо поділити цс число на один з множників, а потім результат поділити на інший множник, 120: (2-3) = 120:2:3 = 60: = 20.
2. Щоб поділити суму чисел на дане число, достатньо поділити кожний доданок на це число і додати здобуті частки. —
(48 + 36) : 6 = 48 : 6 + 36 : 6 = 8 + 6 = 14.
3. Щоб поділити різницю чисел на дане число, достатньо поділити на це число зменшуване і від’ємник, а потім від першої частки відняти другу.
(90 — 21): 3 = 90 : 3 — 21 : 3 = 30 — 7 = 23.
За допомогою дії ділення розв’язують задачі: на розкриття змісту дії ділення; на зменшення числа у кілька разів; на кратне порівняння чисел; на знаходження невідомого множника та дільника.
При підготовці до вивчення ділення багатоцифрового числа на одноцифрове необхідно виконати низку вправ, пов’язаних з безпосереднім визначенням при діленні кількості цифр у частці: 1. Який найвищий розряд у даному числі? 2. Скільки цифр буде в запису числа, якщо найвищий його розряд, наприклад, десятки тисяч? 3. Скільки всього десятків (сотень і т. д.) в даному числі? 4. Яке число визначає цифра, записана у вищому розряді даного числа (наприклад, 527)? 5. Яке число визначають дві перші цифри вищих розрядів даного числа?
Потрібно також нагадати учням зв’язок дії ділення з дією множення, повторити властивість ділення суми на число, випадки ділення з остачею.
Тема «Ділення багатоцифрового числа на одноцифрове (загальний випадок)».
Процес оволодіння діленням багатоцифрового числа на одноцифрове — один з найважчих у вивченні початкового курсу математики. Тут необхідні неодноразове докладне пояснення вчителя і тривале коментування самих учнів. Подамо зразок докладного пояснення.
Ділене 2 148, дільник 4. Виділимо перше неповне ділене. 21481 4 Вищий розряд діленого — тисячі. 2 тис. не можна поділити на 20 рЗУ
4 так, щоб у результаті отримати тисячі. Замінимо 2 тис. —гг ‘ сотнями і додамо 1 сот., отримаємо 21 сот. Отже, перше
неповне ділене 21 сот., тому вищим розрядом частки будуть —-
сотні, і, таким чином, у частці буде три цифри. Позначимо 28
місця цих цифр крапками. 23
Визначимо першу цифру частки. 21 сот. поділимо на 4, буде 0
5 сот. Визначимо, скільки всього сотень поділили. Для цього помножимо 5 сот. на 4, отримаємо 20 сот. Дізнаємося, скільки сотень залишилося поділити. Віднімемо 20 сот. від 21 сот., отримаємо 1 сот. 1 менше від 4. Отже, цифра 5 правильна.
Утворимо друге неповне ділене. Замінимо сотню десятками, отримаємо 10 дес; додамо 4 дес. діленого, отримаємо 14 дес. 14 дес. поділимо на 4, буде З дес. Визначимо, скільки всього десятків поділили. Помножимо 3 дес. на 4, отримаємо 12 дес. Дізнаємося, скільки десятків залишилося поділити. Піднімемо 12 дес. від 14 дес, отримаємо 2 дес.
Утворимо третє неповне ділене. Замінимо 2 дес. одиницями, отримаємо 20 од.; додамо 8 од. діленого, отримаємо 28 од. 28 од. поділимо на 4, буде 7. Визначимо, скільки одиниць поділили. Помножимо 7 од. на 4, отримаємо210 Розділ IX. Нумерація багатоцифрових чисел і арифметичні дії в межах мільйона
; Подамо на цьому самому прикладі зразок короткого пояснення.
Ділене 2 148, дільник 4. Перше неповне ділене 21 сот., тому в частці отримаємо трицифрове число. 21 поділимо на 4, буде 5. Поділили 20 сот. Залишилася 1 сот.
Друге неповне ділене 14 дес. Поділимо на 4, буде 3 дес. Поділили 12 дес. (Залишилося 2 дес.
Третє неповне ділене 28 од. Поділимо на 4, буде 7 од. «■■ Частка 537.
; Слід звернути особливу увагу на випадки ділення, коли в результаті отримуємо нулі в кінці або всередині частки. Щоб учні не пропускали нулі в частці, треба привчити їх ще до виконання ділення за назвою першого неповного діленого визначати кількість цифр у частці.
Треба домогтися усвідомлення ними, що процес знаходження кожної з цифр частки складається з таких операцій: а) утворення неповного діленого; б) знаходження відповідної цифри частки; в) знаходження числа одиниць відповідного розряду, які поділили; г) знаходження числа одиниць цього розряду, що залишилися неподіленими, і визначення за остачею правильності дібраної цифри частки.
Відповідно до цього будується загальна пам’ятка. На одному з уроків варто порівняти неповні ділені з відповідними зручними доданками.
Якщо знайдемо зручні доданки, то можна виконати ділення усно. 741 : 3 = (600 + 120 + 21) : 3 = 200 + 40 + 7 = 247.
(Зручними доданками є такі числа, від ділення яких на дільник отримуємо розрядні доданки частки).
Складене іменоване число при діленні на одно- або двоцифрове число замінюють на просте. Якщо ділене і дільник — іменовані числа, то їх треба подати простими іменованими числами в однакових одиницях.
56 грн. 22 коп. : 6 = 9 грн. 37 коп. 20 т 025 кг : 5 кг = 4 005
56 грн. 22 коп. = 5 622 коп. 20 т 025 кг = 20 025 кг
Окремо потрібно розглянути випадок ділення, коли при діленні залишається остача і в кінці частки треба дописати нуль. Такі вирази учні обчислюють під керівництвом вчителя.

Множення на розрядні числа. У методичній літературі часто не звертається увага на відмінність понять «круглі числа» і «розрядні числа». Відповідно нечітко розрізняють і такі твердження, як «множення на круглі числа» і «множення на розрядні числа». Круглі числа — це будь-які числа, що закінчуються нулями (4 700, 800, 120, 80, 5 000). Розрядні числа — це числа, що містять лише одну значущу цифру (6, 40, 800, 3 000).
Перші уроки використовують для повторення переставної і сполучної властивостей дії множення, розглядають множення числа на добуток та множення на 10, 100 і 1 000. Виконують також вправи на подання розрядних чисел у вигляді добутків, де один з множників буде число виду 10, 100, 1 000 і т. д. (600 = 6 • 100; 8 000 = 8 • 1 000).
Варто також опрацювати з учнями такі вправи: >1. Розгляньте записи і поясніть різні способи обчислення значень виразів.
17 • (2 ■ 3) = 17 • 6 = 102;
17 — (2 — 3) = (17 • 2) • 3 = 34 — 3 = 102;
17 • (2 • 3) = (17 • 3) — 2 = 51 • 2 = 102.
Після виконання вправи подамо правило множення числа на добуток: щоб помножити число на добуток, можна знайти добуток і помножити число на знайдений результат, а можна помножити це число на один з множників і знайдений результат помножити на інший множник.
2. За зразком кожне з розрядних чисел 20, 400 і 9 000 подайте у вигляді добутку. Зразок. 50 000 = 5 • 10 000.
3. Знайдіть добуток (усно).
5-Ю 12-100 50-1000
4. Запишіть друге число у вигляді зручних множників і знайдіть добутки. 15 -20 24 • 30 20 • 20
Зразок. 15 • 40 = 15 • (4 • 10) = (15 • 4) • 10 = 60 • 10 — 600.
5. Порівняйте обчислення за правилами множення числа на добуток і числа на суму.
7 • 80 = 7 • (8 • 10) = (7 • 8) • 10 = 560;
7 • 18 = 7 • (10 + 8) = 7 • 10 + 7 • 8 = 70 + 56 = 126.
Тема «Множення чисел на розрядні числа».
Бесіда. Розв’яжемо задачу: «На фермі від корів за день надоїли 300 бідонів молока по 34л у кожному. Скільки літрів молока надоїли на фермі?’.
Обчислення виконаємо усно.
34 • 300 = 34 • (3 • 100) = (34 • 3) • 100 = 102 • 100 = 102 000 (л).
Із запису випливає, що спочатку число 34 треба було помножити на З, а потім дописати два нулі. З урахуванням цього і робимо письмовий запис: значущу цифру 3 записуємо під одиницями першого множника і множимо 34 на 3, а потім до знайденого добутку допишемо справа два нулі.
102 00212 Розділ IX. Нумерація багатоцифрових чисел і арифметичні дії в межах мільйона
У процесі закріплення матеріалу на наступних уроках розглядають випадки, в яких обидва множники закінчуються нулями. При цьому множники записують так:
Після розв’язування кількох таких прикладів роблять висновок: якщо множники закінчуються нулями, то множать, не звертаючи уваги на ці нулі, а потім до добутку дописують стільки нулів, скільки їх в кінці обох множників разом.
Ділення на розрядні числа. Вивчення ділення на розрядні числа базується на властивості ділення числа на добуток. На основі цієї властивості розкривають спосіб послідовного ділення. Треба також повторити ділення на 10, 100 і 1000 без остачі та розглянути ділення на ці числа з остачею.
Повторюють властивість ділення числа на добуток, виконуючи такі вправи:
1. Поясніть різні способи обчислення виразів. 24: (3-4) = 24: 12 = 2,
24 : (3 ■ 4) = (24 : 3) : 4 = 8 : 4 = 2, 24 : (3 • 4) = (24 : 4) : 3 = 6 : 3 = 2.
2. Знайдіть значення виразів зручним способом: 80: (2 -8) 300: (10-2) 24 : (3 • 7)
3. Знайдіть частку, розкладаючи дільник на зручні множники. 320:40 (320: 40 = 320: (4- 10) = . ).
З діленням на 10, 100 і 1 000 з остачею ознайомлюють учнів методом бесіди. Нехай треба 67 поділити на 10. Виділіть уділеному найбільше число, що ділиться на 10 без остачі. Це число 60; поділимо його на 10, отримаємо 6, 7 од. становитимуть остачу.
67 : 10 = 6 (ост. 7). .:
Розгляньте записи і поясніть розв’язання.
874 : 100 = 8 (ост. 74); 4 500 : 1 000 = 4 (ост. 500).
При вивченні ділення на розрядні числа особливо грунтовно треба опрацювати ділення трицифрового числа на круглі десятки (без остачі і з остачею). Ця операція є основною складовою алгоритму ділення багатоцифрового числа на двоцифрове.
Письмове ділення трицифрового числа на круглі десятки (з остачею) опрацьовують на основі коментованого розв’язування прикладів самим вчителем.
Щоб поділити 294 на 40, треба спочатку поділити це число на 10. Буде 29. Потім поділимо 29 на 4. Візьмемо по 7. 294 [40 Дізнаємося, яке число поділили. Помножимо 40 на 7, буде 280. 280 |7 Дізнаємося, скільки залишилося поділити. 294 мінус 280, буде 14 14. Залишилося 14. Частка 7, остача 14.
45780 420 378 360 180 180 0
Наступний урок слід присвятити закріпленню навичок ділення на круглі десятки, поступово скорочуючи пояснення. Про ділення на 10 не говорять, а ділять подумки: щоб поділити 294 на 40, достатньо 29 поділити на 4.
Тема «Ділення багатоцифрового числа на круглі десятки (загальний випадок)».
Пояснення. Треба поділити 45 780 на 60. Перше неповне ділене 457 сот. Отже, вищим розрядом частки будуть сотні. У частці буде 3 цифри. Знайдемо першу цифру частки. Для цього 457 сот. поділимо на 10 і одержане число 45 поділимо на 6, буде 7 сот. Дізнаємося, скільки сотень поділили. Для цього 60 помножимо на 7, буде 420. Дізнаємося, скільки сотень не поділили. 457 мінус 420, буде 37. 37 менше, ніж 60. Цифру 7 знайдено правильно.
Утворимо друге неповне ділене. 37 сот. — це 370 дес. І ще 8 дес. діленого, буде 378 дес. Знайдемо другу цифру частки. Для цього достатньо 37 поділити на 6, буде 6. Дізнаємося, скільки десятків поділили. 60 помножимо на 6, буде 360. Дізнаємося, скільки десятків не поділили. 378 мінус 360, буде 18. 18 менше, ніж 60. Цифру 6 знайдено правильно.
Утворимо третє неповне ділене. 18 дес. — це 180 од. Окремих одиниць нема, тому третім неповним діленим буде 180 од. Знайдемо третю цифру частки. Для цього достатньо поділити 18 на 6, буде 3. В остачі 0. Частка — 763.
Аналогічно пояснюють ділення багатоцифрового числа на круглі десятки, коли в частці з’являються нулі, та ділення на трицифрове розрядне число.
Множення на дво- і трицифрові числа. Передумовою для успішного вивчення множення на двоцифрове число є вміння учнів виконувати письмове множення на одноцифрове число та розрядні числа. Теоретична основа множення на двоцифрове нерозрядне число — властивість множення числа на суму.
Опрацювання матеріалу розпочинають з множення двоцифрового числа на двоцифрове. (На початку навчального року учні 4 класу вже розглядали цей випадок у межах 1 000).
Учням пропонують прочитати пояснення про усний і письмовий способи знаходження добутку чисел 32 і 36.
Усно. 32 • 36 = 32 • (ЗО + 6) = 32 • 30 + 32 • 6 = 960 + 192 = 1 152. .
Із цього запису видно, що для знаходження результату множення на двоцифрове число треба перший множник окремо помножити на десятки й одиниці і результати додати.
На основі переставної властивості дії додавання можна спочатку помножити число на одиниці, а потім на десятки. Так роблять при письмовому множенні. 214
Розділ IX. Нумерація багатоцифрових чисел- і арифметичні дії в межах Письмово.
При письмовому множенні множники розміщують так, щоб одиниці були записані під одиницями. Множення розпочинають з одиниць. При множенні на десятки цифри другого неповного добутку починають записувати під десятками. Останньою дією знаходять суму неповних добутків. Учитель пропонує учням прочитати спочатку перший неповний добуток, а тоді другий неповний добуток (96 дес).
Множення на трицифрове число з усіма розрядами не викликає труднощів. Для введення нового виду множення доцільно розглянути два схожих добутки, наприклад: 373 • 47 і 373 • 247.
Спостереження показують, що в окремих учнів виникають труднощі при множенні чисел, які містять нулі. Для запобігання помилкам застосовують коментоване розв’язування. Подамо зразок коментування.
Спочатку 3 054 множимо на 4 одиниці і в результаті отримуємо одиниці. Результат цього множення починаємо записувати під одиницями: 4 на 4, буде 16, пишемо 6, 1 запам’ятовуємо; 5 на 4, буде 20 і ще 1, буде 21, пишемо 1, а 2 запам’ятовуємо; 0 на 4, буде 0 і ще 2, пишемо 2; 3 на 4, буде 12, записуємо 12.
У числі 204 — 0 десятків. Тому 3 054 будемо відразу множити на 2 сот. І в результаті отримаємо сотні. Результат цього множення починаємо * записувати під сотнями: 4 на 2, буде 8, цифру 8 записуємо на місці сотень; 5 на 2, буде 10, 0 пишемо, 1 запам’ятовуємо і т. д. Маємо два неповних добутки: перший неповний добуток — 12 216, другий неповний добуток — 6 108 сот. Добуток — 623 016.
Ділення багатоцифрового числа на двоцифрове. Спочатку розглядають ділення трицифрового числа (без остачі і з остачею) на двоцифрове з одноцифровою часткою, звернувши увагу на спосіб знаходження цифри частки.
Пояснення. Розгляньмо вираз на ділення трицифрового числа на двоцифрове з остачею.
Ділене 752, дільник 86. Цифру частки будемо добирати, а потім випробовувати. Щоб легше було добирати, замінимо дільник меншим розрядним числом. Це буде 80. Поділимо 752 на 80; для цього достатньо 75 поділити на 8, буде 9. Перевіряємо усно число 9. 80 помножити на 9, буде 720 та ще 6 помножити на 9, буде 54, разом більше, ніж 752. Цифра 9 не підходить. Візьмемо число 8. 80 помножити на 8, буде 640 та ще 6 помножити на 8, буде 48, разом 688. 688 менше, ніж 752. Цифра 8 підходить. Запишемо її в частку. Знайдемо, скільки одиниць залишилося поділити.
752 відняти 688, буде 64. Частка 8, остача 64.
12216 6108 623016
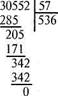
Тема «Ділення багатоцифрового числа на двоцифрове (загальний випадок)».
Перше неповне ділене 305 сот. Отже, вищим розрядом частки будуть сотні. У частці буде 3 цифри. Будемо шукати першу цифру частки. Поділимо 30 на 5, буде 6. Перевіряємо число 6 усно. 50 помножити на 6, буде 300 та ще 7 помножити на 6, разом буде більше, ніж 305. Отже, цифра 6 не підходить. Візьмемо число 5. Перевіримо його. 57 помножити на 5, буде 285. 285 менше, ніж 305, тому цифра 5 підходить. Запишемо її в частку. Віднімемо 285 від 305, буде 20. Аналогічно знаходимо другу і третю цифри частки.
З учнями треба грунтовно опрацювати випадки ділення, коли частка містить нуль. Розгляньмо такі вирази.
Пояснення. Перше неповне ділене 245 сот. Отже, вищим розрядом частки будуть сотні. У частці буде 3 цифри. Визначимо першу цифру частки. Для цього поділимо 24 на 6, буде 4. 61 помножимо на 4, буде 244. Від 245 відняти 244, буде 1 (сотня).
Друге неповне ділене 18 дес. 18 дес. не можна поділити на 24583161 61 так, щоб отримати десятки. Тому в частці на місці десятків 244 пишемо нуль. 183′
Третє неповне ділене 183 од. Визначимо третю цифру частки 183
У цьому прикладі останнє (четверте) неповне ділене — 310 |5220 нуль одиниць. 0 поділити на 62, буде 0. На місці одиниць у 136 частці записуємо 0. 124
У цьому прикладі третє неповне ділене — 8 одиниць. 8 не
ділиться на 64. Отже, в частку на місці одиниць записуємо 0, а -тт> І
8 — це остача. РОЗДІЛ X
У початкових класах розглядають як скалярні величини (довжина, площа, маса, місткість, час, вартість, ціна тощо), так і векторну величину (швидкість).
Ви’вчення величин — це один із засобів зв’язку навчання математики з життям. Ознайомлення учнів з величинами та одиницями їх вимірювання і формування відповідних умінь і навичок здійснюється у тісному зв’язку з формуванням поняття натурального числа, з вивченням арифметичних дій над числами, з формуванням поняття геометричної фігури. Вивчення величин і одиниць їх вимірювання треба організувати так, щоб діти набули деяких практичних навичок вимірювання величин, конкретно уявляли одиниці їх вимірювання та співвідношення між ними.
Дата добавления: 2015-04-18 ; просмотров: 139 ; Нарушение авторских прав
lektsii.com
