Справочник химика 21

Химия и химическая технология

Правило креста

Для разбавления концентрированной серной кислоты удобно пользоваться правилом креста . Для этого требуемую концентрацию раствора пишут в месте пересечения двух линий (в центре креста ), концентрацию исходной серной кислоты — у левого верхнего конца одной из этих линий, а концентрацию воды, равную нулю, — у левого нижнего конца другой линии пересечения. На каждой линии проводится вычитание чисел, и разность записывается у свободного конца той же линии. Полученные числа справа вверху и внизу указывают, сколько следует взять весовых частей серной кислоты и воды, чтобы получить требуемую концентрацию раствора в реакторе. Например, для 83%-ной серной кислоты правило креста строится следующим образом [c.41]

Правило креста можно применять и в случаях разбавления раствора чистым растворителем. При этом концентрацию вещества в чистом растворителе считают равной нулю [c.50]

Правило креста)). Расчеты разбавления и смешения двух растворов или других веществ удобно производить с помощью так называемого креста , представляющего собой две пересекающиеся прямые [c.21]

Правило смешения ( правило креста ) применяется для упрощения расчетов в случае приготовления раствора заданной концентрации (в вес. %) путем разбавления растворителем или смешением двух растворов (пп. 2 и 4). [c.347]

Решаем задачу с помош ью правила креста . [c.180]

Правило креста . Расчеты при разбавлении и смешении двух растворов или других веществ удобно производить [c.17]

При решении задач на смешивание и разбавление растворов широко применяют такие известные приемы, как правило креста , решение квадрата Пирсона, решение посредством диагональных схем и т.д. [c.167]

Решение. Чтобы узнать, в каких количествах необходимо взять два раствора данного вещества известной концентрации для приготовления его раствора требуемой концентрации, сначала вычисляют, в каком отношении нужно смешать данные растворы затем требуемое количество делят пропорционально вычисленному отношению. Для решения первого вопроса применяют так называемое правило с.чешения ( правило креста или правило квадрата ), [c.34]

Применение правила креста рассмотрим на следующих примерах. [c.28]

Эту задачу можно решить, используя правило смешения (правило креста ). [c.135]

Второй способ расчета. Этот способ известен под названием правило креста из-за внешнего вида схематического оформления расчета [c.59]

Выведите формулу для расчета задач типа В каком весовом соотношении нужнО смешать Л%-ный и В%-ный растворы некоторого вещества для получения С%-ного раствора Иными словами, дайте математическое обоснование правила креста . [c.30]

Уравнение (4) — математическое выражение правила (закона) смешивания для вычисления соотношений, в которых следует брать исходные растворы для получения раствора с заданной массовой долей растворенного вещества. При вычислении соотношений, в которых следует смешивать два раствора, используют так называемое правило креста или находят их с помощью диагональной схемы. Схему решения задач этим способом можно представить следующим образом [c.169]

Правило смешения ( правило креста ) [c.45]

Правило смешения ( правило креста ). 45 [c.1180]

Применение правила креста для приготовления растворов заданной концентрации или плотности поясняется следующими ниже примерами [c.676]

Это ясно априори и наглядно иллюстрирует применение правила креста ). [c.21]

Для расчетов возможно также использовать правило креста или диагоналей (см. выше). [c.23]

Используя правило креста , определите, в каком объемном отношении [c.19]

Применяя правило креста, получим [c.26]

Задачу можно решить посредством правила креста . В точке пересечения двух прямых обозначают массовую долю раствора серной кислоты в смеси, слева у концов прямых от точки пересечения указывают массовые доли составных частей смеси, а справа указывают разности массовых долей смеси и ее составных частей. Для решения данной задачи схема имеет вид [c.172]

Примечание Эту задачу можно решить с помощью правила креста . [c.127]

Правило смешения ( Правило креста ) [c.74]

Такой же результат можно получить, используя правило креста . В центре пишут искомую концентрацию. Слева данные величины. По диагонали из большей величины вычитают меньшую и спра- 2 д ва получают искомые величины, т. е. со- И отношение, в котором нужно взять исход- 5 °° 10 ные растворы, чтобы получить раствор нужной концентрации. Это соотношение сохраняется для данных исходных растворов, независимо от того, какое весовое количество щелочи надо приготовить. В соответствии со схемой нужно взять 5 вес. ч. 20%-ного раствора и 10 вес. ч. 5%-ного раствора, или в соотношении [c.29]

Такой же результат можно получить, используя правило креста . В центре пишут искомую концентрацию, слева — данные величины. По диагонали из большей величины вычитают меньшую и справа получают искомые величины, т. е. соотношение, в котором надо взять искомые величины, чтобы получить раствор нужной концентрации [c.22]

Примечание. Применение правила креста для растворов с заданной плотностью допустимо только в том сл> чае, если плотность растворов линейно изменяется с изменением концентрации, что не всегда соблюдается (см., например, раствор аммиака и уксусной кислоты). [c.676]

Следовательно, нужно взять 30 мае. ч. 90-процентного раствора и прилить к ним 50 мае. ч. 10-процентного раствора. Если написать правило креста в общем виде, то схема будет такова [c.310]

Решение. Из правила креста следует, что на 1 вес. ч. 20%-ного раствора нужно взять 2 вес. ч. 5%-ного раствора (см. выше). Получается 3 вес. ч. 10%-ного раствора. Исходя из того, что на приготовление 3 кг 10%-ного раствора щелочи требуется 2/сз 5%-ного раствора, найдем, сколько потребуется 5%-ного раствора для приготовления 2 кг 10%-ного раствора [c.30]

Для нриготовлепия олеума смешением более концентрированного с менее концентрированным используют правило креста нлн расчет по балансу свободного SO3. [c.57]

В данном случае целесообразно использовать графический прием правило креста . [c.309]

Смотреть страницы где упоминается термин Правило креста: [c.24] [c.676] [c.18] [c.160] [c.147] [c.94] [c.391] Смотреть главы в:

Производство серной кислоты Издание 3 (1967) — [ c.259 ]

Технология серной кислоты (1956) — [ c.205 ]

Техника лабораторных работ (1982) — [ c.108 , c.109 ]

Производство серной кислоты Издание 2 (1964) — [ c.259 ]

Химия и технология ароматических соединений в задачах и упражнениях (1971) — [ c.63 ]

Производство серной кислоты (1956) — [ c.205 ]

Технология серной кислоты (1971) — [ c.261 , c.262 ]

Производство серной кислоты (1968) — [ c.263 ]

chem21.info

Основные методы решения задач на смешивание растворов

“Только из союза двоих, работающих вместе и при помощи друг друга, рождаются великие вещи.”

Антуан Де Сент-Экзюпери

Математика многообразна и многогранна. Существует ряд ситуаций в образовательном процессе, когда при изучении какой-либо темы по физике, химии, биологии и т.д. затрагиваются понятия математики, например, существуют задачи, которые решают как на уроках математики, так и на уроках химии. Способы решения задач представляют и учителя химии, и математики, но есть проблема: математики знают математику, а химики — химию. И не всегда способы совпадают.

В данной статье приводятся рекомендации по решению химических задач на смешение растворов разными способами: с помощью расчетной формулы, “Правила смешения”, “Правила креста”, графического метода, алгебраического метода. Приведены примеры решения задач.

1. Основные химические понятия

Приведем некоторые указания к решению задач на растворы.

Основными компонентами этого типа задач являются:

а) массовая доля растворенного вещества в растворе;

б) масса растворенного вещества в растворе;

в) масса раствора.

а) все получившиеся смеси и сплавы являются однородными;

б) смешивание различных растворов происходит мгновенно;

в) объем смеси равен сумме объемов смешиваемых растворов;

г) объемы растворов и массы сплавов не могут быть отрицательными.

Определения и обозначения.

Массовая доля растворенного вещества в растворе — это отношение массы этого вещества к массе раствора.

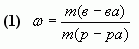
где 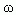— массовая доля растворенного вещества в растворе;

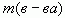— масса растворенного вещества в растворе;

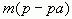— масса раствора.

Следствия формулы (1):

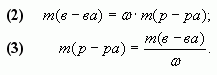
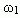— массовая доля растворенного вещества в первом растворе;

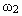— массовая доля растворенного вещества во втором растворе;

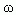— массовая доля растворенного вещества в новом растворе, полученном при смешивании первого и второго растворов;

m₁(в-ва), m₂(в-ва), m(в-ва) — массы растворенных веществ в соответствующих растворах;

m₁(р-ра), m₂(р-ра), m(р-ра) — массы соответствующих растворов.

Основными методами решения задач на смешивание растворов являются: с помощью расчетной формулы, “Правило смешения”, “Правило креста”, графический метод, алгебраический метод.

Приведем описание указанных методов.

1.1. С помощью расчетной формулы

В наших обозначениях, получим формулу для вычисления массовой доли вещества (?) в смеси.

1. Масса полученного при смешивании раствора равна:

2. Определим массы растворенных веществ в первом и втором растворах:

m₁(в-ва)= 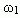•m₁(р-ра), m₂(в-ва)= 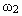•m₂(р-ра).

3. Следовательно, масса растворенного вещества в полученном растворе вычисляется как сумма масс веществ в исходных растворах:

m(в-ва) = m₁(в-ва) + m₂(в-ва) = 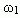•m₁(р-ра) + 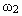•m₂(р-ра).

4. Таким образом, массовая доля растворенного вещества в полученном растворе равна:

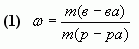
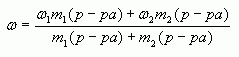
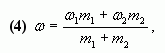
где — массы соответствующих растворов.

Замечание: При решении задач удобно составлять следующую таблицу.

Смесь двух растворов

Массовая доля растворенного вещества

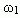
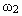
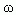
Масса вещества в растворе

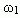m₁

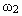m₂

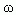(m₁ + m₂)

1.2. “Правило смешения”

Воспользуемся формулой (4):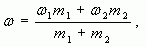

тогда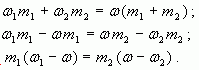

Отсюда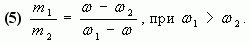

Таким образом, отношение массы первого раствора к массе второго равно отношению разности массовых долей смеси и второго раствора к разности массовых долей первого раствора и смеси.

Аналогично получаем, что при

Замечание: Формула (5) удобна тем, что на практике, как правило, массы веществ не отвешиваются, а берутся в определенном отношении.

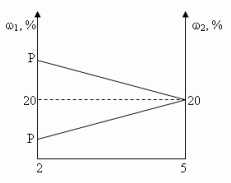
1.3. “Правило креста”

“Правилом креста” называют диагональную схему правила смешения для случаев с двумя растворами.

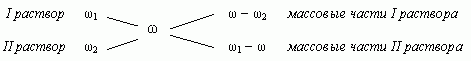
Слева на концах отрезков записывают исходные массовые доли растворов (обычно слева вверху-большая), на пересечении отрезков — заданная, а справа на их концах записываются разности между исходными и заданной массовыми долями. Получаемые массовые части показывают в каком отношении надо слить исходные растворы.

1.4. Графический метод

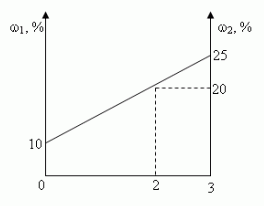
Отрезок прямой (основание графика) представляет собой массу смеси, а на осях ординат откладывают точки, соответствующие массовым долям растворенного вещества в исходных растворах. Соединив прямой точки на осях ординат, получают прямую, которая отображает функциональную зависимость массовой доли растворенного вещества в смеси от массы смешанных растворов в обратной пропорциональной зависимости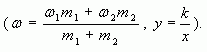

Полученная функциональная прямая позволяет решать задачи по определению массы смешанных растворов и обратные, по массе смешанных растворов находить массовую долю полученной смеси.

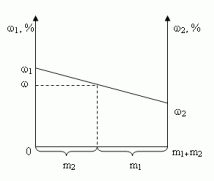
Построим график зависимости массовой доли растворенного вещества от массы смешанных растворов. На одной из осей ординат откладывают точку, соответствующую массовой доли 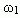, а на другой — 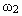. Обозначим на оси абсцисс точки А и В с координатами (0,0) и (m₁ + m₂,0), соответственно. На графике точка А(0,0) показывает, что массовая доля всего раствора равна 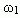, а точка В(m₁ + m₂,0) — массовая доля всего раствора равна 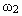. В направлении от точки А к точке В возрастает содержание в смеси 2-го раствора от 0 до m₁+ m₂ и убывает содержание 1-го раствора от m₁+ m₂ до 0. Таким образом, любая точка на отрезке АВ будет представлять собой смесь, имеющую одну и ту же массу с определенным содержанием каждого раствора, которое влияет на массовую долю растворенного вещества в смеси.

Замечание: Данный способ является наглядным и дает приближенное решение. При использовании миллиметровой бумаги можно получить достаточно точный ответ.

1.5. Алгебраический метод

Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений.

2. Примеры решения задач

В 100 г 20%-ного раствора соли добавили 300 г её 10%-ного раствора. Определите процентную концентрацию раствора.

Решение:

C помощью расчетной формулы

Путем последовательных вычислений

Сколько растворенного вещества содержится:

а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]

б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]

Сколько вещества содержится в образовавшемся растворе?

20 г + 30 г = 50 г

Чему равна масса образовавшегося раствора?

100 г + 300 г = 400 г

Какова процентная концентрация полученного раствора?

Пусть х — процентная концентрация полученного раствора. В первом растворе содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в полученном растворе х•(100 + 300)(г) соли. Составим уравнение:

0,2•100 + 0,1•300 = х•(100 + 300);

Задача 2. u(№10.26, [1])

Смешали 10%-ный и 25%-ный растворы соли и получили 3 кг 20%-ного раствора. Какое количество каждого раствора в килограммах было использовано?

а) C помощью уравнения:

Пусть х (кг) — масса 1-го раствора, тогда 3-х (кг) -масса 2-го раствора.

0,1•х (кг) содержится соли в 1-ом растворе,

0,25•(3-х) (кг) содержится соли в 2-ом растворе,

0,2•3 (кг) содержится соли в смеси.

Учитывая, что масса соли в 1-ом и 2-ом растворах равна массе соли в смеси, составим и решим уравнение:

0,1•х + 0,25•(3-х) = 0,2•3;

х = 1, 1кг-масса 1-го раствора

3 — х = 3 — 1 =2 (кг) — масса 2-го раствора.

б) С помощью системы уравнений

Пусть х (кг) — количество первого раствора, у (кг) — количество второго раствора. Система уравнений имеет вид:

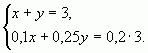
Ответ: 1 кг, 2 кг.

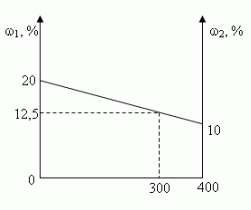
Составим диагональную схему

Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму) раствора соли. Сколько литров 20%-ного раствора такой же соли надо налить в сосуд, чтобы процентное содержание соли в сосуде стало наибольшим?

Решение (графический способ)

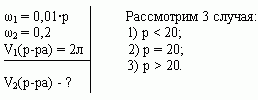
Заметим, что по условию, объём второго раствора не превышает трёх литров.

1. Ели р 20, то при добавлении 2-го раствора, процентное содержание соли будет уменьшаться, т.е. прилить нужно 0 л.

xn--i1abbnckbmcl9fb.xn--p1ai

Методика решения задач
на растворы с применением
правила креста

Многие важные вопросы изучения курса химии по ряду причин исключены из школьной программы. Среди них закон эквивалентов, разные способы выражения концентрации растворов, правило креста и многие другие. Однако на факультативных занятиях, при подготовке ребят к олимпиадам без них не обойтись. Да и в жизни ребятам они пригодятся, особенно тем, кто свяжет будущую профессию с химией (заводские лаборатории, аптеки, научно-исследовательская работа, да и просто химия в быту).
Особенно трудно в этом отношении молодым учителям – у них нет той массы дополнительной литературы, которую накопили старые учителя за десятки лет работы в школе, а что издает современная книгопечатная отрасль промышленности – известно всем. Поэтому предлагаемая методика решения задач на растворы с применением правила креста, думается, хоть сколько-то поможет молодым коллегам в этом деле.

«Конверт Пирсона»

Очень часто в лабораторной практике и при решении олимпиадных задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчет. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «конверта Пирсона», или, что то же самое, правило креста).
Допустим, нужно приготовить раствор определенной концентрации, имея в распоряжении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m₁, а второго – через m₂, то при смешивании общая масса смеси будет слагаться из суммы этих масс. Пусть массовая доля растворенного вещества в первом растворе – ₁, во втором – ₂, а в их смеси – ₃. Тогда общая масса растворенного вещества в смеси будет слагаться из масс растворенного вещества в исходных растворах:

m₁•₁ + m₂•₂ = ₃(m₁ + m₂₎.

m₁(₁ – ₃) = m₂(₃ – ₂),

m₁/m₂ = (₃ – ₂)/(₁ – ₃).

Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешении. При расчетах записывают одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

Для пояснения этого правила сначала решим простейшую задачу.

ЗАДАЧА 1

Определите концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10%-го растворов какой-либо соли.

Дано:

m₁ = 150 г,
m₂ = 250 г,
₁ = 30%,
₂ = 10%.

Найти:

1-й способ (метод пропорций).

Общая масса раствора:

Массу вещества в первом растворе находим методом пропорций, исходя из определения: процентная концентрация раствора показывает, сколько граммов растворенного вещества находится в 100 г раствора:

100 г 30%-го р-ра – 30 г в-ва,

150 г 30%-го р-ра – х г в-ва,

х = 150•30/100 = 45 г.

Для второго раствора составляем аналогичную пропорцию:

100 г 10%-го р-ра – 10 г в-ва,

250 г 10%-го р-ра – y г в-ва,

y = 250•10/100 = 25 г.

Следовательно, 400 г нового раствора содержит 45 + 25 = 70 г растворенного вещества.

Теперь можно определить концентрацию нового раствора:

400 г р-ра – 70 г в-ва,

100 г р-ра – z г в-ва,

z = 100•70/400 = 17,5 г, или 17,5%.

2-й способ (алгебраический).

m₁•₁ + m₂•₂ = ₃(m₁ + m₂).

₃ = (m₁•₁ + m₂•₂)/(m₁ + m₂).

В результате находим:

₃ = (150•30 + 250•10)/(150 + 250) = 17,5%.

3-й способ (правило креста).

(₃ – 10)/(30 – ₃) = 150/250.

(30 – ₃)•150 = (₃ – 10)•250,

4500 – 150₃ = 250₃ – 2500,

4500 – 2500 = 250₃ – 150₃,

7000 = 400₃, ₃ = 7000/400 = 17,5%.

Ответ. При слиянии взятых растворов получится новый раствор с концентрацией ₃ = 17,5%.

Теперь решим задачи посложнее.

ЗАДАЧА 2

Определите, сколько нужно взять 10%-го раствора соли и 30%-го раствора этой же соли для приготовления 500 г 20%-го раствора.

₁ = 10%,
₂ = 30%,
₃ = 20%,
m₃ = 500 г.

Используем правило креста.

Для приготовления 500 г 20%-го раствора соли нужно взять по 10 частей растворов исходных концентраций.
Проверим правильность нашего решения, учитывая, что 1 часть равна 500/(10 + 10) = 25 г.

250 г 10%-го р-ра – х г соли,

100 г 10%-го р-ра – 10 г соли,

х = 250•10/100 = 25 г.

250 г 30%-го р-ра – y г соли,

100 г 30%-го р-ра – 30 г соли,

y = 250•30/100 = 75 г.

m(р-ра) = 250 + 250 = 500 г.

m(соли) = 25 + 75 = 100 г.

Отсюда находим ₃:

500 г р-ра – 100 г соли,

100 г р-ра – ₃ г соли,

₃ = 100•100/500 = 20 г, или 20%.

Ответ. Для приготовления 500 г 20%-го раствора нужно взять исходные растворы по 250 г
(m₁ = 250 г, m₂ = 250 г).

ЗАДАЧА 3

Определите, сколько нужно взять растворов соли 60%-й и 10%-й концентраций для приготовления 300 г раствора 25%-й концентрации.

Дано:

₁ = 60%,
₂ = 10%,
₃ = 25%,
₃ = 300 г.

Решение

Масса одной части: 300/50 = 6 г.

Проверим правильность решения.

100 г 60%-го р-ра – 60 г соли,

90 г 60%-го р-ра – х г соли,

210 г 30%-го р-ра – y г соли,

m(соли) = 54 + 21 = 75 г.

Находим концентрацию нового раствора:

300 г р-ра – 75 г соли,

100 г р-ра – z г соли,

z = 100•75/300 = 25 г, или 25%.

Теперь перейдем к еще более сложным задачам.

ЗАДАЧА 4

Определите массу раствора Nа₂СО₃ 10%-й концентрации и массу сухого кристаллогидрата Na₂CO₃•10H₂O, которые нужно взять для приготовления 540 г раствора 15%-й концентрации.

Дано:

₁ = 10%,
₃ = 15%,
m₃ = 540 г.

1-й способ (через систему уравнений с двумя неизвестными).

Определяем массу соли Na₂CO₃ в 540 г 15%-го раствора:

100 г 15%-го р-ра – 15 г соли,

540 г 15%-го р-ра – z г соли,

z = 540•15/100 = 81 г.

Cоставляем систему уравнений:

Находим молярную массу:

Избавляемся от лишних неизвестных:

Подставляем m₂ и m₁ в систему уравнений:

С учетом того, что х = 81 – y, избавляемся от второго неизвестного:

Тогда m₂ = 286y/106 = 2,7•37 100 г – это масса необходимого количества кристаллогидрата Na₂СО₃•10H₂O.
Далее находим: х = 81 – y = 81 – 37 = 44 г – это масса соли из 10%-го раствора.
Находим массу 10%-го раствора:

m₁ г 10%-го р-ра – 44 г соли,

Видно, что так можно решить данную задачу – способ надежный, но, к сожалению, достаточно длинный, громоздкий и сложный. Им успешно могут воспользоваться учащиеся с достаточно развитым логическим мышлением. Для других он будет сложноват.

2-й способ (правило креста).

Допустим, что Na₂СО₃•10H₂O – это «сухой раствор» (ведь он же содержит воду). Тогда найдем его «концентрацию»:

286 г – 106 г соли,

100 г – х г соли,

х = 100•106/286 = 37 г, или 37%.

Применяем правило креста.

Находим массу одной части и массы веществ:

Ответ. Для приготовления 540 г раствора Na₂CO₃ 15%-й концентрации необходимо взять 440 г 10%-го раствора и 100 г кристаллогидрата.
Таким образом, применение правила креста удобнее и проще при решении подобных задач. Этот способ более экономичен по времени и менее трудоемок.
Правило креста можно применять и в тех случаях, когда нужно получить раствор меньшей концентрации путем разбавления водой более концентрированного раствора или получить более концентрированный раствор путем добавления к исходному раствору сухой смеси. Рассмотрим это на примерах.

ЗАДАЧА 5

Сколько воды нужно добавить к 250 г раствора соли для понижения его концентрации с 45% до 10%?

₁ = 45%,
₃ = 10%,
m₁ = 250 г.

Найти:

Решение

Принимаем, что концентрация для добавляемой воды – ₂ = 0%. Используем правило креста.

Определяем массу одной части через первый раствор: 250/10 = 25 г.
Тогда масса необходимой воды равна:

Проверим правильность решения.
Масса нового раствора:

250 г 45%-го р-ра – х г соли,

100 г 45%-го р-ра – 45 г соли,

х = 250•45/100 = 112,5 г.

Находим ₃:

1125 г р-ра – 112,5 г соли,

y = 100•112,5/1125 = 10 г, или 10%.

ЗАДАЧА 6

Сколько сухой соли нужно добавить к 250 г раствора 10%-й концентрации для ее увеличения до 45%?

₁ = 10%,
m₁ = 250 г,
₃ = 45%.

Принимаем, что сухая соль – это раствор с ₂ = 100%. Используем правило креста.

Определяем массу одной части через первый раствор: 250/55 = 4,5 г.
Определяем массу сухой соли:

m(с. с.) = 4,5•35 = 158 г.

Проверяем правильность решения.
Масса нового раствора:

Масса соли в исходном растворе:

Общая масса соли в новом растворе:

Концентрация нового раствора:

408 г р-ра – 183 г соли,

100 г р-ра – y г соли,

y = 100•183/408 = 45 г, или 45%.

Ответ. m(с. с.) = 158 г.

Думается, что опытный учитель всегда найдет несколько способов решения любой задачи. Но как учила меня моя первая учительница по химии Клавдия Макаровна в школе № 17 г. Иркутска, так и я стараюсь учить своих учеников: всегда глубоко продумывать и понимать химическую сущность задачи и находить наиболее рациональный способ ее решения, а не просто подгонять под ответ в конце учебника.

him.1september.ru